6.5 NMR Theory and Experiment
Although the other techniques provide valuable information about a molecule, they do not tell us about the overall molecular structure or the framework of C-C and C-H bonds. Nuclear magnetic resonance (NMR) spectroscopy is an immensely powerful analytical technique that provides such information. NMR works by the same principles as a magnetic resonance imaging (MRI) scanner in a hospital. MRI is a scanning technique used to detect hidden medical problems without causing any harm or pain to the patient. While doctors use MRI to peer inside the human body, we will see how NMR allows organic chemists to piece together, atom by atom and bond by bond, the structure of an organic molecule.
NMR-active Nuclei
The basis for NMR is a phenomenon in which some atomic nuclei spin about their axes and as a result generate their own magnetic field or magnetic moment; these nuclei are called NMR-active. Not all nuclei have a magnetic moment though, as only nuclei with an odd number of protons and/or neutrons have one. Fortunately, nuclei that are important for organic compounds, such as the 1H isotope of hydrogen, the 13C isotope of carbon, the 14N isotope of nitrogen, 19F and 31P are all NMR-active and therefore can be observed by NMR. Other nuclei, such as the common 12C isotopes of carbon and 16O isotope of oxygen, do not have magnetic moments and cannot be directly observed by NMR.
In practice, the 1H and 13C nuclei are most commonly observed by NMR spectroscopy, and we will focus on these techniques in this chapter, beginning with 1H NMR. 1H NMR is usually called proton NMR because the nucleus of the 1H atom is actually a single proton. The words ‘proton’ and ‘hydrogen’ will be used interchangeably in this chapter for 1H NMR purposes.
Spin State and Magnetic Resonance
We will take a proton, the nucleus of 1H atom, as an example for the discussions here.
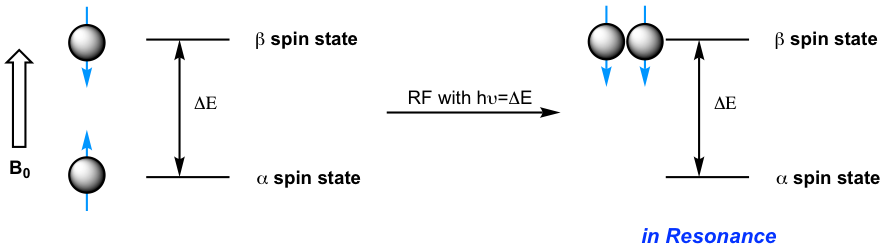
When a sample of an organic compound is sitting in a flask on a laboratory bench, the magnetic moments of all of its protons are oriented randomly. However, when the same sample is placed within the field of a strong magnet in an NMR instrument (this field is referred to as the applied external magnetic field, B0, in NMR), each proton will assume one of two possible orientations with respect to the external magnetic field. These two orientations correspond to the two spin states that can be labelled as α and β. In the α spin state, the proton’s magnetic moment is aligned with the direction of external magnetic field B0, while in the β spin state it is aligned opposed to the direction of B0 (Fig. 6.5b).
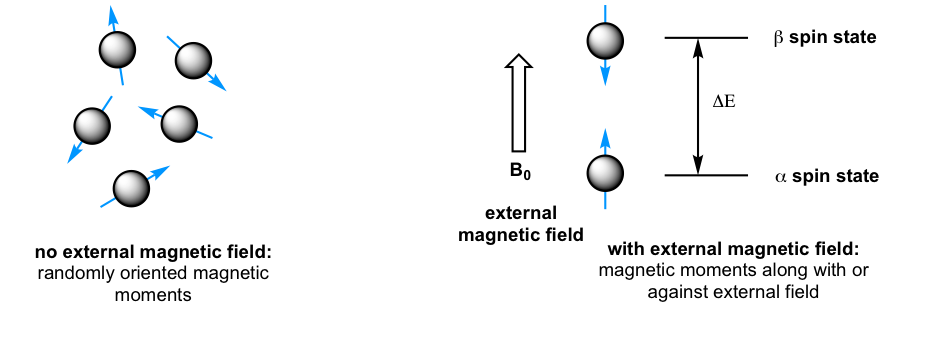
The α spin state is slightly lower in energy than the β state, and the energy gap between them, ΔE, depends upon the strength of B0: a stronger applied external magnetic field results in a larger ΔE. For a large population of organic molecules in an external magnetic field, slightly more than half of the protons will occupy the lower energy α spin state, while slightly less than half will occupy the higher energy β spin state. It is this population difference between the two spin states that is exploited by NMR, and the difference increases with the strength of the applied magnetic field B0.
Energy is required to excite the proton from the lower energy state (α spin state) to the higher energy state (β spin state). In an NMR spectrometer, the energy is supplied by electromagnetic radiation in the radio frequency (RF) region. When a proton in an external magnetic field is exposed to RF radiation with the energy that matches the energy gap ΔE, the energy of the RF is absorbed and the proton will flip its magnetic moment from the lower energy state (α spin state) to the higher energy state (β spin state), and the nuclei are said to be in resonance with the electromagnetic radiation.
The frequency of radiation absorbed by a proton (or any other nucleus) during a spin transition in an NMR experiment is called its resonance frequency, ν. As a result, the resonance frequency also depends on B0; the larger the B0 the higher resonance frequency, and the relationship fits to the specific formula: (Formula 6.4 is for your information purposes only)
γ is the magnetogyric (or gyromagnetic) ratio, and different nuclei have different values of γ. For a proton, the γ value is 26.753 rad · s-1 · tesla-1.
Calculations indicate that if an external magnetic field B0≅1.41 Tesla, the energy difference corresponds to RF with the frequency of 60×106 Hz (60 MHz) for a proton; when B0≅7.04 Tesla, the corresponding RF frequency is 300×106 Hz (300 MHz) for a proton. This frequency is the most important parameter for an NMR spectrometer (the instrument that runs NMR experiments); the higher the frequency, the more sensitive the instrument and the higher resolution the resulting NMR spectrum is.
The NMR Experiment
In this book, we will explain how the NMR experiment and NMR spectrometer work in a simplified way (again with a proton as an example). The full version is outside the scope of this course.
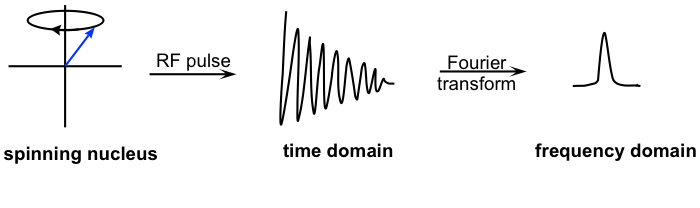
When a sample of a compound is placed in the strong applied external magnetic field B0 of the instrument, the protons begin to spin with one of the two spin states. Initially, slightly more than half of the protons have magnetic moments in a-spin states (aligned with B0), and slightly less than half are in b-spin states (aligned against B0). Then, the sample is exposed to a range of radio frequencies. Out of all of the frequencies that hit the sample, only the frequencies that match the resonance frequency of the protons are absorbed, causing those protons that are aligned with B0 to ‘spin flip’ so that they align themselves against B0. When the ‘flipped’ protons flip back down to their ground state, they emit energy, again in the form of radio-frequency radiation. The NMR instrument detects and records the frequency and intensity of this radiation by making using of a mathematical technique known as a Fourier transform (FT). FT converts the signal from time versus amplitude signals to frequency versus amplitude signals, which is what we observe in an NMR spectrum.
Most modern FT-NMR spectrometers use superconducting magnets that have very high magnetic fields and thus operate with a high resonance frequency from 100 MHz to 800 MHz. Superconducting magnets operate in a bath of liquid nitrogen or liquid helium at a very low temperature.
Despite the high power and resolution of high-frequency NMR spectrometers, the purchase and maintenance of the instrument are very costly. For teaching purposes, the benchtop NMR is becomings more and more popular. The frequency of a benchtop NMR is usually in the range of 60–90 MHz; however, it can provide spectra with good resolution for many basic organic structures used for undergraduate organic chemistry classes. With a low-cost benchtop NMR available, students have the chance to gain hands-on NMR experience in sample preparation, instrument operation and spectrum processing.
Shielding and Deshielding
If all hydrogen atoms (and protons) in organic molecules had the same resonance frequency, then they would all show the same signal, and NMR spectroscopy would not be that useful for chemists. Fortunately, resonance frequencies are different for different protons in a molecule. Specifically, the resonance frequency varies according to the electronic environment a given proton inhabits.
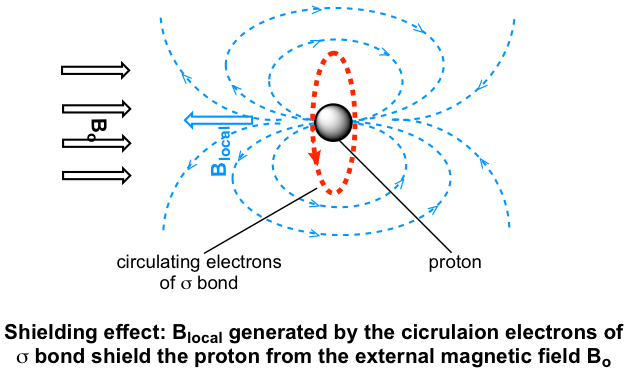
For hydrogen atoms in any bonds, such as C-H, O-H, etc., the external magnetic field B0 causes the s electrons to circulate in a way that generates an induced local magnetic field (Blocal) at the proton, and the direction of the local field Blocal is opposite to the external field B0. The proton thus experiences a net magnetic field, which is called Beff that is smaller than the applied magnetic field:
Beff= B0 – Blocal
As a result, the proton responds to a lower frequency (resonance frequency is proportional to the magnetic field as mentioned earlier). This Blocal, to a small but significant degree, shields the proton from experiencing the full force of B0, so this effect is called the shielding effect. Different hydrogen atoms in organic structures are in different electronic environments and have different electron densities, and so they have different Blocal and different Beff as well. That is why different hydrogens (and protons) are in a different resonance frequency and show different signals in the spectrum.
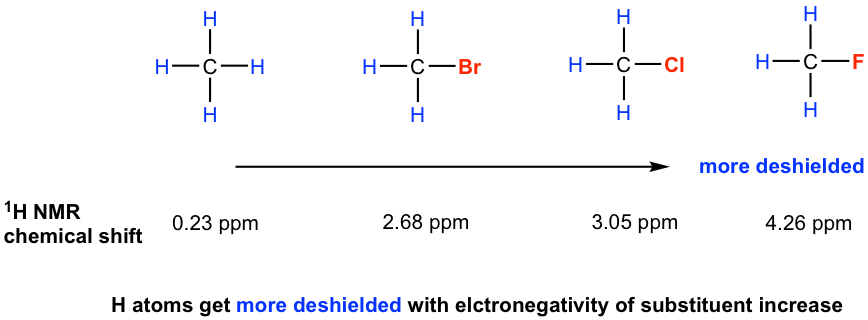
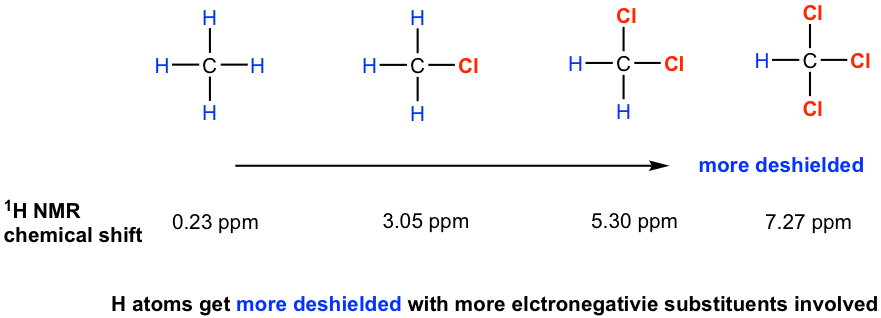
For hydrogen atoms close to electronegative groups, electronegative groups withdraw electron density from nearby atoms, thereby diminishing the shielding of the protons by circulating electrons. The hydrogen atoms near electronegative groups are said to be deshielded from the external magnetic field and have a higher resonance frequency than shielded protons. As the EN of the substituent increase, so does the extent of the deshielding effect (and so the chemical shift, see section 6.6.2 for further discussion about the chemical shift) as shown in the examples below.
