5.4 Optical Activity

The two enantiomers are mirror images of each other. They are very alike and share many properties in common, such as the same b.p., m.p., density, color, and solubility. In fact, the pair of enantiomers have the same physical properties, except the way they interact with plane-polarized light.

In normal light, the electric field oscillates in all directions. When normal light passes through a polarizing filter, only light oscillating in one single plane can go through, and the resulting light that oscillates in one single direction is called plane-polarized light.

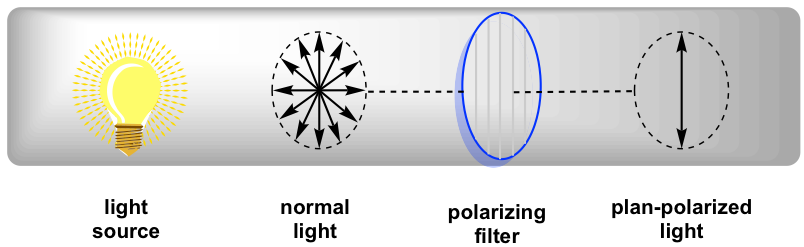
When plane-polarized light interacts with chiral molecules, the plane of polarization will be rotated by the chiral substances. It was first discovered by Jean-Baptiste Biot in 1815 that some naturally occurring organic substances, like camphor, are able to rotate the plane of polarization of plane-polarized light. He also noted that some compounds rotated the plane clockwise and others counterclockwise. Further studies indicate that the rotation is caused by the chirality of the substances.

The property of a compound being able to rotate the plane of polarization of plane-polarized light is called optical activity, and a compound with such activity is labeled as optical active. A stereoisomer that is optical active is also called an optical isomer.

The sample containing a chiral compound rotates the plane of polarization of plane-polarized light, and the direction and angles of the rotation depend on the nature and concentration of the chiral substances. The rotation angles can be measured using a polarimeter (later in this section).

For a pair of enantiomers with the same concentration, under the same conditions, they rotate the plane of polarization with the same angles but in the opposite direction. One is clockwise, and the other is counterclockwise.

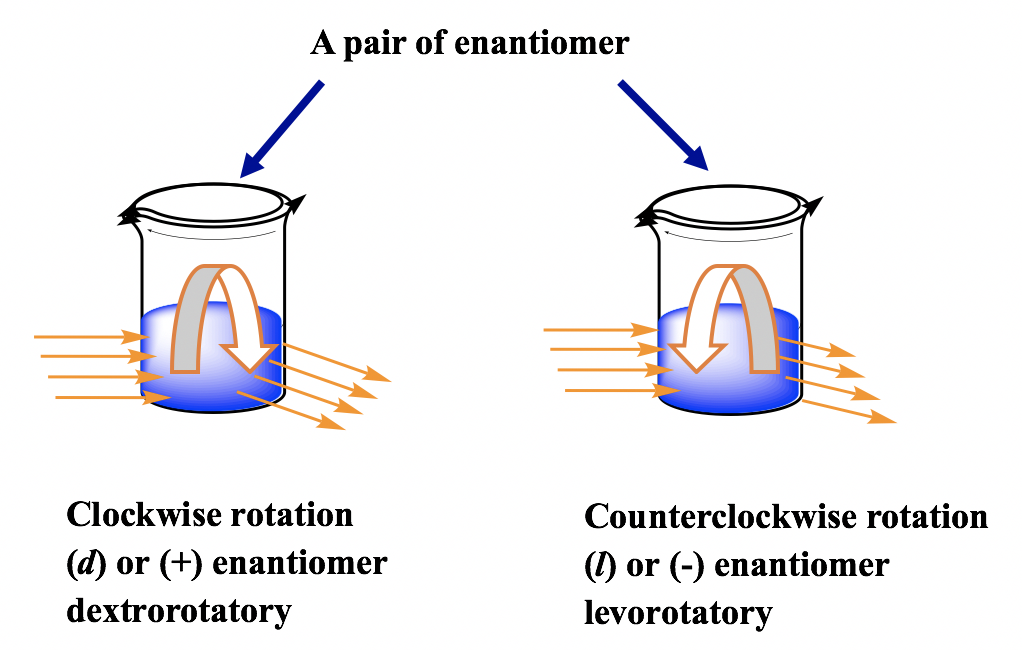
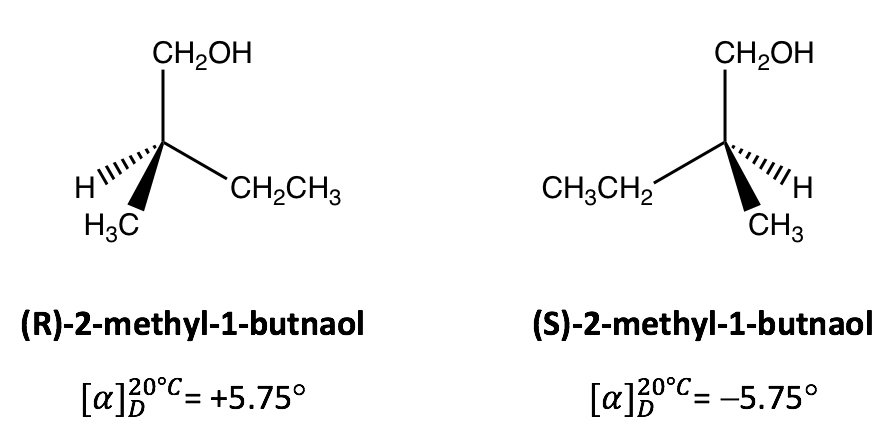
The enantiomer rotates the plane of polarization clockwise and is said to be dextrorotatory (Latin, which means to the right), and it is labeled with the prefix (d) or (+). The enantiomer rotates the plane of polarization counterclockwise and is said to be levorotatory (Latin, which means to the left), and it is labeled with the prefix  (l) or (–). The d/l (or +/-) indicates the direction in which an optical active compound rotates the plane of polarization of plane-polarized light, which has to be determined by an experiment to measure the optical rotation. The d/l (or +/–) symbol has nothing to do with R/S. R/S indicates the arrangement of the groups around the chirality center, which can be determined by knowing the exact spatial arrangement of the groups. That means a compound with an R configuration can be either d or l, and a compound with an S configuration can also be either d or l. For the examples below, both compounds are S-isomers, but one is d (+) and the other is l (-).

The only thing we can be sure of is that for a pair of enantiomers, if one enantiomer has been determined as d, then the other enantiomer must be l, and vice versa.

The polarimeter is an instrument that measures the direction and angles of rotation of plane-polarized light. The plane-polarized light passes through the sample tube containing the solution of a sample, and the angle of rotations will be received and recorded by the analyzer, as summarized in Fig. 5.4c.

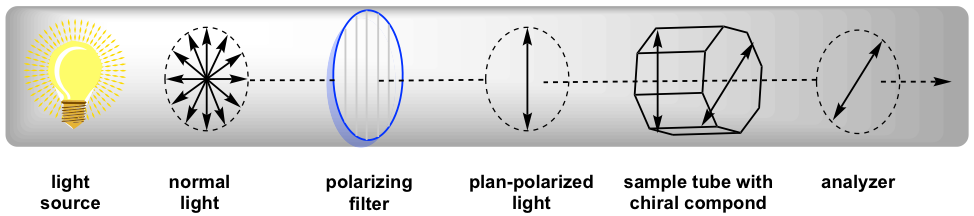
Since the measurement results vary with the wavelength of the light being used, the specific light from a sodium atomic spectrum with the wavelength of 589 nm, which is called the sodium D-line, is used for most polarimeters. The rotation degree measured by the polarimeter is called the observed rotation (α), and the observed rotation depends on the length of the sample tube, the concentration of the sample and the temperature.

To compare the optical rotation between different compounds under consistent conditions, the specific rotation is used. Specific rotation is the rotation caused by a solution with a concentration of 1.0 g/mL in a sample tube of 1.0 dm length. The temperature is usually at 20°C. Based on this definition, the specific rotation can be calculated from the observed rotation by applying the formula:

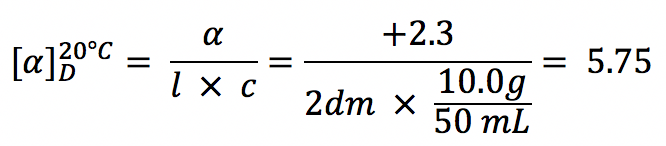
Optical Activity of Different Samples

When a sample under measurement only contains one enantiomer, this sample is called enantiomerically pure, which means only one enantiomer is present in the sample.

The sample may also consist of a mixture of a pair of enantiomers. For such a mixture sample, the observed rotation value of the mixture, together with the information on the specific rotation of one of the enantiomers allows us to calculate the percentage (%) of each enantiomer in the mixture. To do such a calculation, the concept of enantiomer excess (ee) will be needed. The enantiomeric excess (ee) tells how much of an excess of one enantiomer is in the mixture, and it can be calculated as:

 

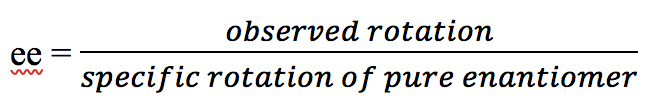
We will use a series of hypothetical examples in the next table for a detailed explanation.

 

If the specific rotation of a (+)-enantiomer is +100°, then the observed rotation of the following samples are (assume the sample tube has a length of 1 dm, and the concentration for each sample is 1.0 g/mL):
Sample Number	Sample	Observed rotation (º)
1	pure (+) enantiomer	+100
2	Pure (-)-enantiomer	-100
3	Racemic mixture of 50% (+)-enantiomer and 50% (-)-enantiomer	0
4	A mixture of 75% (+)-enantiomer and 25% (-)-enantiomer	+50
4	A Mixture of 20% (+)-enantiomer and 80% (-)-enantiomer	-60

 

Sample #1 and #2 are straightforward.

 

Sample #3 is for a mixture with an equal amount of two enantiomers, and such a mixture is called a racemic mixture or racemate. Racemic mixtures do not rotate the plane of polarization of plane-polarized light, which means racemic mixtures are optical inactive and have an observed rotation of zero! This is because for every molecule in the mixture that rotates the plane of polarization in one direction, there is an enantiomer molecule that rotates the plane of polarization in the opposite direction with the same angle, and the rotation gets canceled out. As a net result, no rotation is observed for the overall racemic mixture. The symbol (±) sometimes is used to indicate that a mixture is racemic.

 

In Sample #4, the (+)-enantiomer is in excess. Since there are 75% (+)-enantiomer and 25%(-)-enantiomer, the enantiomeric excess (ee) value of (+)-enantiomer is 75% – 25% = 50%; this can also be calculated by the formula: ee =

In this sample of the mixture, the rotation of the (-)-enantiomer is canceled by the rotation caused by part of the (+)-enantiomer, so the overall net observed rotation depends on how much “net amount” of (+)-enantiomer is present. This can be shown in the diagram below.

 

 

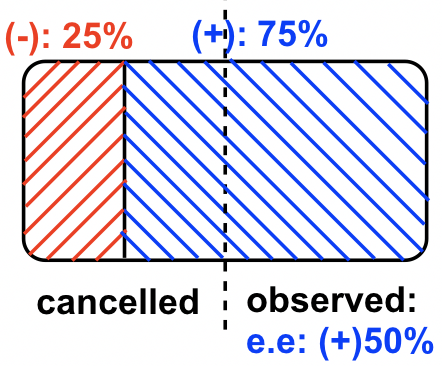
In Sample #5, the (-)-enantiomer is in excess, and because there is 80% (-)-enantiomer and 20% (+)-enantiomer, the enantiomeric excess (ee) value of the (-)-enantiomer is 80% – 20% = 60%; this can also be calculated by the formula: ee =

 

Please note: To calculate the e.e value, it is not necessary to include the sign of the rotation angle, as long as keep in mind that the sign (+ or –) of the observed rotation indicates which enantiomer is in excess.

Exercises 5.6

Draw the diagram for Sample #5 by referring to the diagram for Sample #4.

Answers to Practice Questions Chapter 5

Examples: An advanced level of calculation.

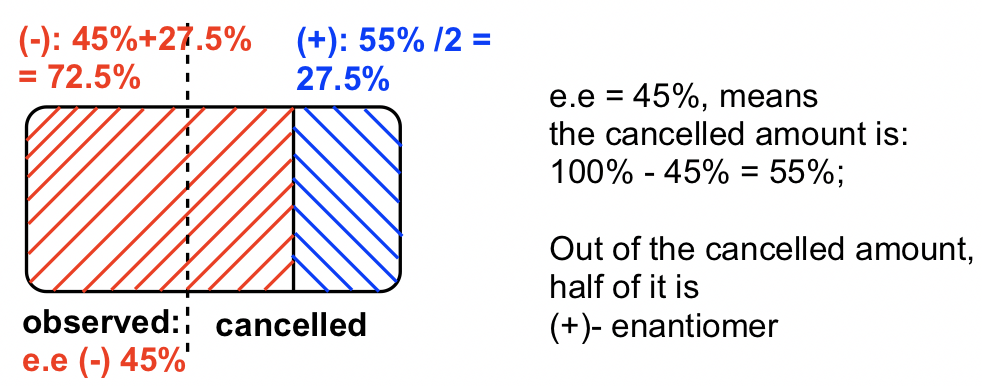
The (+)-enantiomer of a compound has a specific rotation ([α]²⁰_D) of +100°. For a sample (1 g/ml in 1dm cell) that is a mixture of (+) and (-) enantiomers, the observed rotation α is -45°, what is the percentage of (+) enantiomer present in this sample?

Solution:

The observed rotation is in “-”, so the (-)-enantiomer is in excess.

ee of (-)-enantiomer is:

From here, we will see two ways of solving such type of question:

Method I: solving algebra

% of (-)-enantiomer is set as “x”;       % of (+)-enantiomer is set as “y”

x + y = 100%

x – y = 45%

Solve x = 72.5%; y = 27.5%;

So there is 72.5% (-)-enantiomer and 27.5% of (+)-enantiomer in the sample.

Method II: using the diagram, the answer is in blue color, there is 27.5% of (+)-enantiomer.

Chirality and Biological Properties

Other than the optical activity difference, the different enantiomers of a chiral molecule usually show different properties when interacting with other chiral substances. This can be understood by using the analogue example of fitting a hand into its respective glove: the right hand only fits into the right glove, and it feels weird and uncomfortable if you wear a left glove on the right hand. This is because both the right hand and right glove are chiral. A chiral object only fits into a specific chiral environment.

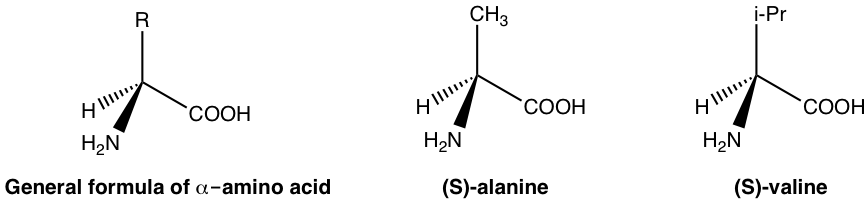
In the human body, biological functions are modulated by enzymes and receptors. Enzymes and receptors are essentially proteins, and proteins are made up of amino acids. Amino acids are examples of naturally occurring chiral substances. With the general formula given below, the carbon with an amino (NH₂) group is the chirality (asymmetric) center for most amino acids, and only one enantiomer (usually an S-enantiomer) exists in nature. A few examples of amino acids are given below with the general formula.

 

Because amino acids are chiral, proteins are chiral, so enzymes and receptors are chiral as well. The enzymes or receptors therefore form the chiral environment in the human body that distinguishes between R or S enantiomers. Such selectivity can be illustrated by the simple diagram below.

 

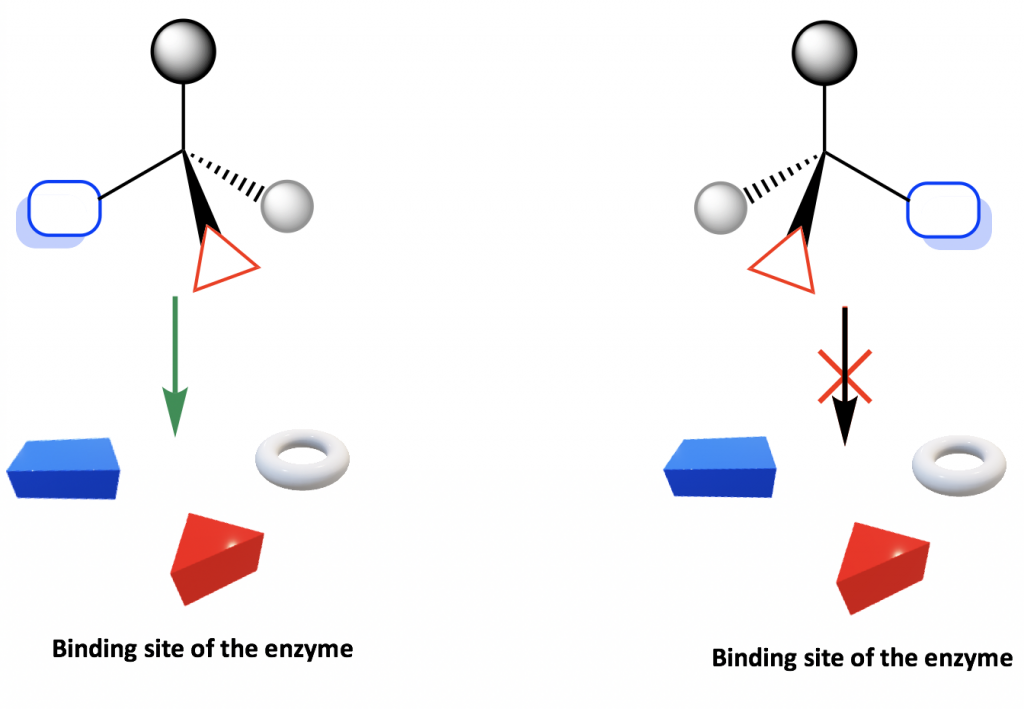
The binding site of an enzyme or receptor is chiral, so it only binds with the enantiomer whose groups are in proper positions to fit into the binding site. As shown in the diagram, only one enantiomer binds with the site, but not the other enantiomer.

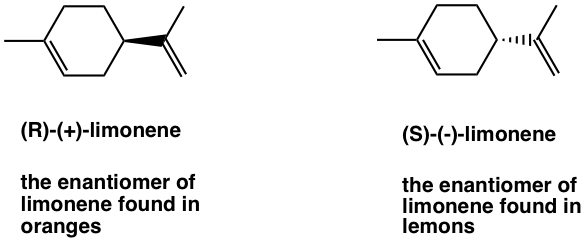
A couple of common examples to showcase such binding selectivity of different enantiomers may include limonene and carvone.

Limonene has two enantiomers, and they smell completely different to human beings because they interact with different receptors located in the nerve cells in the nose. The (R)-(+)-limonene is responsible for the smell of oranges, and the (S)-(-)-limonene gives the smell of lemon.

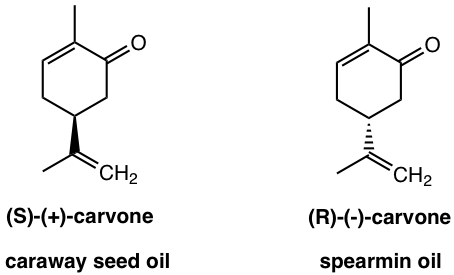
If you like caraway bread, this smell is due to the (S)-(+)-carvone, and the (R)-(-)-carvone that is found in spearmint oil gives it a much different odor.

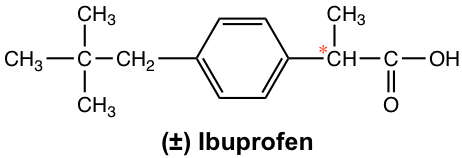
More dramatic examples of how chirality plays an important role in biological properties are found in many medicines. For the common over-the-counter anti-inflammatory drug ibuprofen (Advil), for example, only the (S)-enantiomer is the active agent, while the (R)-enantiomer has no anti-inflammatory effects. Fortunately, the (R)-enantiomer does not have any harmful side effects and slowly converts to the (S)-enantiomer in the body. Ibuprofen is usually marketed as a racemate form.

The issue of chiral drugs (drugs that contain a single enantiomer, not as a racemate) did not gain the attention of the drug discovery industry until 1960. Back then, drugs were approved in racemate form if a chirality center was involved, and there was no further study on the biological differences of different enantiomers. These were all changed by the tragic case of thalidomide. Thalidomide was a drug sold in more than 40 countries, mainly in Europe, in the early 1960s as a sleeping aid and to pregnant women as an antiemetic (a drug that prevents vomiting) to combat morning sickness. It was not recognized at that time that only the R-enantiomer has the antiemetic property, while the S-enantiomer was a teratogen that causes congenital deformations. The drug was marketed as a racemic mixture and caused damage in about 10,000 children before it was withdrawn from the market in Nov. 1961. This drug was not approved in the US, but it was attributed to Dr. Frances O. Kelsey, who was a physician for the Food and Drug Administration at that time and had insisted on additional tests on some side effects. Thousands of lives were saved by Dr. Kelsey, and she was awarded the President’s Medal in 1962 for preventing the sale of thalidomide.