4.3 Conformation Analysis of Cyclohexane

Chair conformation of cyclohexane

Cyclohexane is the most stable cycloalkane. It is strain-free, meaning neither angle strains nor torsional strains apply, and it shows the same stability as chain alkanes. This special stability is due to a unique conformation it adopts. The most stable conformation of cyclohexane is called the “chair“ conformation, since it somewhat resembles a chair.

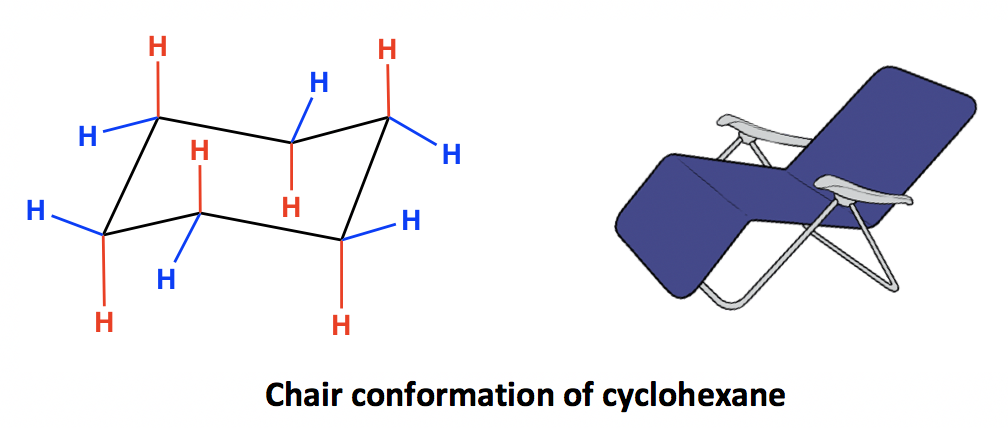
In the chair conformation of cyclohexane, all the carbons are at 109.5º bond angles, so no angle strain applies. The hydrogens on adjacent carbons are also arranged in a perfectly staggered conformation that makes the ring free of torsional strain as well. This will be illustrated more clearly later when we learn about the Newman projection of the chair conformation.

Properties of the chair conformation

In the chair conformation of cyclohexane, the twelve C-H bonds can be divided into two categories based on the orientations, which are axial (“a”) and equatorial (“e”). In the structure below, the six red-coloured bonds are axial, and the six blue-coloured bonds are equatorial. Axial bonds are vertical and perpendicular to the average plane of the ring, while the equatorial bonds are more “flat” and extend from the perimeter of the ring. For both “a” and “e”, they can either point up ↑(above the ring), or point down ↓(below the ring). The trending of “a” and “e” bonds in the chair conformation can be summarized as:

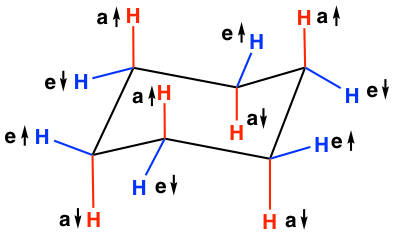
• Each carbon has one “a” bond and one “e” bond; if one bond points up ↑(above the ring), the other has to point down ↓(below the ring)
• For the same type of bonds, the orientation up ↑ and down ↓ alternates from one carbon to the adjacent carbon, meaning if a certain carbon has a ↑, then the adjacent carbon must have a ↓
• For the twelve C-H bonds: 3a↑ , 3 a↓, 3 e↑ , and 3 e↓.

How to draw the chair conformation

It is important to understand and recognize all the bonds in the chair conformation, and you are also expected to be able to draw the conformation correctly and quickly. The procedure is:

1. Draw two parallel lines of the same length that both point slightly down (if connected, they would form a parallelogram with an internal angle of about 60°/120°).
2. Connect the right ending points of the two lines with a “V” shape so that the vertex of the V points to the upper right
3. Connect the left starting points of the two lines with another “V” shape so that the vertex of the V points to the bottom left
4. Add up all of the “a” bonds on each carbon as the vertical lines, and follow the alternating trend on adjacent carbons
   
5. Add all of the “e” bonds by following the trend in which on a certain carbon, if an “a” bond points up, then an “e” bond must point down, and vice versa. Also notice that the “e” bond is parallel to the C-C bond which is one bond away, as shown below. The “green e” is parallel to the “green C-C bond”, and the “blue e” is parallel to the “blue C-C bond”. (It is more challenging to draw “e” bonds, and following the above trend makes it easier).

Ring flipping

When a cyclohexane ring undergoes a chair-chair conformation conversion, this is known as ring flipping. Ring flipping comes from C-C bond rotation, but since all of the bonds are limited within the ring, the rotation can only partially occur, which leads to the ring “flipping”. Cyclohexane rapidly interconverts between two stable chair conformations because of the ease of bond rotation. The energy barrier is about 45 kJ/mol, and the thermal energies of the molecules at room temperature are high enough to cause about 1 million interconversions to occur per second.

For cyclohexane, the ring after flipping still appears almost identical to the original ring, but some changes happen on the C-H bonds. Specifically, all the “a” bonds become “e” bonds, and all the “e” bonds become “a” bonds; however, their relative positions in terms of the ring, up or down, remain the same. The ring flipping is shown in the equation below. Compare the carbon with the same numbering in the two structures to see what happened to the bonds due to ring flipping.

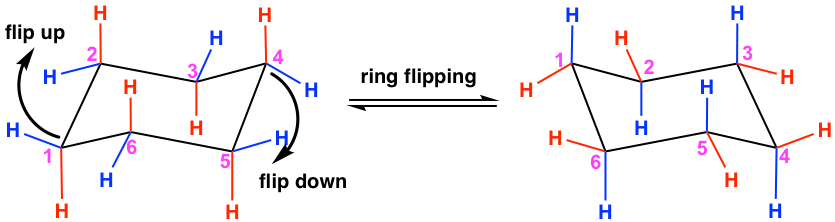
Taking C #1 as an example, you will notice that the red a↓ converted to a red e↓,  and the blue e↑ converted to a blue a↑ after ring flipping.

Newman projection of the chair conformation

The chair conformation is strain-free, with all the C-H bonds in a staggered position. However, it is not easy to see the staggered conformation in the drawings we have so far, and a Newman projection helps for this purpose.

To draw Newman projections for the chair conformation of cyclohexane, we also need to pick up the C-C bonds to view along, just as we did for alkanes. Since there are a total of six C-C bonds, we will pick two of them, and these two need to be parallel to each other.

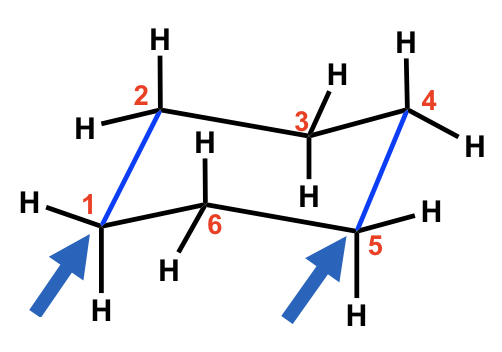
For the chair conformation example here, the two blue parallel C-C bonds, C1-C2 and C5-C4, are chosen for viewing. (There are 3 pairs of parallel bonds in the chair conformation, and any pair can be chosen with the resulting Newman projection looking the same).

For the C1-C2 bond, C1 is the ‘front” carbon and C2 is the “rear” carbon. For the C5-C4 bond, C5 is the ‘front” carbon and C4 is the “rear” carbon. These two bonds will be represented by two “Newman projections” we are familiar with (two circle things), and each represents two carbons, as shown below:

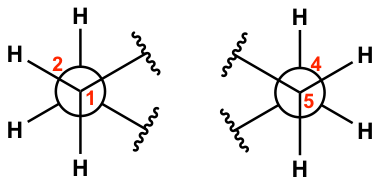
Keep in mind that there are a total of six carbons in the ring, and the drawing above only shows four of them with C3 and C6 being left out. Additionally, the two “separated” Newman projections above are actually connected to both C3 and C6, so the overall Newman projection of the chair conformation of cyclohexane looks like this:

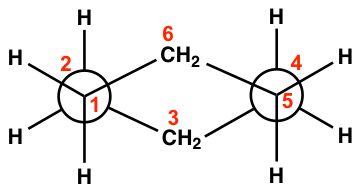
The staggered conformation of hydrogens is clearly shown in the Newman projection here!

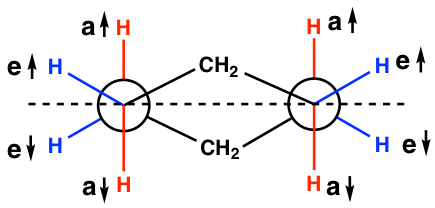
Notes for Newman projections of the chair conformation (refer to the drawing below):

• The “a” or “e” bonds on four carbons (C1, C2, C4 and C5) are shown explicitly, while the bonds on C3 and C6 are just shown as CH₂.
• The vertical red C-H bonds are the “a” bonds, and the “flat” blue C-H bonds are the “e” bonds.
• The dashed line in the drawing below can be regarded as the average plane of the ring. Those above the line are the bonds that point up ↑, and those below the line are the bonds that point down ↓.

Other conformation of cyclohexane

The chair conformation is the most stable one with the lowest energy, but it is not the only conformation for cyclohexane. During the ring flipping from one chair conformation to another, the ring goes through several other conformations, and we will only briefly discuss the boat conformation here.

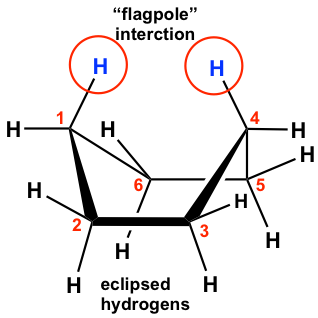
The boat conformation comes from partial C-C bond rotations (only flipping one carbon up to convert the chair to a boat) of the chair conformation, and all the carbons still have 109.5º bond angles, so there are no angle strains. However, the hydrogens on the base of the boat are all in eclipsed positions, so there are torsional strains. This can be illustrated by the Newman projection below. The Newman projection is drawn by viewing along C6-C5 and C2-C3 bonds of the above boat conformation.

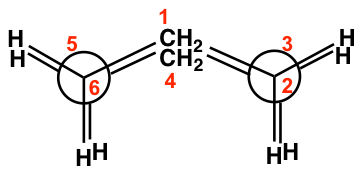
Other than that, the two hydrogen atoms on C1 and C4 are very close to each other and cause steric strain. This is also called the “flagpole” interaction of the boat conformation. The two types of strains make the boat conformation have considerably higher energy (about 30 kJ/mol) than the chair conformation.