Chapter 9: Conservation of Momentum

Equations Introduced and Used in this Topic (all equations can be written and solved as both scalar and vector and all equations are generally solved as vectors):
In an Isolated System
[latex]\Sigma\overrightarrow{p} = constant[/latex]
or … [latex]\underrightarrow{p}_{before} =\underrightarrow{p}_{after} (Vector Equation)[/latex]
[latex]Where ...\underrightarrow{p} =m\underrightarrow{v}[/latex]
For two or more bodies:
p1i (x, y, z) + p2i (x, y, z) + … = p1f (x, y, z) + p2f (x, y, z) + …
Where
[latex]\overrightarrow{p}[/latex] Momentum is the product of Mass times Velocity and is measured in either Newton-Seconds (Ns) or Kilograms Metres per Second (kg m/s)
m is Mass, commonly measured in Kilograms (Kg), Grams (g) or Tonnes (t)
[latex]\overrightarrow{v}[/latex] is the Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
CANNOT FIND THIS IMAGE OR ANYTHING LIKE IT– lolscience webpage not in existance
Image is of the electron-positron (antimatter) particles being created in the lab. (Image source: lolscience.co.uk)
The Law of the Conservation of Momentum 3 is one of the most powerful and useful laws in the study of mechanics. It belongs to a family of four conservation laws: Conservation of Mass Energy, Conservation of Electric Charge, Conservation of Linear Momentum and Conservation of Angular Momentum 4.
The law of conservation of momentum is derived mainly from Newton’s Third Law and can be analyzed as in the following description excerpted from the Physics Classroom:
In every interaction, there is a pair of forces acting on the two interacting objects. The size of the force on the first object equals the size of the force on the second object. The direction of the force on the first object is opposite to the direction of the force on the second object. Forces always come in pairs – equal and opposite action-reaction force pairs.
9.1 Total Momentum: the resolution of multiple momentum vectors
Total Momentum of a System: The Resolutions of multiple momentums acting during an event or interaction
Momentums are Vectors. They are added, subtracted and combined according to the direction they take. Quite often, vectors in different directions, such as North and South, East and West, and up and down, are left as the sum of the three different vector directions and not combined any further.
Vectors in the same directions are added and vectors in the opposite direction are subtracted.
For instance:
100 Ns East + 50 Ns East = 150 Ns East
(The vectors are in the same direction so they are added.)
100 Ns North + 50 Ns South = 50 Ns North
(The vectors are in the opposite direction so they are subtracted.)
Vectors in different directions are generally left as the vector sum in each of those directions.
For instance:
100 Ns North + 50 Ns East = 100 Ns North + 50 Ns East
(The vectors are in the different direction so they are left alone.)
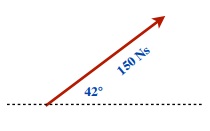
Vectors that are angled between two directions are first broken up into the various components for those directions before they are added or subtracted.
For instance: Using right angle trigonometry, this 150 Ns vector would be broken up into the force directed upwards and the force to the left.
To find the Momentum upwards use the Sine function:
Sin 42° = Momentum up
150 Ns
To find the Momentum right use the Cosine function:
Cos 42° = Momentum right
150 Ns
EXAMPLE 9.1.1
Resolve the following multiple momentum vectors:
a. 
b. 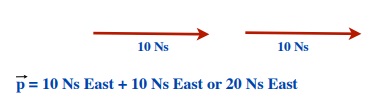
c. 
d. 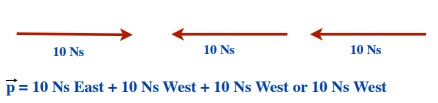
e. 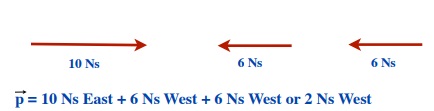
f.
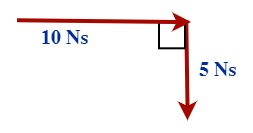
[latex]\overrightarrow{p}[/latex] = 10 Ns East + 5.0 Ns South (left like this)
g. 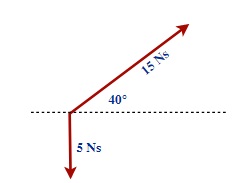
Breaking up the 15 Ns, we get:
[latex]\overrightarrow{p}_{north}[/latex] = 15s Sin 40º or 9.6 Ns North
[latex]\overrightarrow{p}_{east}[/latex]= 15 Ns Cos 40º or 11.5 Ns East
[latex]\overrightarrow{p}[/latex] = 11.5 Ns East + 9.6 Ns North + 5.0 Ns South…
Result is 11.5 NsEast + 4.6 Ns North
(≈ 12 Ns East + 4.6 Ns North)
h. 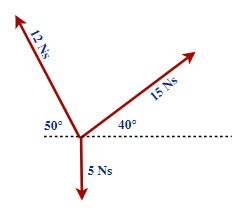
Breaking the 15 Ns, we get:
[latex]\overrightarrow{p}_{north}[/latex]= 15s Sin 40º or 9.6 Ns North
[latex]\overrightarrow{p}_{east}[/latex]= 15 Ns Cos 40º or 11.5 Ns East
Breaking up the 12 Ns, we get:
[latex]{p}_{north}[/latex]= 12s Sin 50º o r9.2 Ns North
[latex]{p}_{east}[/latex]= 12 Ns Cos 50º or 7.7 Ns West
[latex]\overrightarrow{p}[/latex] = 9.6 Ns North + 9.2 Ns North + 5 Ns South or 13.8 Ns North
[latex]\overrightarrow{p}[/latex] = 11.5 Ns East + 7.7 Ns West or 3.8 Ns East
Resultant is [latex]\overrightarrow{p}[/latex] = 13.8 Ns North + 3.8 Ns East
(≈ 14 Ns North + 3.8 Ns East)
9.2 Linear Collisions 5, 6, 7

In an Isolated System
[latex]\Sigma\overrightarrow{p}[/latex] = constant
or …
[latex]\underrightarrow{p}_{before} =\underrightarrow{p}_{after}[/latex](Vector Equation)
Where [latex]\underrightarrow{p} = m\underrightarrow{v}[/latex]
For two or more bodies:
[latex]\underrightarrow{p}_{li(x, y, z)} +\underrightarrow{p}_{2i(x, y, z)} + ... =\underrightarrow{p}_{1f(x, y, z)} +\underrightarrow{p}_{2f(x, y,z)} + ...[/latex]
The Law of Momentum Conservation is one of the foundational laws in Physics. The law is stated as follows:
In the absence of external forces that can change the momentum of objects inside a system from the outside, the vector sum of the momentum of all objects moving within the system will equal the vector sum of momentum of these same objects after an interaction has occurred, be it a collision or explosion.
This absence of external forces acting on the object means that the system being looked at is termed an isolated system8. Isolated systems require that no external forces outside of the forces acting between the objects within a system can be acting. This means that the forces acting on the objects are in fact being balanced between the objects and not by outside means.
[latex]\overrightarrow{F}orce_{object1} = -\overrightarrow{F}orce_{object2}[/latex]
These forces are equal in strength (magnitude) but act in opposite directions.
These forces can only act on each other for exactly the same amount of time, meaning:
[latex]time_{object1} = time_{object2}[/latex]
You should recognize that we are talking about equal and opposite Impulses (Chapter 7) that are acting on the two colliding bodies. This means that:
[latex](\overrightarrow{F}orce_{object1})(time_{object1})= -(\overrightarrow{F}orce_{object2})(time_{object2})[/latex]
You can conclude from this that we are talking about equal and opposite changes in momentum (Chapter 7) that will result from the equal and opposite impulses that are acting on the two colliding bodies. This means that:
[latex](mass_{object1})(\Delta\overrightarrow{v}elocity_{object1}) = -(mass_{object2})(\Delta\overrightarrow{v}elocity_{object2})[/latex]
The changes in momentum that occur for either body are both equal and opposite.
If two objects collide, the forces acting between the two objects are equal and opposite as defined by Newton’s Third Law.
EXAMPLE 9.2.1
A circus cannon on wheels (500 kg) launches a clown of mass 65 kg with a horizontal velocity of 4.2 m/s; calculate:
Data:
(i) Momentum of the clown (before and after)
(ii) The combined momentum of the clown and circus cannon before and after firing
(iii) The speed at which this circus cannon recoils if originally at rest
| [latex]\text{m cannon = 500 kg}[/latex] | [latex](i)\overrightarrow{p}_{iclown}=\text{(65 kg)(0 m/s) or 0 Ns}[/latex] |
| [latex]\overrightarrow{v}_{icannon} =\text{0 m/s}[/latex] | [latex]\overrightarrow{p}_{fclown}=\text{(65 kg)(4.2 m/s) or 273 Ns (≈ 270 Ns)}[/latex] |
| [latex]\overrightarrow{v}_{fcannon} = unknown[/latex] | |
| [latex]\text{m clown = 65 kg}[/latex] | [latex](ii)\overrightarrow{p}_{iclown} +\overrightarrow{p}_{icannon} =\text{0 Ns}[/latex] |
| [latex]\overrightarrow{v}_{fclown} =\text{0 m/s}[/latex] | [latex]Therefore...\overrightarrow{p}_{fclown} +\overrightarrow{p}_{fcannon} =\text{0 Ns}[/latex] |
| [latex]\overrightarrow{v}_{fclown} = 4.2 m/s[/latex] |
[latex](iii)\overrightarrow{p}_{iclown} +\overrightarrow{p}_{icannon} =\overrightarrow{p}_{fclown} +\overrightarrow{p}_{fcannon}[/latex]
[latex](m_{clown})(\overrightarrow{v}_{iclown})+(m_{cannon})(\overrightarrow{v}_{icannon})=(m_{clown})(\overrightarrow{v}_{fclown})+(m_{cannon})(\overrightarrow{v}_{fcannon})[/latex]
(65 kg)(0 m/s) + (500 kg)(0 m/s) = (65 kg)(4.2 m/s) + (500 kg)[latex](\overrightarrow{v}_{fcannon})[/latex]
0 Ns + 0 Ns = 273 Ns + (500 kg)[latex](\overrightarrow{v}_{fcannon})[/latex]
[latex](\overrightarrow{v}_{fcannon})[/latex]= -273 Ns ÷ 500kg or – 0.55 m/s (cannon recoils backwards)
EXAMPLE 9.2.2
A 4.0 kg curling rock moving 0.5 m/s West collides with a stationary 4.0 kg curling rock at rest. If the original curling rock comes to a full stop upon collision, at what velocity should the second curling rock be moving?
Data:
| [latex]\overrightarrow{p}_{irock1}+\overrightarrow{p}_{irock2}=\overrightarrow{p}_{frock1}+\overrightarrow{p}_{frock2}[/latex] | |
| [latex]m_{rock1}=\text{4.0 kg}[/latex] | |
| [latex]\overrightarrow{v}_{irock1}=\text{0.5 m/s}[/latex] | [latex](m_{rock1})(\overrightarrow{v}_{rock1})+(m_{rock2})(\overrightarrow{v}_{irock2})=(m_{rock1})(\overrightarrow{v}_{frock1})=(m_{rock2})(\overrightarrow{v}_{frock2})\text{West}[/latex] |
| [latex]\overrightarrow{v}_{frock1}=\text{0 m/s}[/latex] | [latex]\text{(4.0 kg)(0.5 m/s West) + (4.0 kg)(0 m/s) = (4.0 kg)(0 m/s) + (4.0 kg}(\overrightarrow{v}_{frock2})[/latex] |
| [latex]\text{2.0 Ns West + 0 Ns = 0 Ns + (4.0 kg)}(\overrightarrow{v}_{frock2})[/latex] | |
| [latex]\overrightarrow{v}_{irock2}=\text{0 m/s}[/latex] | |
| [latex]\overrightarrow{v}_{frock2}=\text{find}[/latex] | [latex](\overrightarrow{v}_{frock2})=\text{ 2.0 Ns West ÷ 4.0 kg or 0.5 m/s West}[/latex] |
[latex]\overrightarrow{p}_{irock1}+\overrightarrow{p}_{irock2}=\overrightarrow{p}_{frock1}+\overrightarrow{p}_{frock2}[/latex]
[latex]m_{rock1}= 4.0 kg[/latex]
[latex]\overrightarrow{v}_{irock1}= 0.5 m/s (m_{rock1})(\overrightarrow{v}_{rock1})+(m_{rock2})(\overrightarrow{v}_{irock2})=(m_{rock1})(\overrightarrow{v}_{frock1})=(m_{rock2})(\overrightarrow{v}_{frock2})West[/latex]
[latex]\overrightarrow{v}_{frock1}[/latex]= 0 m/s (4.0 kg)(0.5 m/s West) + (4.0 kg)(0 m/s) = (4.0 kg)(0 m/s) + (4.0 kg)[latex](\overrightarrow{v}_{frock2})[/latex]
m = 4.0 kg 2.0 Ns West + 0 Ns = 0 Ns + (4.0 kg)[latex](\overrightarrow{v}_{frock2})[/latex]
[latex]\overrightarrow{v}_{irock2}[/latex] = 0 m/s
[latex]\overrightarrow{v}_{frock2}= find[/latex] [latex](\overrightarrow{v}_{frock2})[/latex]= 2.0 Ns West ÷ 4.0 kg or 0.5 m/s West
EXAMPLE 9.2.3
During a tackle in a football game, two players of mass 90 kg and 70 kg were moving towards each other, and after collision both came to a full stop. If the velocity of the larger player before collision was 7.0 m/s what was the velocity of the smaller player?
Directions: all we have for the direction in this problem is that both players were running towards each other.
Data:
m90 = 90 kg [latex]\overrightarrow{p}_{i90}+\overrightarrow{p}_{i70}=\overrightarrow{p}_{f90}+\overrightarrow{p}_{f70}[/latex]
[latex]\overrightarrow{v}_{i90}= 7.0 m/s[/latex] [latex](m_{90})(\overrightarrow{v}_{i90})+(m_{70})(\overrightarrow{v}_{i70})-(m_90)(\overrightarrow{v}_{f90})+(m_70)(\overrightarrow{v}_{f70})[/latex]
[latex]\overrightarrow{v}_{f90}= 0 m/s[/latex]
(90 kg)(7.0 m/s) + (70 kg)[latex](\overrightarrow{v}_{i70})[/latex] = (90 kg)(0 m/s) + (70 kg)(0 m/s)
m 70 = 70 kg 630 Ns + (70 kg)[latex](\overrightarrow{v}_{i70})[/latex] = ) Ns + 0 Ns
[latex]\overrightarrow{v}_{i70}[/latex] = find
[latex]\overrightarrow{v}_{f70} = 0 m/s (\overrightarrow{v}_{i70})[/latex] = – 630 Ns ÷ 70 kg or – 9.0 m/s
Note: The – 9.0 m/s means that the smaller player was running in the opposite direction from (towards) the larger player.
EXAMPLE 9.2.4
If a 16 kg medicine ball is thrown horizontally to a stationary 65 kg skater on ice (consider this to be frictionless) and causes the skater who is now holding the ball to move off with a horizontal velocity of 0.50 m/s, at what velocity was the ball thrown?
Data:
| [latex]\overrightarrow{p}_{i16}+\overrightarrow{p}_{i65}=\overrightarrow{p}_{f16}+\overrightarrow{p}_{f65}[/latex] | |
| [latex]m_{16} =\text{16 kg}[/latex] | |
| [latex]\overrightarrow{v}_{i16}= find[/latex] | [latex](m_{16})(\overrightarrow{v}_{i16})=(m_{65})(\overrightarrow{v}_{i65})=(m_{16})(\overrightarrow{v}_{f16})+(m_{65})(\overrightarrow{v}_{f65})[/latex] |
| [latex]v_{f16}=\text{0.50 m/s}[/latex] | |
| [latex](16 kg)(\overrightarrow{v}_{i16)}+\text{(65 kg)(0 m/s) = (16 kg + 65 kg)(0.5 m/s)}[/latex] | |
| [latex]\text{m 65 = 65 kg}[/latex] | [latex](\overrightarrow{v}_{i16}) +\text{(0 Ns) = 40.5 Ns)}[/latex] |
| [latex](\overrightarrow{v}_{i65}) =\text{0 m/s}[/latex] | |
| [latex]\overrightarrow{v}_{f65}=\text{0.50 m/s}[/latex] | [latex]\overrightarrow{v}_{i16} =\text{ 40.5 Ns ÷ 16 kg ≈ 2.5 m/s horizontally}[/latex] |
Note: The ≈ + 2.5 m/s means that both the ball and the skater continue moving in the same horizontal direction that the medicine ball was thrown.
QUESTIONS 9.3 Linear Collisions
1. A cannon on wheels (2750 kg) shoots a cannon ball of mass 14.7 kg. If this cannon ball leaves the muzzle with a horizontal velocity of 487 m/s, calculate:
(i) The momentum of this cannon ball (before and after)
(ii) The combined momentum of the cannon ball and cannon before and after firing
(iii) The recoil velocity of this cannon
2. A 0.40 kg rock moving 0.50 m/s West collides with a stationary 0.50 kg rubber ball at rest. If the 0.40 kg rock comes to a full stop upon collision what velocity should this ball have?
3. During a dynamics experiment two trolley cars of masses 9.0 kg and 6.0 kg were moving towards each other and after collision both came to a full stop. If the velocity of the larger trolley car before collision was 0.025 m/s, what was the velocity of this smaller trolley car?
4. In a bakery fight, a 2.0 kg mass of bread dough moving at 16.0 m/s North collides with a stationary molasses container. The two objects coalesce and move off at 7.50 m/s North. What was the mass of the stationary molasses container?
5. An 800 kg asteroid in space has a velocity of 5.00 m/s. An explosion21 causes the rear section (mass 240 kg) of this asteroid to be sent in the opposite direction at 1.20 m/s. At what velocity did the remaining part of this asteroid continue to move?
6. If a 5.40 g bullet is fired horizontally into a suspended 10.0 kg block of wood and causes the block with bullet embedded to move off with a horizontal velocity of 0.30 m/s, what was the impact velocity of this bullet?
7. Brian’s 10 gram toy train car is traveling at 5.0 cm/s when it collides with a 15 gram tank car originally at rest. If the two cars lock together, at what speed should they travel off?
8. A 95 kg hockey player is skating at 12 m/s when he runs into a larger 120 kg player that is only skating at 5.0 m/s in the same direction. If the two skaters become entangled, at what speed do they slide off?
9. A 105 kg fullback is running straight towards the end zone at 9.5 m/s. A 95 kg defensive back is running straight towards the fullback, tackling the fullback, and both drop to the ground with a velocity of 0 m/s. What was the velocity of this defensive back prior to the tackle?
10. Kyle’s small toy train boxcar of mass of 60 g is rolling at 4.0 cm/s towards a flatcar of mass 45 g that is stationary. If the two cars lock together, at what speed do they continue to move down the track?
11. In the movies, an object such as a football is thrown at a running person, striking and stopping them. If we consider a 70 kg person, running toward you at 8.0 m/s, at what speed must a 2.0 kg football be thrown to stop this person?
12. A medicine ball is thrown at 8.0 m/s towards a stationary 55 kg skater on ice. After she catches it, both the skater and the ball move off at 0.8 m/s. What is the mass of this medicine ball?
13. A large railway wagon, mass 4200 kg, rolls down a track at 2.5 m/s and collides with a smaller wagon, mass 2750 kg, moving at 1.0 m/s in the same direction. If the smaller wagon has a velocity of 3.0 m/s after the collision, what is the final velocity of the large wagon?
14. A small particle A of mass 1.41 x 10-5 g moving at 3.33 x 103 m/s is hit by particle B moving at 5.46 x 104 m/s in the same direction. As a result, particle A increased its velocity to 6.66 x 103 m/s and particle B was slowed to 4.60 x 103 m/s in the original direction. What was the mass of particle B?
15. A 0.85 kg spring toy (at rest) “pops” into 3 pieces. The largest piece of mass 0.45 kg moves at 5.0 cm/s to the right. A smaller piece of mass 0.25 kg moves at 8.0 cm/s to the left. At what speed does the remaining piece move off?
16. A small 65 kg hockey player takes a run at larger 115 kg player at rest. If the smaller player was traveling at 16 m/s towards the larger before the collision and rebounded at 4 m/s after, at what speed did the larger player move off?
9.4 Two Dimensional Collisions 9, 10, 11

In an Isolated System
[latex]\Sigma\overrightarrow{p} = constant[/latex]
or
[latex]\underrightarrow{p}_{before} =\underrightarrow{p}_{after}\text{(Vector Equation)}[/latex]
Where [latex]\underrightarrow{p} = m\underrightarrow{v }[/latex]
For two or more bodies:
[latex]\underrightarrow{p}_{li(x, y, z)} +\underrightarrow{p}_{2i(x, y, z)} +...=\underrightarrow{p}_{2f(x, y, z)}+ ...[/latex]
The Law of the Conservation of Momentum can be expanded from linear one-dimensional to the multi-dimensional universe of 2 or 3 dimensions. This is due to the fact that momentum must be conserved in its original sum as long as no external forces act to change the momentum of the system.
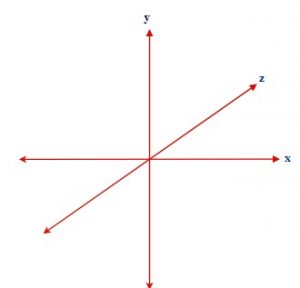
The grid shown to the left is the common (x, y, z) representation of 3 dimensional space. All that is missing from this would be the time that identifies the spot where an object would be at a specific time.
It is also common to see vector momenta sums to be identified according to the directions defined by
(x, y, z).
As such, you could see the momentum of an object defined by:
[latex]\overrightarrow{p}_{iobject} =\overrightarrow{p}_{ix} +\overrightarrow{p}_{iy} +\overrightarrow{p}_{iz}[/latex]
When solving two or three dimensional problems using the Law of Conservation of Momentum, you solve as you did before with the one dimensional problems, except now you need to make sure that the momentum in each of the three directions is conserved both before and after an event occurs.
This means that:
[latex]\overrightarrow{p}_{before(x, y, z)} =\overrightarrow{p}_{after(x, y, z})[/latex]
As an example of this, if the vector sum of the momentum of two or more interacting objects is:
[latex]\overrightarrow{p}_{before(x, y, z)}[/latex]= 25 Ns x – 30 Ns y + 10 Ns z
then the vector sum of the momentum of two or more interacting object afterwards is:
[latex]\overrightarrow{p}_{after(x, y, z)}[/latex]= 25 Ns x – 30 Ns y + 10 Ns z
In solving these two or three dimensional problems, you will be using trigonometry and the Pythagorean Theorem extensively, as you can see in the following two examples.
EXAMPLE 9.3.1
A 120 kg lineman is running at 8.5 m/s North and tackles a 85 kg halfback running at 9.6 m/s East. At what velocity do these two move after the tackle occurs?
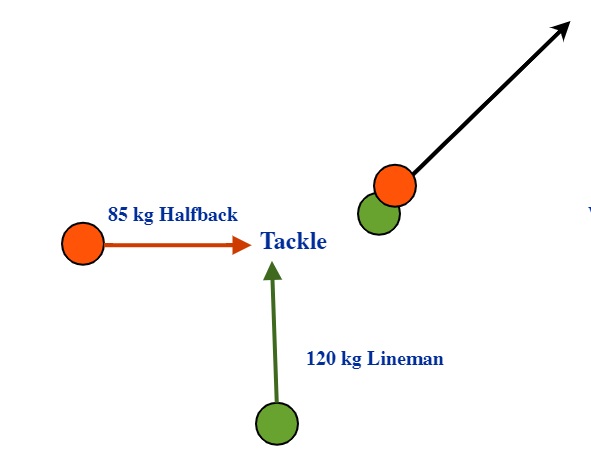
First, find the momenta of the two football players heading into the tackle:
The 8 5kg Halfback: [latex]\overrightarrow{p}_{85} = m_{85}\overrightarrow{v}_{i85}[/latex]
p85 = (85 kg)(9.6 m/s East) or 816 Ns East
The 120 kg Lineman: [latex]\overrightarrow{p}_{120} = m_{120}\overrightarrow{v}_{i120}[/latex]
p120 = (120 kg)(8.5 m/s North) or 1020 Ns North
The total momentum before the tackle is 816 Ns East + 1020 Ns North
Now, in the absence of any other forces acting during this collision, the total momentum after the tackle for these two players must also be 816 Ns East + 1020 Ns North.
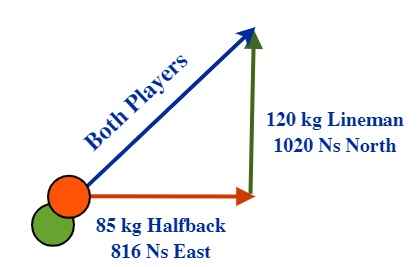
At this point, you will use trigonometry and the Pythagorean Theorem to further analyze this collision.
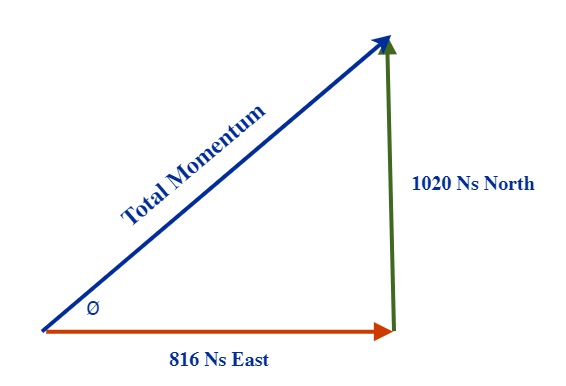
Now: The total momentum can be found by using the Pythagorean Theorem.
[latex](\overrightarrow{p}_{total})^{2} = (816 Ns)^{2} + (1020 Ns)^{2}[/latex]
[latex](\overrightarrow{p}-{total})^{2} = 665856 N^{2}s^{2} + 1040400 N^{2}s^{2}[/latex]
[latex](\overrightarrow{p}_{total})^{2} = 1706256 N^{2}s^{2}[/latex]
[latex]\overrightarrow{p} total = 1306 Ns[/latex]
The angle at which these players move off is now found by using trigonometry, specifically the Tangent function:
Tan ø = Opposite Side / Adjacent Side
Tan ø = 1020 Ns / 819 Ns
Tan ø = 1.245
ø = Tan-1 1.245
ø = 51.3° specifically ≈ 51° North from East
The velocity at which these players move off can be found by using the equation for momentum:
[latex]\overrightarrow{p} = m\overrightarrow{v}[/latex]
[latex]\text{1306 NS = (120 kg + 85 kg)}\overrightarrow{v}_{f(120+85)}[/latex]
[latex]\overrightarrow{v}_{f(120+85)}\text{= 1306 Ns ÷ 205 kg}[/latex]
[latex]\overrightarrow{v}_{f(120+85)}\text{= 6.4 m/s 51º North from East}[/latex]
EXAMPLE 9.3.2
Accident investigators are analyzing a car crash to see if excessive speed was involved. One of the cars had a mass of 1250 kg and was traveling at 40 km/h East when it was struck by a 1600 kg pickup truck that ran a red light, traveling South. If the wreckage moved at 23.5° East from South, should the truck driver also be charged for driving above the 60 km/h speed limit?
First, draw a sketch of the two vehicles:
All that is known are the mass of the two colliding vehicles, original velocity of the car and the angle at which the wreck moved off.
Combining this data, we can calculate the momentum of the car, and by using trigonometry we can calculate the momentum of the truck. The momentum of the truck allows us to estimate the initial velocity at which it was traveling.
First: The momentum of the car.
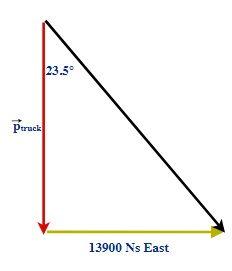
[latex]\overrightarrow{p} = m\overrightarrow{v}[/latex]
[latex]\overrightarrow{p}\text{= (1250 kg)(11.1 m/s East)}[/latex]
[latex]\overrightarrow{p}\text{= 13 900 Ns East}[/latex]
Now:
Using the Tangent function
[latex]\text{Tan 23.5º} =\dfrac{13 900 Ns}{\overrightarrow{p}_{truck}}[/latex]
[latex]\overrightarrow{p}_{truck}=\dfrac{13 900 Ns}{Tan 23.5º}[/latex]
[latex]\overrightarrow{p}_{truck}\text{= 32 00 Ns South}[/latex]
Finally, the velocity of the truck is
[latex]\overrightarrow{p}\text{= m v}[/latex]
[latex]\overrightarrow{v}\text{= (32 000 Ns South) ÷ (1600 kg)}[/latex]
[latex]\overrightarrow{v}\text{= 20 m/s South or 72 km/h}[/latex]
The truck was speeding by 12 km/h and could also be charged with speeding.
QUESTIONS 9.4 Two Dimensional Collisions
1. A 85 kg fullback is running at 9.0 m/s South and is tackled by a 70 kg halfback running at 8.0 m/s West. At what velocity do these two move after the tackle occurs?
2. Two hockey players collide mid-ice in a race for a puck. If the smaller player (80 kg) is racing at 12 m/s North and the larger player (90 kg) is racing at 15 m/s at 40° West from North, at what angle do the colliding players move off?
QUESTION 9.4.1 Survival Rates of Seat Areas in an Airplane 1971-2007
Question: Why is the greatest survival rate at the rear of the airplane?

QUESTION 9.4.2 Bullet Proof Vests
Bullet Proof Vests were first developed by Casimir Zeglen, a Catholic priest who in 1893 created a vest made from silks that was capable of stopping bullets. The principle behind these vests was to stop the bullet, causing it to deform, which then spread the bullet’s point of impact over a much larger area on the vest. Zeglen chose silk for the vest after reading a physician’s description of a man who had been shot but was saved by a silk handkerchief in his breast pocket. Soon tests were done by folding layers of silk some 10 to 30 times. Zeglen’s original vests used multiple layers of silk combined with an unknown chemical that he never disclosed. His later vests included blends of Angora and silk threads for handgun protection and even a steel sheet insert that worked to stop rifle bullets. His finished product was a cloth that was a little over 0.3 cm thick.

The above photo is taken from the May 1924 Popular Mechanics article showing a test subject being fired upon with 38 caliber (largest mass of 9.53 g, speed of 270 m/s) and 45 caliber (largest mass of 15 g, speed of 255 m/s) handguns.
Question: For the man in this photo, if we assume a mass of 68 kg (150 lb man), what should be his recoil velocity in stopping a 45 caliber bullet?
REFERENCES
1. Mechanical Universe – Episode 15 – Conservation of Momentum: https://www.youtube.com/watch?v=B44InZz-_pE
2. A-Level Physics Tutor: http://www.a-levelphysicstutor.com/index-mech.php
3. Extra Help – The Law of Momentum Conservation: https://www.physicsclassroom.com/class/momentum/Lesson-2/The-Law-of-Action-Reaction-(Revisited)
4. There are other physics conservation laws that exist in the study of particle physics.
5. Extra Help – Real World Applications: https://www.physicsclassroom.com/class/momentum/Lesson-1/RealWorld-Applications
6. Extra Help – The Law of Momentum Conservation: https://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle
7. Research News – Two neutron stars collided near the solar system billions of years ago: https://phys.org/news/2019-05-neutron-stars-collided-solar-billions.html
8. Extra Help – Isolated System: https://www.physicsclassroom.com/Class/momentum/u4l2c.cfm
9. Auto polo (1911 to late 1920‘s) was a motorsport that used similar rules to equestrian polo but used automobiles instead. Source: https://en.wikipedia.org/wiki/Auto_polo
10. Article to Read – A big space crash likely made Uranus lopsided: https://phys.org/news/2018-12-big-spaceuranus-lopsided.html
11. Article to Read – Uranus has experienced a colossal pounding: http://www.iflscience.com/space/uranusexperienced-a-colossal-impact-that-knocked-it-on-its-side/

