Chapter 11: Conservation of Mechanical Energy

Equations Introduced for this Topic (all solutions are scalars):
In an Isolated System, Mechanical Energy can be Conserved:
Energy Before = Energy After
For Mechanical Energy this means:
Eki + Epi = Ekf + Epf
½ mvi2 + mghi = ½ mvf2 + mghf
Since external forces can change the energy of a system, the only forces we are looking at in these problems is gravitational force, and we are assuming that frictional forces do not come into play.
Where:
W is Work, measured in Joules (J)
Ep or ∆Ep is Gravitational Potential Energy or change in Gravitational Potential Energy, measured in Joules (J)
Epi is the Initial Gravitational Potential Energy, measured in Joules (J)
Epf is the Final Gravitational Potential Energy, measured in Joules (J)
Eki is the Initial Kinetic Energy, measured in Joules (J)
Ekf is the Final Kinetic Energy, measured in Joules (J)
Ek or ∆Ek is Kinetic Energy or change in Kinetic Energy, measured in Joules (J)
V or Vg is the Gravitational Potential, measured in Newtons per Kilogram (N/kg)
m is the Mass of the object, measured in Kilograms (kg)
g or ag is the Gravitational Field Strength, measured in Metres per Second squared (m/s2)
v is the Speed of the object, measured in Metres per Second (m/s)
v or ∆v is the Speed or change in Speed of the object, measured in Metres per Second (m/s)
vf & vi is the final and initial Speed of the object, measured in Metres per Second (m/s)
[latex]\overrightarrow{F}_{net}[/latex] is the Net Force or the Vector Sum of the Forces acting on a body or a system, measured in Newtons (N)
ø is the angle between the vectors of the Net Force and Displacement, measured in degrees (°)
[latex]\overrightarrow{d}[/latex] is the displacement through which the Net Force acts on a body or a System, measured in Metres (m)
h or ∆h is the height or change in Vertical Height, measured in Metres (m)
hf & hi is the final and initial height of the object measured in Metres (m)
[latex]\overrightarrow{p}[/latex] Momentum is the product of Mass times Velocity and is measured in either Newton-Seconds (Ns) or Kilograms Metres per Second (kg m/s)
Notes
Work and Energy are measured in Joules (J) or Newton-Metres (Nm)
The Dot Product “ • “ represents the cosine of the angle between two vectors. For Work, it represents the angle between the direction of the Net Force and the displacement change.
The Cross Product “x “ represents the sine of the angle between two vectors. Equations using the cross product, such as the measure of Torque or the force on a charged particle moving in a magnetic field, will be given later in your study of physics.
For Example: Consider the following multiplication of these two vectors shown below:
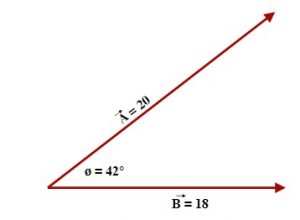
[latex]\overrightarrow{A}•\overrightarrow{B} =\overrightarrow{A}\overrightarrow{B}[/latex] cos Ø
[latex]\overrightarrow{A}•\overrightarrow{B}[/latex] = (20)(18) cos 42°
[latex]\overrightarrow{A}•\overrightarrow{B}[/latex] = 267.5 (≈ 270)
[latex]\overrightarrow{A}•\overrightarrow{B} =\overrightarrow{A}\overrightarrow{B}[/latex] sin Ø
[latex]\overrightarrow{A}•\overrightarrow{B}[/latex] = (20)(18) cos 42°
[latex]\overrightarrow{A}•\overrightarrow{B}[/latex] = 267.5 (≈ 240.9)
Kinetic Energy and Collisions: (WHO (2008) Speed Management Manual)
According to research, harmful injury is the result of ‘energy interchange’. During a collision, injury results from the transfer of energy to the human body in amounts and at rates that damage cellular structure, tissues, blood vessels and other bodily structures. This includes kinetic energy, for example when a motor vehicle user’s head strikes the windshield during a crash. Of the various forms of energy – kinetic, thermal, chemical, electrical and radiation – kinetic energy transfer is the biggest contributor to injury. It is useful for road traffic injury prevention researchers and practitioners to understand the biomechanics of kinetic energy injuries. This will help them develop measures that will limit the generation, distribution, transfer and effect of this energy during a road traffic collision.
(WHO (2008) Speed Management Manual)
ANU finds 530,000 potential pumped-hydro sites worldwide 4

WE NEED TO GET COPYRIGHT PERMISSION FOR ABOVE PICTURE
11.1 Conservation of Mechanical Energy 5, 6, 7
Energy(before) = Energy(after)
Eki + Epi = Ekf + Epf
Ep = mgh ∆Ep = mg∆h Ek = ½ mv2 ∆Ek = ½ m∆v2
∆h = hf – hi ∆v = vf – vi
In physics, mechanical energy refers only to gravitational potential and kinetic energy. In a system where an object is isolated from external, non-conservative forces, the mechanical energy will remain constant. This can be written as a conservation law, using conservative forces, and where the sum of the kinetic and potential energies after an event will remain constant.
Written in an equation, the conservation of Mechanical Energy looks like:
Eki + Epi = Ekf + Epf
This equation works for multiple bodies in a system. In real life, most forces acting on a system are non-conservative, with the classic example being friction. One of the main byproducts of non-conservative forces such as friction is heat, which is covered in a chapter later in this text/workbook.
Conceptual Origins
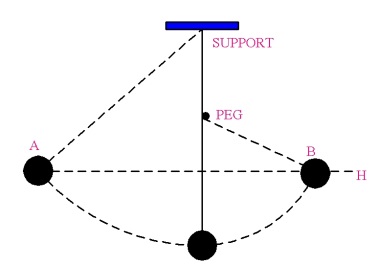
The history of the conservation of mechanical energy goes back as far as Thales of Miletus (c. 550 BCE) and Empedocles (490–430 BCE), who explored ideas relating to the conservation of mass-energy. Transitioning from the Greek philosophers, Simon Stevinus (1548–1620) used the principle that stated perpetual motion machines were impossible to create (non-conservative forces are always present and act to remove mechanical energy from a system). Galileo’s (1564-1642) interrupted pendulum8 was the first known classic example of conservation of mechanical energy. In this demonstration, where a pendulum is interrupted by a peg of some sort that shortens the length of the pendulum, the pendulum will rise to nearly the same height from which it was released. This pendulum example is generally introduced in detail in the next physics course, which explains this motion in terms of kinetic and potential energy, momentum and impulse, force, torques and free body diagrams.
The development of the conservation of mechanical energy is in reality the product of multiple scientists that followed, which extended energy conservation to heat, light and eventually Albert Einstein’s most famous: ∆E = mc2. The inclusion of heat and the First Law of Thermodynamics (energy cannot be created or destroyed, only transformed) are covered in following topics.
Examples of systems that are isolated and mainly experiencing conservative forces are pendulums and orbiting satellites, planets and comets where the main force that is acting is gravity. Examples and questions explored in this section will assume that non-conservative forces acting on a system will be non-existent or negligible.
EXAMPLE 11.1.1
If you were to shoot a crossbow bolt with a velocity of 75 m/s straight upwards, how high above its launch would the bolt travel?
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 m(75 m/s)2 + m(9.8 m/s2)(0 m) = 1/2 m(0 m/s)2 + m(9.8 m/s2)hf
Mass is common 1/2 (75 m/s)2 + 0 J = 0 J + (9.8 m/s2)hf
2812.5 J = (9.8 m/s2)hf
hf = 2812.5 J ÷ 9.8 m/s2
hf = 287 m (≈ 290 m)
(In the absence of air resistance)
EXAMPLE 11.1.2
Children take turns dropping from a treehouse that is 2.0 m above the ground. What would be the vertical velocity with which they would impact the ground?
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 m(0 m/s)2 + m(9.8 m/s2)(2.0 m) = 1/2 mvf2 + m(9.8 m/s2)(0 m)
Mass is common: 0 J + (9.8 m/s2)(2.0 m) = 1/2 vf2 + 0 J
1/2 vf2 = 19.6 m2/s2
vf2 = 39.2 m2/s2
vf = ± 6.26 m/s
Since velocity is asked for, the impact velocity is [latex]\overrightarrow{v}_{f}[/latex] = – 6.26 m/s (≈ – 6.3 m/s)
EXAMPLE 11.1.3
A stuntman runs at 8.0 m/s off a 4.0 m vertical drop. At what speed does he impact the cushions stopping his fall at the bottom of the drop?
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 m(8.0 m/s)2 + m(9.8 m/s2)(4.0 m) = 1/2 mvf2 + m(9.8 m/s2)(0 m)
Mass is common: 32 m2/s2 + 39.2 m2/s2 = 1/2 vf2 + 0 J
71.2 m2/s2 = 1/2 vf2
vf2 = 142.4 m2/s2
vf = 11.9 m/s (≈ 12 m/s)
QUESTIONS
1. The Steamboat Geyser9 in Yellowstone is the world’s tallest currently active geyser. What
is the ejected velocity of the water if during a major eruption, the geyser can reach heights in excess of 91 m?

2. A paint bucket tipped over on a worker’s scaffold falls through a potential difference of
118 N/kg or (m2/s2 12 m drop) to strike a patio table below. At what speed does this paint
strike the table?
3. It is estimated that the medieval longbow could launch an arrow with a speed of 60 m/s. If we ignore the effects of air resistance, how high would these arrows travel if fired straight upwards?
4. A child climbs a tree house and drops her pet guinea pig to see if it could fly. If we assume the guinea pig fell about 2.5 m to the grass, with what impact speed would it strike the ground?
(Its impact speed was far less than this since she had a cape tied to her “Super Hammy”.)
5. A golf ball is launched with a speed of 125 km/h. At what speed is it traveling when it has
risen 40 m above its starting position?
6. Water flowing at 8.0 m/s flows off a 12 m vertical waterfall. At what speed does it impact
the base of the falls?
7. A 0.50 kg mass is projected horizontally with speed 8.0 m/s from the top of the cliff 45 m
high.
(i) What is the initial kinetic energy of the body?
(ii) What is its kinetic energy just before striking the ground?
8. A car drives off a 50 m high cliff at 90 km/h. At what speed should it reach before
impacting the base of the cliff?
9. A 2.2 kg projectile is fired upwards at an angle at 33 m/s. It gains a maximum height of
30.0 m above the level from which it was fired. Calculate:
(i) its initial kinetic energy;
(ii) its horizontal speed at maximum height.
10. A 17.34 kg mass has a total mechanical energy of 93 500 J when moving at a height of
360 m. What is its speed?
11. If a roller coaster is traveling at 75 km/h when it goes over a drop and falls through a
potential difference of 420 N/kg, what speed can it reach? Assume no external frictions act to slow it down.
12. If we assume that a cyclist is at the top of the Eshima Ohashi bridge in Japan traveling at
10 m/s, what speed could be reached if this cyclist rolls to the bottom through a potential
difference of 430 N/kg? (ignore all friction).


This photo is take through a telephoto lens and makes the bridge appear insanely steep. Optical illusion.
11.2 Non-Horizontally Launched Projectiles
Energy(before) = Energy(after)
Eki + Epi = Ekf + Epf
Ep = mgh ∆Ep = mg∆h Ek = ½ mv2 ∆Ek = ½ m∆v2
∆h = hf – hi ∆v = vf – vi
In some problems, projectiles launched at an angle can be solved with the conservation of mechanical energy instead of using trigonometry to break the motion into vector quantities of vertical and horizontal components to solve. Using mechanical energy greatly simplifies the solutions to these problems. In all of these problems, air resistance is not accounted for.
EXAMPLE 11.2.1
Consider a bottle of water thrown at 18 m/s at 30° above the horizontal from the edge of one balcony to be caught by a friend on another balcony 12 m below. At what speed would the friend catch the bottle of water?
Since we are using energy to solve this, we can skip using vectors and trigonometry
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 (m)(18 m/s)2 + (m)(9.8 m/s2)(12 m) = 1/2 (m)vf2 + (m)(9.8 m/s2)(0 m)
Mass is common. 1/2 (324 m2/s2) + (117.6 m2/s2) = 1/2 vf2 + 0 J
162 m2/s2 + 117.6 m2/s2 = 1/2 vf2 + 0 J
279.6 m2/s2 = 1/2 vf2
vf2 = 559.2 m2/s2
vf = 23.6 m/s (≈ 24 m/s)
EXAMPLE 11.2.2
A competitive archer shoots an arrow at 48 m/s angled at 35° above the horizontal from a castle rampart 25 m above the ground. At what speed would we expect this arrow to strike the ground if we ignore air resistance?
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 (m)(48 m/s)2 + (m)(9.8 m/s2)(25 m) = 1/2 (m)vf2 + (m)(9.8 m/s2)(0 m)
Mass is common. (1152 m2/s2) + (245 m2/s2) = 1/2 vf2 + 0 J
1397 m2/s2 = 1/2 vf2
vf2 = 2794 m2/s2
vf = 52.9 m/s (≈ 53 m/s)
EXAMPLE 11.2.3
A baseball player throws a ball into the stands with a velocity of 90 km/h angled at 40° above the horizontal. If this ball is caught by a fan that is 25 m above the height from which it was thrown, at what speed is it traveling?
Eki + Epi = Ekf + Epf
1/2 mvi2 + mghi = 1/2 mvf2 + mghf
1/2 (m)(25 m/s)2 + (m)(9.8 m/s2)(0 m) = 1/2 (m)vf2 + (m)(9.8 m/s2)(25 m
(m)(312.5 m2/s2) + (m)(0 m2/s2) = 1/2 (m)vf2 + (m)(245 m2/s2)
Mass is common. 312.5 m2/s2 – 245 m2/s2 = 1/2 vf2
vf2 = 135 m2/s2
vf = 11.6 m/s (≈ 12 m/s)
QUESTIONS 11.2 Non-Horizontally Launched Projectiles
1. Firefighters are directing a water stream of 53 m/s upwards at 32° above the horizontal.
What is the speed of this water 16 m above where it is launched?

2. If someone throws a first aid kit at 8.2 m/s downwards at 28° below the horizontal, what
should its speed be if caught by a person 9.0 m below where it was thrown?
3. An archer shoots an arrow at 60 m/s at an angle of 45° above the horizontal from the top of a cliff. At what speed should the arrow strike the field 48 m below where the arrow was
launched?
4. A football player throws a football into the stands at a velocity of 21 m/s angled at 50°
above the horizontal. If this football is caught by a fan that is 18 m above the height from
where it was thrown, at what speed is it traveling?
11.3 Elastic and Inelastic Collisions 9
Equations Used in this Section:
In an Isolated System,
[latex]\Sigma\overrightarrow{p}[/latex] = constant
or …
[latex]\overrightarrow{p}_{before} =\overrightarrow{p}_{after}[/latex] (Vector Equation)
Where …[latex]\overrightarrow{p} = m\overrightarrow{v}[/latex]
And …
Energy(before) = Energy(after)
Eki + Epi = Ekf + Epf
Ep = mgh ∆Ep = mg∆h Ek = ½ mv2 ∆Ek = ½ m∆v2
∆h = hf – hi ∆v = vf – v
Concepts used in this Section:
Collisions must always obey the Law of Conservation of Momentum. That is, the vector sum of momenta prior to a collision equals the vector sum after a collision carrying a requirement that no external forces are acting on the colliding objects. However, collisions are classified due to kinetic energy being or not being conserved in the collision.
Collisions where some of the initial kinetic energy is turned into heat or some other form of energy are inelastic. Collisions where kinetic energy is not lost are classified as elastic. Collisions between atoms10 in ideal gases are generally elastic since no kinetic energy is lost during the collision. Other examples of elastic collisions are the scattering of sub-atomic particles when deflected by electromagnetic forces or the gravitational interactions between planets and satellites11. Inelastic collisions are further differentiated if they lose all kinetic energy during the collision or only part of the initial kinetic energy. In collisions where all kinetic energy is lost the collision is classified as perfectly inelastic. For collisions where only some of the kinetic energy is lost, the collision is defined as partially elastic or inelastic.
Summing this up:
• Perfectly elastic collisions conserve both momentum and kinetic energy.
• Partially elastic collisions or inelastic conserve momentum and some kinetic energy.
• Perfectly inelastic collisions conserve only momentum and lose all kinetic energy.

Generally, macroscopic collisions are partially elastic or perfectly inelastic. Newton’s cradle12 is one apparatus that comes close to a perfectly elastic collision and is used for demonstrations in introductory physics classes.
Observers watching a demonstration of Newton’s cradle can hear the sound of the metal balls colliding, which acts to extract energy out of the collision, so it becomes quite obvious that the collision is not perfectly elastic.
The following examples explore the elasticity of collisions.
EXAMPLE 11.3.1
Two objects collide on a frictionless surface. The first object, having a mass of 4.0 kg, has a velocity of 2.0 m/s prior to the collision and – 5.2 m/s after. The second object, having a mass of 6.0 kg, has a velocity of – 4.0 m/s prior to the collision and 0.8 m/s after. Verify that this collision could exist and identify what type of a collision it is. (Perfectly Elastic, Partially Elastic or Inelastic, or Perfectly Inelastic).
Data: First solve for the velocity of mass 2 [latex]\overrightarrow{v}_{2f}[/latex] before the collision.
m1 = 4.0 kg
[latex]\overrightarrow{v}_{1i}[/latex] = 2.0 m/s [latex]\overrightarrow{p}_{before} =\overrightarrow{p}_{after}[/latex]
[latex]{v}_{1f}[/latex] = – 5.2 m/s
m2 = 6.0 kg or: [latex]m_{1}\overrightarrow{v}_{1i} + m_{2}\overrightarrow{v}_{2i} = m_{1}\overrightarrow{v}_{1f} + m_{2}\overrightarrow{v}_{2f}[/latex]
[latex]\overrightarrow{v}_{2i}[/latex] = – 4.0 m/s
[latex]\overrightarrow{v}_{2f}[/latex] = 0.8 m/s Inputing variables yields:
(4.0 kg)(2.0 m/s) + (6.0 kg)(- 4.0 m/s) = (4.0 kg)(-5.2 m/s) + (6.0 kg)(0.8 m/s)
8.0 Ns – 24 Ns = – 20.8 Ns + 4.8 Ns
16 Ns = 16 Ns … Momentum is conserved
Now check to see if any Kinetic Energy was lost during the collision:
Eki = Ekf
or: 1/2m1 v1i2 +1/2m2 v2i2 = 1/2m1 v1f2+1/2m2 v2f2
Inputing variables yields:
1/2 (4.0 kg)(2.0 m/s)2 + 1/2 (6.0 kg)(- 4.0 m/s)2 = 1/2 (4.0 kg)(-5.2 m/s)2 + 1/2 (6.0 kg)
(0.8 m/s)2
8.0 Nm + 48 Nm = 54.08 Nm + 1.92 Nm 56 Nm = 56 Nm Kinetic Energy is conserved
Because Kinetic Energy was conserved, this collision is an example of a perfectly elastic collision.
NOTE IN THE PDF it is Nm…In the WORD document it becomes J ???
EXAMPLE 11.3.2
Two objects collide on a frictionless surface. The first object, having a mass of 0.42 kg, has a velocity of – 0.32 m/s prior to the collision and 0.26 m/s after. The second object has a mass of 0.88 kg at an unknown velocity prior to the collision and at rest after. Find the velocity and identify what type of a collision it is. (Perfectly Elastic, Partially Elastic or Inelastic, or Perfectly Inelastic).
Data
First solve for the velocity of mass 2[latex](\overrightarrow{v}_{2f})[/latex] before the collision.
m1 = 0.42 kg
[latex]\overrightarrow{v}_{1i}[/latex]= – 0.32
m/s [latex]\overrightarrow{p}_{before} =\overrightarrow{p}_{after}[/latex]
[latex]\overrightarrow{v}_{1f}[/latex]= 0.26 m/s
m2 = 0.88 kg or: [latex]m_{1}\overrightarrow{v}_{1i} + m_{2}\overrightarrow{v}_{2i} + m\overrightarrow{v}_{1f}m_{2}\overrightarrow{v}_{2f}[/latex]
[latex]\overrightarrow{v}_{2i}[/latex] = 0 m/s
[latex]\overrightarrow{v}_{2f}[/latex] = Unknown Inputing variables yields:
(0.42 kg)(- 0.32 m/s) + (0.88 kg)([latex]\overrightarrow{v}_{2f}[/latex]) = (0.42 kg)(0.26 m/s) + (0.88 kg)(0 m/s)
– 0.1344 Ns + (0.88 kg)[latex](\overrightarrow{v}_{2f})[/latex]) = 0.1092 Ns + 0 Ns
(0.88 kg)([latex]\overrightarrow{v}_{2f})[/latex] = 0.2436 Ns
[latex]\overrightarrow{v}_{2f}[/latex] = 0.2436 Ns / 0.88 kg
[latex]\overrightarrow{v}_{2f}[/latex] = 0.277 m/s
Now check to see if any Kinetic Energy was lost during the collision:
Eki = Ekf
or: 1/2 m1 v1i2 + 1/2 m2 v2i2 = 1/2 m1 v1f2 + 1/2 m2 v2f2
Inputing variables yields:
1/2(0.42 kg)(- 0.32 m/s)i2 + 1/2(0.88 kg)(0.277 m/s)i2 = 1/2(0.42 kg)(0.26 m/s)i2 + 0 Nm
0.0215 J + 0.0338 J = 0.0142 J + 0 J
0.0553 N J m = 0.0142 J … Kinetic Energy is lost
Because Kinetic Energy was not conserved, this collision is an example of an inelastic collision.
QUESTIONS 11.3 Elastic and Inelastic Collisions
1. A 0.50 kg billiard ball traveling at 1.5 m/s strikes a 0.45 kg billiard ball at rest. If the 0.50 kg ball slows to 0.75 m/s, at what speed is the 0.45 kg ball moving? What type of elastic collision is this?
2. Two balls of putty sliding towards each other collide and come to a complete stop. If the small ball had a mass of 150 g and a velocity of 12.0 cm/s North prior to the collision, what was the velocity of the 200 g larger ball prior to the collision? What type of elastic collision was this?
3. Two balls of identical mass (0.500 kg), each having a kinetic energy of 3.0 Joules, are directed toward each other. During the collision each experience equal and opposite impulses of 2.0 Nm.
(i) What were their speeds prior to the collision?
(ii) What are their speeds after the collision?
(iii) Was this collision elastic or inelastic?
(iv) What impulse would be needed to make this a perfectly elastic collision?
11.4 Work, Force & Change in Energy Problems – Launching and Braking Devices13
Equations Used in the Section:
Work (W) =[latex]\overrightarrow{F}_{net}•\overrightarrow{d}\text{or }\overrightarrow{F}_{net}\overrightarrow{d}[/latex] cos Ø W = ∆ Mechanical Energy
Ep = mgh ∆Ep = mg∆h Ek = ½mv2 ∆Ek = ½m∆v2
∆h = hf – hi ∆v = vf – vi V or Vg = gh
Concepts used in this section:
When one is using the work-energy theorem in situations where only conservative forces are acting, then W = ∆Ek or W = (Ek f – Ek i). Under some conditions, the work done on a system can result in a change in both potential and kinetic energy W = ∆Ek + ∆Ep. This equation is not defined by the work-energy theorem but is a combination of the work-energy theorem and the conservation of mechanical energy. In these cases work can be seen as the function of adding or subtracting energy from the system, using the conservation of mechanical energy to define the total energy of the system, which could be converted to a kinetic energy.
EXAMPLE 11.4.1
A 1400 kg car is traveling at 45 km/h at the top of a 42 m high hill.
(i) What amount of work is needed to stop this car at the bottom of the hill?
W = ∆Ek + ∆Ep
W = (Ekf – Eki) + (Epf – Epi)
W = 1/2 mvf2 – 1/2 mvi2 + mghf – mghi
W = 1/2(1400 kg)(0 m/s)2 – 1/2(1400 kg)(12.5 m/s)2
+ (1400 kg)(9.8 m/s2)(0 m) – (1400 kg)(9.8 m/s2)(42 m)
W = 0 J – 109 375 J + 0 J – 576 240 J
W = – 686 000 J (≈ – 690 000J)
(ii) What average braking force is needed to do this if the car stops in 200 m at the bottom of this hill?
W = ∆ Energy
For this car: W = – 686 000 J
Now: [latex]\overrightarrow{F}\overrightarrow{d}[/latex] cos ø = – 686 000 J
[latex]\overrightarrow{F}[/latex] (200 m) cos 0° = – 686 000 J
[latex]\overrightarrow{F}[/latex] = – 686 000 J ÷ 200 m
[latex]\overrightarrow{F}[/latex] = – 3430 N
EXAMPLE 11.4.2
A co-worker tosses a 4.0 kg brick to his friend 2.0 m below at 1.5 m/s. What amount of force is needed to catch and stop this brick in a horizontal distance of 0.50 m?
First, find out how much energy needs to be removed from the brick when catching it.
W = ∆Ek + ∆Ep
W = (Ekf – Eki) + (Epf – Epi)
W = 1/2 mvf2 – 1/2 mvi2 + mghf – mghi
W = 1/2(4.0 kg)(0 m/s)2 – 1/2(4.0 kg)(1.5 m/s)2
+ (4.0 kg)(9.8 m/s2)(0 m) – (4.0 kg)(9.8 m/s2)(2.0 m)
W = 0 J – 4.5 J + 0 J – 78.4 J
Second, Find out the average braking force needed to do this in 0.5 m.
For the brick:
W = – 82.9 J
Now, [latex]{F}\overrightarrow{d}[/latex] cos ø = – 82.9 J
[latex]\overrightarrow{F}[/latex](0.5 m) cos 0° = – 82.9 J
[latex]\overrightarrow{F}[/latex]F = – 82.9 J ÷ 0.5 m
[latex]\overrightarrow{F}[/latex] = – 166 N (≈-170 N)
QUESTIONS 11.4 Work, Force and Change in Energy Problems – Launching and Braking Devices
1. A 35 kg bag of sand swings from the end of a 3.2 m long rope. It is drawn back from its vertical position to the horizontal then released.
(i) What speed does it have at the bottom of its swing?
(ii) A mechanical catching device brings it to a full stop (in 0.10 m) at the bottom of the swing. How much work is done by the device?
(iii) What braking force is needed to stop the sand bag?
2. What is the average force that a circus cannon exerts on a 75 kg stunt person over the 2.0 m they are launched with, so that the stunt person is traveling at 3.0 m/s when 5.0 m above the launched height?
3. A 4200 kg truck is rolling along at 80 km/h at the top of a 102 m high hill. If this truck is allowed to freely accelerate to the bottom of the hill before the brakes are applied, what average braking force would be needed to stop this truck in half a kilometre?
QUESTIONS 11.5.1 A Trebuchet Catapult
A Trebuchet Catapult is capable of launching 140 kg stones with such energy they will still be traveling at 80 km/h when 60 m above the original launch height.

Question: At what speed are these stones released?
A trebuchet or trebucket is a siege engine that was employed in the Middle Ages either to smash masonry walls or to throw projectiles over them. It is sometimes called a “counterweight trebuchet” or “counterpoise trebuchet” in order to distinguish it from an earlier weapon that has come to be called the “traction trebuchet”, the original version with pulling men instead of a counterweight. The counterweight trebuchet appeared in both Christian and Muslim lands around the Mediterranean in the twelfth century. It could fling three-hundred-pound (140kg … largest appear to be 1500 kg) projectiles at high speeds into enemy fortifications. On occasion, disease-infected corpses were flung into cities in an attempt to infect the people under siege a medieval variant of biological warfare. Traction trebuchets appeared in China in about the 4th century BC and in Europe in the 6th century AD, and did not become obsolete until the 16th century, well after the introduction of gunpowder. Trebuchets were far more accurate than other medieval catapults. Adapted from … http://en.wikipedia.org/wiki/Trebuchet
QUESTIONS 11.5.2 Kingda Ka … Six Flags Great Adventure
On May 21, 2005, Six Flags Great Adventure introduced Kingda Ka the tallest and fastest roller coaster on the planet to the public. This Swiss designed “rocket coaster” uses hydraulic motors to launch the cars along a horizontal section of track from zero to 205 km/h in an impressive 3.5 seconds. The cars then begin a vertical ascent up a steel tower that peaks at 139 m or 45 stories. Crossing over the apex the train enters a vertical descent plunging through a 270° spiral twist again reaching speeds more than 160 km/h. One final surprise comes before the brake run – a 39 m tall camelback hill that offers plenty of negative g’s also known fondly as “airtime”.

Question: With its launch speed of 205 km/h, how fast could this roller coaster be moving after it has climbed a vertical height of 139 m? (It will be less than this due to friction.)
QUESTIONS 11.5.3 The Ballistic Pendulum
The Ballistic Pendulum was invented in 1742 by English mathematician Benjamin Robins (1707-1751) and published in his book New Principles of Gunnery, which revolutionized the science of ballistics as it provided the first way to accurately measure the velocity of a bullet. Robins used the ballistic pendulum to measure projectile velocity in two ways. The first was to attach the gun to the pendulum and measure the recoil. Since the momentum of the gun is equal to the momentum of the ejecta and since the projectile was (in those experiments) the large majority of the mass of the ejecta the velocity of the bullet could be approximated. The second and more accurate method was to directly measure the bullet momentum by firing it into the pendulum and measuring the change in potential energy of the pendulum + embedded bullet.
Question: Suppose one wanted to set up a ballistics pendulum to check the muzzle velocity of a bullet fired from an 1894 Winchester (30-30) as shown below. Specs show that it should shoot an 8.0 g (130 grain) bullet at 759 m/s. What mass of wooden block would be needed so that it would rise 10.0 cm above its rest position after being struck by this bullet?
REFERENCES:

