Chapter 4: Vertical Motion

Equations Used for this Topic (all equations can be written and solved as both scalar and vector and all variables are the same measures and units as chapter 3):
For Terminal Velocity (a = 0) [latex]v =\dfrac{\Delta{d}}{t}[/latex]
For Free Fall (a = g or ag which equals -9.80 m/s2)
[latex]a =\dfrac{\Delta{v}}{t}[/latex]
[latex]\Delta{v}= v_f - v_i[/latex] [latex]v=\dfrac{(v_i + v_f)}{2}[/latex]
vf = vi + at 2ad = vf2- vi2
[latex]d = v_t + ½at{^2}[/latex] [latex]d=\dfrac{(v_i + v_f)t}{2}[/latex]
Where...
v is Average Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}[/latex] is Average Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vi is Initial Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/s)
[latex]\overrightarrow{v}_i[/latex] is Initial Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/s) and includes a direction
vf is Final Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/s)
[latex]\overrightarrow{v}_f[/latex] is Final Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/s) and includes a direction
[latex]\Delta{d}[/latex] is Distance travelled, commonly measured in Metres (m), Kilometers (km)
[latex]\Delta\overrightarrow{d}[/latex] Is Change in Displacement, commonly measured in Metres (m), Kilometres (km) and includes a direction
a is Acceleration (deceleration is negative), measured in Metres per Second squared (m/s2)
[latex]\overrightarrow{a}[/latex] is Vector Acceleration, measured in Metres per Second squared (m/s2) and includes a direction
t is Time, commonly measured in Second (s) or Hours (h)
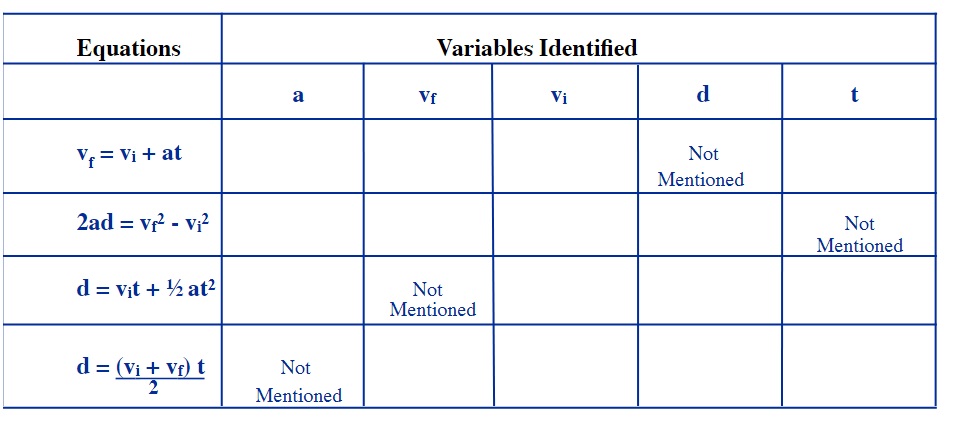
Vector Conventions for Vertical Motion
When working with vertical motion problems, vector analysis and solutions are the preferred approach and will eliminate minor issues that result from scalar solutions. Vertical motion vectors are simple in direction: up is positive and down is negative.
The following sketch shows these vector conventions and their respective zero points.
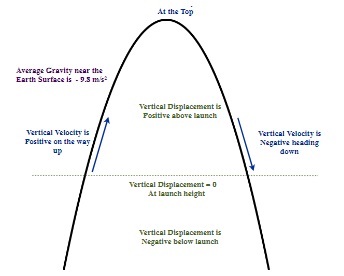
As air resistance begins to increase in strength, the net acceleration downwards also increases until it is approximately zero. More advanced classes would use calculus to calculate the motion occurring during this changing acceleration. The scope of this course does not ask you to analyse these types of problems.
4.1 Vertical Motion in One Direction
For all falling objects, during the first few seconds of fall air resistance is negligible (we call this Free Fall Motion5, 6) and the object accelerates downwards at the acceleration rate due to gravity7, a = g or ag which equals - 9.80 m/s2.

Vertical Motion problems are most commonly solved using vectors with the following conventions:
• All vectors directed upwards are termed positive
• All vectors directed downwards are termed negative
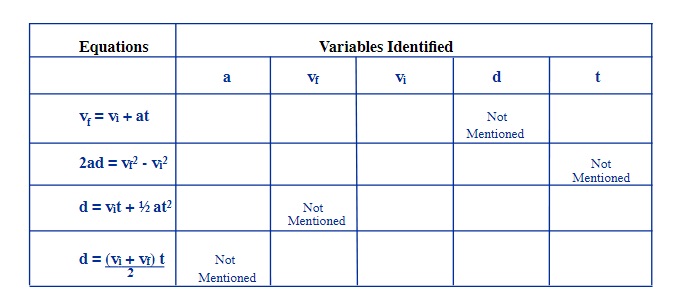
The equations used to solve vertical motion problems are the same equations used in the previous Chapter 3 and are as follows:
[latex]\overrightarrow{a}=\dfrac{\Delta\overrightarrow{v}}{t}[/latex] [latex]\Delta\overrightarrow{v}=\overrightarrow{v}_f\overrightarrow{v}_i[/latex] [latex]\overrightarrow{d}=\dfrac{(\overrightarrow{v}_i +\overrightarrow{v}_f)t}{2}[/latex]
[latex]\overrightarrow{d}=\overrightarrow{v}_it +\dfrac{1}{2}\overrightarrow{a}t{^2}[/latex] [latex]2\overrightarrow{a}\overrightarrow{d} =\overrightarrow{v}_f{^2} -\overrightarrow{v}_i{^2}[/latex] [latex]\overrightarrow{v}_f =\overrightarrow{v}_i +\overrightarrow{a}t[/latex]
To solve these problems, you will use exactly the same definition of terms and equations, and the chart to decide which equation will lead you to a solution is repeated for you on the next page. The one major difference is for acceleration. In any free fall motion, the falling object will be accelerating downwards at 9.8 m/s2 and is generally used in its vector form as - 9.8 m/s2. This acceleration remains constant until air resistance becomes large enough to slow the net acceleration downwards.
Once air resistance is great enough the object reaches Terminal Velocity 8 (where anet = 0) and the objects fall at a constant speed or velocity. Terminal velocity is due to the net force acting on the falling object being balanced out to zero and occurs when the force of gravity pulling the falling object downwards is balanced by the air resistance the object encounters.
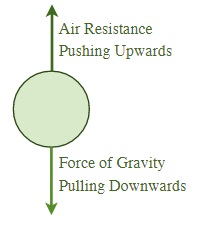
Some unique features about falling objects:
• Most falling objects reach a terminal velocity within a few seconds, after which they fall at a constant velocity downwards.
• As the object gets closer to the Earth, air density increases and the object will actually slow down in their descent.
After the object reaches its terminal velocity, solving any question about its velocity uses the equations from Chapter 2:
[latex]\overrightarrow{v}=\dfrac{\Delta\overrightarrow{d}}{t}[/latex]
Terminal Velocity questions are similar to questions given in Chapter 2, except they all involve falling at a constant rate and the objects are no longer accelerating.
Historical Development
The study of falling bodies presented a significant challenge to the early philosophers trying to study the motion. This problem is twofold, the first aspect being the rate of distance the object falls. For distance, an object falls around 4.9 m in 1 s and for 2 s of free fall, and this distance increases to a little under 20 m. The second aspect is the effect of air resistance on a falling body. It only takes a few seconds for air resistance to significantly affect the rate at which an object is falling and as such, trying to understand the nature of falling objects becomes challenging.
Aristotle, one of the most significant of the Greek philosophers to work to understand falling objects, observed objects falling through water. This means that the terminal velocity of any object was reached in a fraction of a second, unless the mass of the object was large enough to help reduce the overall impact of air resistance. His conclusions that heavier objects fell faster than lighter objects was illustrated by these observations. Also, if looking at fluids9 falling through water, the net density of the fluid meant that the fluid would float or sink. This he interpreted to mean that the rate of motion depended on the amount of earth or water in the fluid. Logically, Aristotle’s model of the universe was compelling.
Most of Aristotle's works were lost, with only 31 of nearly 200 currently known. Historians believe that these surviving works were lecture notes that he used when teaching at the Plato’s Academy and the Lyceum. The collection of his notes that refers to animals, cosmology, physics and metaphysics was combined into what became known as the Organon. Within two decades after Aristotle’s death, his influence on Greek philosophy appears to have disappeared. The 31 known collections of Aristotle’s writings were all that was found in a moldy cellar some 300 years later. They were grouped and edited, and distributed throughout Middle East, where they were taught with varying impact over the next 1100 years. The medieval Catholic Church adopted much of Aristotelean philosophy in the early 1300s, until the works of Galileo subjected them to greater scrutiny.
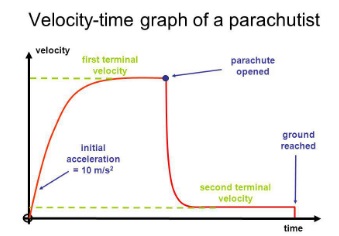
When trying to interpret falling objects in today's world, the fall of a parachutist provides some excellent data. In free fall, a parachutist would reach a terminal velocity of around 50 m/s in about 5 s. In reality, it takes about 10 s for the parachutist to reach this speed. After about 10 s, the parachutist is falling at terminal velocity, and remains so until the parachute is opened. At this point, the deceleration is rapid until the second terminal velocity of floating to the surface is reached. The terminal velocity in both cases is altered by the angle of the parachutist when falling (this changes the resistance of the air) and of increasing air density as the person nears the Earth's surface.
Let's consider using these constant acceleration equations and vector conventions for free-fall problems (no air resistance) in the following examples 10, 11 [footnotes?]
EXAMPLE 4.1.1
A pebble dropped from a bridge is observed to strike the water after 4.2 s of free fall. (i) What is the impact velocity of this pebble? (ii) What is the distance this pebble fell?
Data (i)
| [latex]\overrightarrow{a}= - 9.8\text{m/s}{^2}[/latex] | [latex]\overrightarrow{v}_f=\overrightarrow{v}_i + at[/latex] |
|---|---|
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]\overrightarrow{v}_f=0 m/s + -9.8 \text{m/s}{^2})[/latex] |
| [latex]\overrightarrow{v}_f = find[/latex] | [latex]\overrightarrow{v}_f=-41.2\text{m/s} (\approx- 41\text{ m/s)}[/latex] |
| [latex]\overrightarrow{d}= No[/latex] | [latex]\overrightarrow{v}_f=-41.2\text{m/s}(\approx - 41\text{ m/s)}[/latex] |
| t = 4.2 s |
[latex]\overrightarrow{a}= - 9.8 m/s{^2}[/latex] [latex]\overrightarrow{v}_f =\overrightarrow{v}_i + at[/latex]
[latex]\overrightarrow{v}_i = 0 m/s[/latex] [latex]\overrightarrow{v}_f = 0 m/s + (-9.8 m/s{^2})[/latex]
[latex]\overrightarrow{v}_f = find[/latex] [latex]\overrightarrow{v}_f = -41.2 m/s (\approx- 41 m/s)[/latex]
[latex]\overrightarrow{d}= No[/latex] [latex]\overrightarrow{v}_f = - 41.2 m/s (\approx - 41 m/s)[/latex]
t = 4.2 s
Data (ii)
| [latex]\overrightarrow{a}= -9.8 m/s{^2}[/latex] | [latex]\overrightarrow{d}=\overrightarrow{v}_it +\dfrac{1}{2}\overrightarrow{a}t{^2}[/latex] |
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]\overrightarrow{d}= (o m/s)(4.2 s) +½(-9.8 m/s)(4.2 s){^2}[/latex] |
| [latex]\overrightarrow{v}_f= No[/latex] | [latex]\overrightarrow{d}= 0 m - 86.4 m[/latex] |
| [latex]\overrightarrow{d}= find[/latex] | d = 86.4 m (≈ 86 m) |
| t = 4.2 s |
EXAMPLE 4.1.2
A flowerpot drops to the ground from a window ledge 10 m up. (i) What is the change in displacement of this flowerpot? (ii) What amount of time is needed for it to impact the ground?
(i) The change in displacement is - 10 m.
(ii) Data
| [latex]\overrightarrow{a}=-9.8 m/s{^2}[/latex] | [latex]d = v_it + 1/2 at{^2}[/latex] |
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]-10 m = 1/2 (-9.8 m/s{^2})t{^2}[/latex] |
| [latex]\overrightarrow{v}_f = No[/latex] | [latex]-10 m = -4.9 m/s{^2}t[/latex] |
| [latex]\overrightarrow{d}= - 10 m[/latex] | [latex]t^{2} = (- 10 m) ÷ (- 4.9 m/s^{2})[/latex] |
| [latex]t = find[/latex] | [latex]t{^2}= 2.04 s{^2}[/latex] |
| [latex]\overrightarrow{d}= - 10 m[/latex] |
EXAMPLE 4.1.3
A marker is dropped from a construction crane. (i) What is its velocity 2.0 s later? (ii) What was its change in displacement during these two seconds?
Data (i)
| [latex]\overrightarrow{a}= -9.8\text{ m/s}{^2}[/latex] | [latex]\overrightarrow{v}_f = v_i + at[/latex] |
| [latex]\overrightarrow{v}_i = 0\text{ m/s}[/latex] | [latex]v_f = 0\text{ m/s} + (- 9.8\text{ m/s}{^2})[/latex] |
| [latex]\overrightarrow{v}_f = find[/latex] | |
| [latex]v_f= - 19.6\text{ m/s} (\approx- 20\text{ m/s})[/latex] | |
| [latex]\overrightarrow{d} = No[/latex] | |
| t = 2.0 s |
Data (ii)
| [latex]\overrightarrow{a}= - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{d}\overrightarrow{v}_it =½\overrightarrow{a}t{^2}[/latex] |
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]\overrightarrow{d}= (0 m/s)(2.0 s) +½ (- 9.8 m/s^{2})(2.0 s)^{2}[/latex] |
| [latex]\overrightarrow{v}_f = No[/latex] | [latex]\overrightarrow{d}= 0 m - 19.6[/latex] |
| [latex]\overrightarrow{d}= find[/latex] | [latex]\overrightarrow{d}= - 19.6 m[/latex] |
| t = 2.0 s |
The change in displacement is found by:
[latex]\overrightarrow{d}=\overrightarrow{d}_f -\overrightarrow{d}_i[/latex]
Therefore:
[latex]\overrightarrow\Delta{d}= - 19.6 m - 0 m[/latex]
[latex]\overrightarrow\Delta{d} = - 19.6 m (\approx - 20 m)[/latex]
EXAMPLE 4.1.4
What must be the initial launch velocity of a baseball for it to reach a maximum vertical displacement of 42 m?
Data:
| [latex]\overrightarrow{a}= - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{2}ad =\overrightarrow{v}_f{^2}-\overrightarrow{v}_i{^2}[/latex] |
| [latex]\overrightarrow{v}_i = find[/latex] | [latex]2 (-9.8 m/s{^2}) (42 m) = (0 m/s){^2} -\overrightarrow{v}_i{^2}[/latex] |
| [latex]\overrightarrow{v}_f = 0 m/s[/latex] | [latex]- 823.2 m{^2}/s{^2} = -\overrightarrow{v}_i{^2}[/latex] |
| [latex]\overrightarrow{d}= 42 m[/latex] | [latex]\overrightarrow{v}_i{^2} = 823.2 m{^2}/s{^2}[/latex] |
| [latex]\overrightarrow{t}= No[/latex] | [latex]vi= \underline{+} 28.7 m/s[/latex] |
| Choose [latex]\overrightarrow{v}_i = + 28.7 m/s(\approx + 29 m/s)[/latex] |
Note:
When taking the square root for this problem the solution is ± 28.7 m/s. This means that you must interpret the correct vector direction of this number. For this problem the correct vector direction is positive (or upwards).
QUESTIONS 4.1 Vertical Motion in One Direction
- A pebble dropped from a bridge is observed to strike the water after 2.5 s of free fall. (i) What is the impact velocity of this pebble? (ii) What is the distance this pebble fell?
- A flowerpot drops to the ground from a window ledge 20 m above. (i) What is the change in displacement of this flowerpot? (ii) What amount of time is needed for it to impact the ground?
- A bag of flour is dropped from a helicopter. (i) What is its velocity 3.0 s later. (ii) What distance did it fall during these three seconds?
- The Empire State building is 449 m high. (i) How long would it have taken King Kong to fall from it? (ii) What would be his impact velocity?

King Kong poster author unknown under the public domain - What must be the initial launch velocity of a baseball for it to reach a maximum vertical displacement of 30 m?6 [footnote?]. During the construction of the IDS Tower in downtown Minneapolis, an electrician accidentally dropped a slug (from an electrical outlet box) off the 57th floor. This slug fell to the ground and punched a hold through the roof, seat and floorboard of a car to bury itself about 2 cm into the road. Estimate its impact velocity (assume each story is 3.0 m - should be larger).

IDS Center by Sharon Mollerus is under a CC BY-SA 2.0 7. A log on a river flows over a waterfall and takes about 4 s to impact the base of the falls. (i) What is the vertical impact velocity of the log? (ii) What is the vertical distance the log fell?
8. A child drops pebbles from a bridge onto a stream 8.5 m below. (i) What is the pebbles' change in displacement? (ii) What amount of time is needed for them to impact the stream?
9. Barrel jumpers such as Annie Edison Taylor experience a drop of around 53 m going over Niagara Falls. (i) For what amount of time would she remain airborne? (ii) What would be her expected impact speed at the base of the falls?

Annie Edson Taylor author unknown Francis J. Petrie photograph collection under the public domain
4.2 Vertical Motion that Changes in Direction
For vertical motion problems that change direction one must sometimes use the symmetrical nature of the trajectory of the vertical motion. It is necessary to look at these questions differently than as a whole event because the displacement equals zero in problems where the object returns to the same height it was launched from. This is similar to the average velocity equaling zero in the hike around the lake in the first example for Chapter 2. These symmetries are shown in the diagram below.
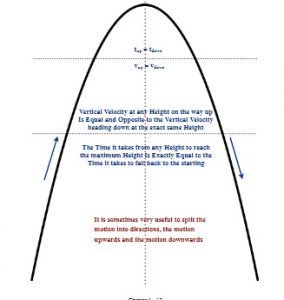
As before, these equations can only be used under constant acceleration situations in the absence of air resistance.
Consider the following examples that solve vertical motion problems where a change in the direction occurs.
EXAMPLE 4.2.1
A water fountain shoots water 8.2 m vertically into the air. (i) What is the impact velocity of the water? (ii) What is the amount of time this water should remain airborne?
Easiest to solve from the top of the trajectory down.
Data
| [latex]\overrightarrow{a} = - 9.8 m/s{^2}[/latex] | [latex]2\overrightarrow{a}\overrightarrow{d} =\overrightarrow{v}_f{^2} -\overrightarrow{v}_f{^2} -\overrightarrow{v}_i{^2}[/latex] |
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]2 (-9.8 m/s{^2}) (-8.2 m) =\overrightarrow{v}_f{^2} - 0 m/s[/latex] |
| [latex]\overrightarrow{v}_f = find[/latex] | [latex]160.7 m{^2}/s{^2} =\overrightarrow{v}_f{^2}[/latex] |
| [latex]\overrightarrow{d}= - 8.2 m[/latex] | [latex]\overrightarrow{v}_f{^2} = 160.7 m{^2}/s{^2}[/latex] |
| t = No | [latex]\overrightarrow{v}_f =\underline{+} 12.7 m/s[/latex] |
| Choose [latex]\overrightarrow{v}_f = - 12.7 m/s (\approx- 13 m/s)[/latex] |
Notice that, for the first problem, the question was solved by looking at only the part of the trajectory from the top of the flightpath to where it impacted and not for the entire trajectory.
Data (ii)
| [latex]\overrightarrow{a}= - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{d} =\overrightarrow{v}_it +½\overrightarrow{a}t{^2}[/latex] |
| [latex]\overrightarrow{v}_i - 0 m/s[/latex] | [latex]- 8.2 m = (0 m/s)(t) + ½ (-9.8 m/s{^2})(t){^2}[/latex] |
| [latex]\overrightarrow{v}_f = No[/latex] | [latex]- 8.2 m = (- 4.9 m/s{^2})(t){^2}[/latex] |
| [latex]\overrightarrow{d}= - 8.2 m[/latex] | [latex](t){^2} = - 8.2 m\div - 4.9 m/s{^2}[/latex] |
| t = find | [latex]t{^2} = 1.67 s{^2}[/latex] |
| [latex]t =\underline{+} 1.3 s (use t = + 1.3 s)[/latex] | |
| Total time in the air is twice this: t = 2.6 s |
EXAMPLE 4.2.2
A rock is thrown straight upwards at 12 m/s from over the edge of a cliff. (i) What is its velocity 1.0 s after launch? (ii) What is its velocity 4.0 s after launch?
Data (i)
| [latex]\overrightarrow{a}= - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{v}_f\overrightarrow{v}_i\overrightarrow{a}t[/latex] |
| [latex]\overrightarrow{v}_i = + 12 m/s[/latex] | [latex]\overrightarrow{v}_f =\overrightarrow{v}_i +\overrightarrow{a}t[/latex] |
| [latex]\overrightarrow{v}_f = find[/latex] | [latex]\overrightarrow{v}_f = + 2.2 m/s[/latex] |
| [latex]\overrightarrow{d} = No[/latex] | |
| t = 1.0 s |
Data (ii)
| [latex]\overrightarrow{a} = - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{v}_f =\overrightarrow{v}_i +\overrightarrow{a}t[/latex] |
| [latex]\overrightarrow{v}_i = + 12 m/s[/latex] | [latex]\overrightarrow{v}_f = + 12 m/s + (- 9.8 m/s{^2}) (4.0 s)[/latex] |
| [latex]\overrightarrow{v}_f = find[/latex] | [latex]\overrightarrow{v}_f = 27.2 m/s (-27 m/s)[/latex] |
| [latex]\overrightarrow{d} = No[/latex] | |
| t = 4.0 s |
EXAMPLE 4.2.3
While watching a baseball game, one particularly long hit remained airborne for about 7.0 s. (i) What must have been its vertical velocity at launch? (ii) What was its maximum vertical displacement?
To solve this problem, the trajectory was broken into two parts: the 3.5 s for the baseball to rise to the top of its trajectory and then the 3.5 s for the baseball to strike the ground after falling from the top of its trajectory.
For the first part, we solved from where the baseball was struck to the top of its trajectory.
Data (i)
| [latex]\overrightarrow{a } = - 9.8 m/s^{2}[/latex] | [latex]\overrightarrow{v}_{f} =\overrightarrow{v}_{i} +\overrightarrow{ a}t[/latex] |
| [latex]\overrightarrow{v}_i = find[/latex] | [latex]0 m/s =\overrightarrow{v}_i + (-9.8 m/s{^2})(3.5 s)[/latex] |
| [latex]\overrightarrow{v}_f = 0 m/s[/latex] | [latex]\overrightarrow{v}_i = 0 m/s + (34.3 m/s)[/latex] |
| [latex]\overrightarrow{d}[/latex] = No | [latex]\overrightarrow{v}_i = 34.3 m/s (\approx34 m/s)[/latex] |
| t = 3.5 s |
For the second part, we solved for the fall back to the ground from the baseball's maximum vertical displacement.
Data (ii)
| [latex]\overrightarrow{a} = - 9.8 m/s{^2}[/latex] | [latex]\overrightarrow{d} =\overrightarrow{v}_it + ½\overrightarrow{a}t[/latex] |
| [latex]\overrightarrow{v}_i = 0 m/s[/latex] | [latex]\overrightarrow{d} = (0 m/s)(3.5 s) + ½ (- 9.8 m/s{^2}(3.5 s){^2}[/latex] |
| [latex]\overrightarrow{v}_f = No[/latex] | [latex]\overrightarrow{d} = (o m) + (-60 m)[/latex] |
| [latex]\overrightarrow{d} = find[/latex] | [latex]\overrightarrow{d} = - 60 m[/latex] |
| t = 3.5 s | This means that the baseball rose 60 m from where it was struck. |
QUESTIONS 4.2 Vertical Motion that Changes in Direction
1. A water fountain shoots water 19.6 m vertically into the air. (i) What is the impact velocity of the water? (ii) What is the amount of time this water should remain airborne?
2. A rock is thrown straight upwards at 5.0 m/s over the edge of a cliff. (i) What is its velocity 0.5 s after launch? (ii) What is its velocity 2.0 s after launch?
3. While watching a golf game, one particularly long shot remained airborne for about 8 s. (i) What must have been its vertical launch component? (ii) How high did it probably go? (maximum vertical displacement)
4. A football is thrown straight upwards with a velocity of 12 m/s. (i) What is its maximum vertical displacement? (ii) What amount of time does it take to impact the ground, if it was thrown upwards when 1.2 m above the ground? (You might have to use the quadratic equation here).

QUESTIONS 4.3 Vertical Motion (These take more time to solve)
1. A base jumper falls for 5.0 s from rest before opening her chute. (i) How fast would one expect her to be traveling? (ii) How far could she fall during the last second? (We are ignoring air resistance in this problem.)
2. Several children are dropping small snowballs from an overpass in attempts to "bomb" oncoming vehicles. If the snowballs need to fall about 5 m before hitting the front grills of cars and the speed of the victim cars are around 80 km/h, by what distance should the children lead the cars? (How close should the cars be before the snowballs are dropped?)
3. A water pipe in the basement is dripping water consistently at about 4 drops each second. If the floor is 2.0 m below the source of the drips, what is the maximum number of water drops that should be in the air at any given time?
REFERENCES

