Chapter 2: Average Speed and Velocity
 This is not the correct picture
This is not the correct picture
2.1 Average Speed & Velocity 3, 4
Speed and velocity are both measures of how quickly something (car, person, jet, etc.) moves from one place to another. While we often run into people using these interchangeably, they are different measures of the same phenomena and require you to look at the same problem in different ways.
Suppose you ask friends to help move a heavy refrigerator roughly 5 m, and the reward will be pizza and beer afterwards. These friends might think this was an excuse to get several of them together but then one important detail is left out. This refrigerator must be moved to an apartment directly above the one it is in. The friends soon understand that the total distance the refrigerator is to be moved is a lot greater than the roughly 5 m. In this instance, the refrigerator is to be moved about 40 m down the hallway, to the stairs where it is lifted up 5 m vertical using stairs to the second floor and then moved 40 m down the hall into the other apartment.
The original friend was not being dishonest about moving the refrigerator 5 m, as it was technically moved 5 m straight upwards. This 5 m straight upwards would be measured as a displacement. The total distance travelled in this example would be 40 m + 40 m + 5 m +, the distance up the flight of stairs.
Measures of distance moved are thus defined as the total distance travelled where the change in displacement is the change in position that includes the direction between these two positions.
These measures are also classified as scalar and vector measures with the scalar just being a number of how much and the vector (it generally has an arrow over the symbol) giving a change in the measure and including the direction involved.
Because of this, you will encounter two sets of measures in introductory physics, a scalar and a vector that can be used to measure the same phenomena. We start this off by looking at the average speed and the average velocity of an event.
[latex]v=\dfrac{\Delta d }{t}[/latex] [latex]\overrightarrow{v}=\dfrac{\Delta \overrightarrow{d} }{t}[/latex]
Where:
[latex]\overrightarrow{v}[/latex] is the Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
[latex]\Delta d[/latex] is the Distance Travelled, commonly measured in Metres (m), Kilometres (km)
[latex]\Delta \overrightarrow{d}[/latex] is the Change in Displacement, commonly measured in Metres (m), Kilometres (km) and includes a direction
[latex]t[/latex] is the Time, commonly measured in second (s) or hours (h)
Often [latex]\textit{speed and velocity}[/latex] involve combining several different motions where one is required to calculate the average speed or velocity of some grouping of linked motions.
[latex]Scalar[/latex] is the amount or how much of a measure and is only a magnitude without other data.
[latex]Vector[/latex] is a measure that also has a direction associated with the measure. It typically refers to magnitude and directional change from the initial to the final measurement. 6
Two of these measures, Time and Distance/Displacement, are classified as base units in the International System of Units7.
[latex]\textit{Time prior to 1900}[/latex], was defined as the fraction 1/86400 of an earth day (24 h x 60 min x 60 s). This was shortly redefined (1956-1967) as the fraction 1/31 556 925.9747 of the tropical year of 1900, January 0 at 12 hours ephemeris time. Time is currently defined (1967) by the energy emitted/absorbed by the caesium-133 atom.
Depending on what fields you study in the future, you will encounter numerous measures of time8, the largest of which is the galactic year, which is the time based on one complete rotation of our galaxy. One galactic year is currently given as 230 million years.
Historically, the measurement of time presented early scientists with a number of challenges. Originally the Egyptian calendar of one year was defined by measurements based on the heliacal rising9 of the binary star Sirius, marking the onset of the flooding of the Nile river. Many ancient civilizations, including the Babylonians, Sumerians, Greeks and Maori, based their calendars on the phenomenon of heliacal rising. The value of heliacal rising allowed the correction of early calendars' lack of a leap year to be corrected. This was replaced with the current Julian (proposed by Julius Caesar in 46 BC) and Alexandrian (based on the early Egyptian calendar) calendars. Currently the Gregorian calendar, a reformation of the Julian calendar, is the one most commonly used.
The hourglass and the water clock10 were early measuring devices of time. The hourglass (sandglass, sand timer, sand clock or egg timer) is recorded in history as far back as 1600s BC in Babylonia and Egypt. These early hourglasses were two joined glass bulbs, one filled with sand that flowed freely from one bulb to the other when the sand-filled bulb was positioned above the other. While common throughout the ancient Middle East, records of its arrival in Europe indicate its presence there from the mid-1300s. The hourglass remained in common use but started to decline in popularity as a timing device in the 1500s, due to the technological development of mechanical clocks.

Water clocks are claimed to have been present in China as early as 4000 BC, and documented in Egypt around the 1600s BC. The design of a water clock is simple; water flows slowly from an upper source to a container where the amount of water, and hence time, can be measured. Hourglasses and water clocks depended on the rate of flow of either sand or water, which indicated the passage of time.
The image to the left is of the oldest surviving water clock from Egypt, 1400 BC. The image below is of water clock calculations by Nabû-apla-iddina (600-500 BC).
Could use water clock image


Galileo Galilei created a time-measuring device called the pulsilogon, which he based on the regularity in the time of a swinging pendulum. One of his first applications of the pulsilogon was to measure a person's pulse. This was accomplished by lengthening or shorting the pendulum until the time for one swing of the pendulum (called the period) matched the rate of the pulse of the person. Medical historians view this invention as the birth of precision in medicine. Using this pendulum time piece, Galileo was able to discover some of his foundational concepts in physics11.
Length prior to 1793 was defined by the fraction 1/10 000 000 of the meridian length (through Paris) between the North Pole and the Equator. This also was redefined for a short time (1960-1983) by the wavelength of radiation emitted by the Krypton-86 atom. Length is currently defined (1983) by a Speed Equation: the distance that light travels in a vacuum in a fraction of 1/299 792 458 seconds.
Using the speed equation: [latex]v =\dfrac{d}{t}[/latex], we can see that [latex]d =\textit{ v t}[/latex] which means for the base measure of length:
One meter (m) = (speed of light) (1/299 792 458 seconds).
Historically, the measurement of length originates from multiple cultures and civilizations. Common English measures such as the inch (length of a thumb), the foot (the length of a foot), the yard (length of an average pace) and the mile (one thousand of the Roman two steps to a pace) all have historical origins. Most common of all these measures for length was the cubit, which was measured as the distance between the elbow to the tip of the middle finger. As you can remember from Chapter One, there are many measures used for length, each having specific uses for various trades and specialties.
To get around the confusion of different measures of length and other measures, the metric system of measures was created during the French Revolution in 1799. The early metric system, based on a decimal fraction of the distance from the Equator to the North Pole, was also used to define the kilogram, i.e., the mass of water contained in a cube of 10 cm in length (decimetre). As time passed, the need for greater accuracy defined the metre and kilogram from two standard artifacts created out of platinum and iridium. These constructions were used to define length and mass, having since becoming common measures in all countries except the United States, Myanmar (Burma) and Liberia. The image to the right is the only surviving artifact of the original metre, and is located at 36, rue Vaugirard, France.

The following example will help to explain the difference in measuring speed and velocity.
EXAMPLE 2.1.1
Using the following sketch of a hike around a lake, solve for the following questions.
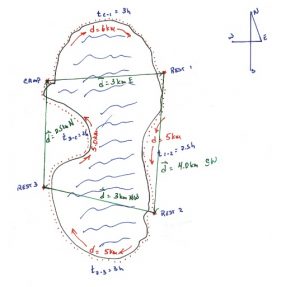
(i) What is the average speed and velocity in walking from the camp to the 1st rest spot?
Data:
| [latex]v = find[/latex] | [latex]v=\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v}= find[/latex] | [latex]\overrightarrow{v}=\dfrac{\overrightarrow{d}}{t}[/latex] |
| [latex]\Delta{d} = 6 km[/latex] | [latex]v =\dfrac{6\textit{km}}{3h}[/latex] | [latex]\overrightarrow\Delta{d} = 3 km E[/latex] | [latex]\overrightarrow{v} = \dfrac{3 km E}{3h}[/latex] |
| [latex]t = 3 h[/latex] | [latex]v = 2\dfrac{km}{h}[/latex] | [latex]t = 3 h[/latex] | [latex]\overrightarrow{v}=\dfrac{1 km}{h e}[/latex] |
(ii) What is the average speed and velocity in walking from the 1st to the 2nd rest spot?
Data:
| [latex]v= Find[/latex] | [latex]v=\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v} = find[/latex] | [latex]\overrightarrow{v} =\overrightarrow{\dfrac{d}{t}}[/latex] |
| [latex]\Delta{d} = 5[/latex] | [latex]v =\dfrac{5 km}{2.5 h}[/latex] | [latex]\Delta{d}= 4.0\textit{km SW}[/latex] | [latex]\rightarrow=\dfrac{4.0\textit{km SW}}{2.5 h}[/latex] |
| [latex]\Delta{d}= 5[/latex] | [latex]v=\dfrac{5 km}{2.5 h}[/latex] | [latex]\Delta{\overrightarrow{d}}= 4.0\textit{km SW}[/latex] | [latex]\overrightarrow{v}=\dfrac{4.0\textit{km SW}}{2.5 h}[/latex] |
| [latex]\Delta\overrightarrow{d}= 5[/latex] | [latex]v=\dfrac{5 km}{2.5 h}[/latex] | [latex]\Delta{d}=4.0\textit{km SW}[/latex] | [latex]\overrightarrow{v}=\dfrac{4.0\textit{km SW}}{2.5 h}[/latex] |
| [latex]t=2.5 h[/latex] | [latex]v=\dfrac{2 km}{h}[/latex] | [latex]t=2.5 h[/latex] | [latex]\overrightarrow{v}=1.6\dfrac{km}{\textit{h SW}}[/latex] |
(iii) What is the average speed and velocity in walking from the 2nd to the 3rd rest spot?
Data:
| [latex]v = find[/latex] | [latex]v =\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v} = find[/latex] | [latex]\overrightarrow{v}=\dfrac{\overrightarrow{d}}{t}[/latex] |
| [latex]\Delta{\overrightarrow{d}}= 5 km[/latex] | [latex]v =\dfrac{5 km}{3 h}[/latex] | [latex]\Delta{\overrightarrow{d}}=3.0\textit{km NW}[/latex] | [latex]\overrightarrow{v}=\dfrac{3\textit{km NW}}{3h}[/latex] |
| [latex]t = 3 h[/latex] | [latex]v = 1.67\dfrac{km}{h}[/latex] | [latex]t = 3 h[/latex] | [latex]\overrightarrow{v}= 1\dfrac{km}{\textit{h NW}}[/latex] |
iv) What is the average speed and velocity in walking from the 3rd rest spot back to the camp?
Data:
| [latex]v = find[/latex] | [latex]v=\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v}= find[/latex] | [latex]\overrightarrow{v}\dfrac{\overrightarrow{d}}{t}[/latex] |
| [latex]\Delta{d}= 5 km[/latex] | [latex]v =\dfrac{5 km}{2 h}[/latex] | [latex]\Delta{\overrightarrow{d}} = 2.5 km N[/latex] | [latex]\overrightarrow{v} = \dfrac{2.5 km N}{2 h}[/latex] |
| [latex]\Delta{d}= 5 km[/latex] | [latex]v = 2.55 km[/latex] | [latex]t = 2h[/latex] | [latex]\Delta{d} = 1.25\textit{h N}[/latex] |
Data:
(v) What is the average speed and velocity walking the entire hike? (Do not include the time taken to rest.)
| [latex]v = find[/latex] | [latex]v=\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v}= find[/latex] | [latex]\overrightarrow{v}\dfrac{\overrightarrow{d}}{t}[/latex] |
| [latex]\Delta{d}= 21 km[/latex] | [latex]v = \dfrac{21 km}{10.5 h}[/latex] | [latex]\Delta{\overrightarrow{d}}= 0 km[/latex] | [latex]\overrightarrow{v} =\dfrac{0 km}{10.5 h}[/latex] |
| [latex]t = 10.5 h[/latex] | [latex]v =\dfrac{2 km}{h}[/latex] | [latex]t = 10.5 h[/latex] | [latex]\overrightarrow{v} =\dfrac{0 km}{h}[/latex] |
Notes:
∆d = 6 km + 5 km + 5 km + 5 km
∆d = 21 km
t = 3 h + 2.5 h + 3 h + 2 h
t = 10.5 h
Final change in displacement = 0 km. The hikers ended up in the same position that they started from.
EXAMPLE 2.1.2
What is the average speed and velocity of a hiker who walks 15 km (displacement change of 3.0 km NE) in 5.0 h?
Data:
| [latex]v = find[/latex] | [latex]v=\dfrac{d}{t}[/latex] | [latex]\overrightarrow{v}= find[/latex] | [latex]\overrightarrow{v}\dfrac{\overrightarrow{d}}{t}[/latex] |
| [latex]\Delta{d} = 15 km[/latex] | [latex]v =\dfrac{15 km}{5 h}[/latex] | [latex]\Delta{\overrightarrow{d}} = 3.0 km NE[/latex] | [latex]\overrightarrow{v} =\dfrac{3.0 km NE}{5h}[/latex] |
| [latex]t = 5.0 h[/latex] | [latex]v = \dfrac{3.0 km}{h}[/latex] | [latex]t = 5.0 h[/latex] | [latex]\overrightarrow{v}=\dfrac{0.60 km}{h NE}[/latex] |
EXAMPLE 2.1.3
What is the possible area covered by a person who walks 100 m in an unknown direction?
Solution:
This question is different than the two previous examples as it does not require a speed or velocity calculation. It is a geometry question, specifically, the area of a circle of radius 100 m.
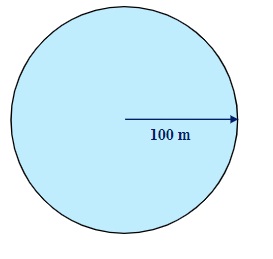
A = π r2
A = π (100 m)2
A = 10 000 π m2
or A = 31 400 m2 (three digits accuracy)
QUESTIONS: 2.1 Average Speed and Velocity
- What must your average speed be to travel 684 km in 9.0 h?
- When Donovan Bailey ran the 100 m in 9.84 s, what was his average speed?
- A Cruise Ship moves at an average speed of 25 km/h. (i) What distance does it travel in a day? (ii) What amount of time does it need to travel 800 km?
- A person walks around a store traveling 65 m in 155 s but only changes their displacement by 18 m NW. What is the person's average speed and velocity?
- You are given a task to find a puppy who wandered 60 m from your back yard in an afternoon. What size of search area would you need to check?

2.2 Average Speed/Velocity (Converting Units)
To be able to solve a problem in real life, one will often be required to convert from multiple units to a shared common unit. For speed, you can be given speeds in m/s, cm/s, km/h, km/s, length in m, cm, km, light years, and time in seconds, minutes, hours, days or years. You should make sure that all units are the same measure before you start solving the problem. Solving problems is significantly easier if all units are converted to the same type of measure.
EXAMPLE 2.2.1
What must your average speed be in km/h, to travel 10.4 km in 90 minutes?
You can see that we have two different measures in this question, distance travelled in km and time measured in minutes, with the final answer to be in km/h. Therefore the time must be converted to hours.
v = find First: 90 minutes is divided by 60 minutes to convert to hours
∆d = 10.4 km Therefore 90 minutes = 1.5 hours
t = 90 minutes or 1.5 h
[latex]Now\colon=v\dfrac{d}{t}[/latex]
[latex]v =\dfrac{10.4 km}{1.5 h}[/latex]
[latex]v\approx6.9 km/h[/latex]
EXAMPLE 2.2.2
If a distracted driver traveling at 60 km/h looks at their cell phone for 9.0 s, how far have they driven without looking at the road?
You have a choice to convert the time to hours or the speed to m/s. Easier to convert the speed. Best to remember this conversion Factor: 1 m/s = 3.6 km/h.
[latex]v =\text{ 60 km/h or 16.7 m/s}[/latex] [latex]Now\colon\dfrac{v}{d}\text{or d = v t}[/latex]
Δd = find [latex]d = (16.7 m/s) (9.0 s)[/latex]
[latex]t = 9.0 s[/latex] [latex]d = 150[/latex]
EXAMPLE 2.2.3
What distance is covered by a person who drives an average speed of 50 km/h in the city for 40 minutes, and then drives at an average speed of 110 km/h for 1 hour and 20 minutes?
Data:
v = 50 km/h First convert 40 minutes to hours ... (divide by 60 minutes = 1 hour)
∆d = find 40 minutes ÷ 60 = 2/3 h
t = 40 minutes [latex]Now: v =\dfrac{d}{t}[/latex] or d = v t
d = (50 km/h) (2/3 h)
d = 33.3 km
Data:
v = 110 km/h
∆d = find
t = 1 hour 20 minutes
Need to convert 1 hour 20 minutes to hours
1 hour 20 minutes = 1 1/3 h or 4/3 h
[latex]Now: v =\dfrac{d}{t}[/latex] or d = v t
d = (110 km/h) (4/3 h)
d = 146.7 km
Therefore the total distance traveled is:
dtotal = 33.3 km + 146.7 km
dtotal = 180 km
QUESTIONS 2.2 Average Speed/Velocity (Converting Units)
- Show the conversion factor between metres/second and kilometres/hour.
- If you are driving 90 km/h and look to the side for 3.0 s, how far would you travel in this inattentive period?
- What distance will an auto travel in 55 minutes while traveling at 110 km/h?
- A killer tomato can travel at 24 km/h. What distance could it travel in 1 hour & 15 minutes?

https://www.flickr.com/photos/tohoscope/3976192672 Attack of the Killer Tomatoes by Toho Scope is under CC BY-SA 2.0. - A model aircraft can fly at 30 m/s. If it breaks free from radio control, what distance could it fly, if it has enough fuel for 2 hours & 20 minutes of flight?
- Two transport aircraft take off at the same time, headed on the same flight path. One travels at 240 km/h for 3 hours 40 minutes before it lands, and the other travels at 90 m/s for 2 hours 55 minutes before it lands. How far apart are the planes after they have landed?
Article to read - Half of Parents in America Use Cellphones With Young Children in the Car.
http://www.newsweek.com/half-parents-america-use-cell-phones-young-children-car-1020133?
2.3 Relative Velocity in Two Dimensions 12, 13 [should these be footnotes?]
In real life, you often encounter motion on, in or on top of some moving medium. Common examples of this are one walking on an escalator, a boat moving on a stream or a river, or an aircraft that is flying into moving air, such as the jet stream.
The simplest way to understand this is to relate to a common experience that most of us have had: walking in or opposite to the direction that an escalator is moving.
When walking in the same direction as the escalator is moving, you travel faster and only need to add the speed of the escalator to how fast you are walking to calculate your relative speed. An equation for this looks like:
vrelative = vescalator + vwalking
When walking in the opposite direction to the one in which the escalator is moving, you travel more slowly and can simply subtract the speed of the escalator from the speed you are walking to calculate your resulting speed. An equation for this looks like:
vrelative = vescalator + vwalking
Should you not walk fast enough, you could easily end up moving backwards, even though you are walking forwards.
This is slightly more complicated for aircraft and watercraft that are moving in air or water that itself is moving. If moving in the same direction or the opposite direction that the air or water is moving, one generally adds or subtracts these two velocities as we did above for walking on an escalator. If moving at an angle to the direction the air or water is moving, then generally you draw a sketch and use trigonometry to find the relative velocity.
This is done using either right angle trigonometry and the Pythagorean Theorem or by using non-right angle trigonometry. The equations to use for these are:
For any right triangle a, b and c:
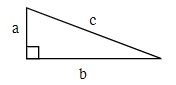
a2 + b2 = c2
For any non-right triangle a, b and c:
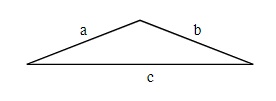
a2 = b2 + c2 - 2bc cos A
b2 = a2 + c2 - 2ac cos B
c2 = a2 + b2 - 2ab cos C
Where:
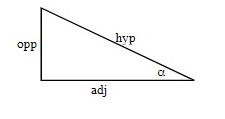
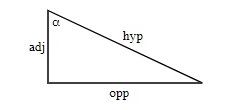
Basic Trigonometric Ratios
[latex]Sin =\dfrac{Opposite}{Hypotenuse}[/latex] [latex]Cos =\dfrac{Adjacent}{Hypotenuse}[/latex] [latex]Tan =\dfrac{Opposite}{Adjacent}[/latex]
Trigonometric Defined Sides

It is challenging to find any person that is not told at an early age that the Earth orbits around the Sun. However, if we go back around four centuries, one of the greatest scientists of his time, Galileo Galilei (1564-1642), was threatened with torture and nearly executed for teaching this doctrine. Galileo’s position had been held before by a number of Greek philosophers, including Eratosthenes (276-194 BC) and Aristarchus (310-230 BC), who had reasonably accurate measures of the size of the Earth and Moon and had calculated the distances from the Earth to the Moon and the Sun. All of this was accomplished by using a combination of astronomy and geometry. Despite these advances, Ptolemy (100-170 AD) created an elaborate model of the universe using what he described as crystalline spheres, on which all known heavenly bodies moved.
The Ptolemaic system of understanding the motions of the universe survived for the next fourteen centuries until Nicolaus Copernicus (1473-1543) challenged this model in 1530 by placing the Sun in the center of the solar system, orbited by the planets (heliocentric). The arguments against a heliocentric model mainly stemmed from a blend of Christian beliefs and a failure to understand relative motion. People believed that the stresses of a rotating Earth would cause it to tear apart, flying in different directions, and that any object tossed up into the air would land quite far away, opposite to the direction of the Earth's spin.

The reigning thought was that man was God’s greatest creation and therefore must be at the center of the universe. Copernicus raised concerns over the Aristotelian concept of why only the Earth would be comprised of the elements of earth, water, air and fire, yet all objects in the heavens were composed of the quintessence.
One of Copernicus’s supporters, the Dominican friar Giordano Bruno (1548-1600), expanded the Copernican model to declare that stars were spread throughout infinite space and there existed the possibility of other inhabited worlds. Giordano Bruno was burned to death at the stake in 160014 for holding such beliefs. While Bruno paid with his life for his belief in the accuracy of the heliocentric model, Galileo Galilei’s technological advancement, the telescope, established that the Moon was quite similar to the Earth, and that if this was true the known planets were also like Earth and not composed of the quintessence.
While Galileo was a gifted and curious scientist, he found himself with financial burdens15 that at the time outstripped his salary from the University of Padua. His understanding and refinement of the telescope, turning it from 3x magnification to over 9x magnification, won him immediate praise and financial reward from military leaders at the time. This advancement gave the military defenders of Venice16 an extra two or more hours' warning of advancing ships before people on the ships could see the city. Galileo was granted tenure at the university for this advancement, with an increased salary.
Some of Galileo’s first discoveries with his improved telescope included mountains on the Moon and, on January 7, 1610, four moons on the planet Jupiter17. Understanding the risks of his discovery, Galileo name the moons of Jupiter after members of the Medici family, Dukes of Tuscany, gifting the Duke with a further improved 20x magnification telescope to better be able to see the moons named after his family members.
Despite this action, Galileo was warned not to venture outside the protection of the city-state of Venice, which wanted to tax the Church, whose interpretation of scripture defined Man as the centre of a universe that orbited the Earth (geocentric). In 1616, the Catholic Church condemned the Copernican system (Protestant churches of the time allowed for the freedom to interpret the Bible) and Galileo’s stance on the heliocentric universe now placed Galileo in danger of heresy. Galileo increased this risk by not only continuing to defend his position but writing of his beliefs in a work called a “Dialogue Concerning the Two Chief Systems of the World-Ptolemaic and Copernican.” So confident was he in the validity of his work, Galileo created characters in his book, including one named Simplicio, who clearly represented the current Pope, who discussed the merits of his position.
Galileo’s book was published in March 1632. Five months later, the order to cease publishing was accompanied by an order for Galileo to stand trial. In 161618, when Galileo was threatened with torture in the dungeons below the Vatican, he was given a tour of these torture chambers. He agreed to tone down the writings in his Dialogues, and spent his remaining years in penance under house arrest at his villa until his death in 164219. Perhaps what is unusual about Galileo’s sentence is that the Vatican ordered it to be widely published in scientific circles. A number of historians have argued that the strong stance taken by the Catholic church at the time effectively discouraged the development of science in Italy for many generations afterwards.
Galileo’s Two New Sciences
The Discourses and Mathematical Demonstrations Relating to Two New Sciences, Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze (1638), was Galileo’s final book, written while he was under house arrest. Following the publication of his Dialogue Concerning the Two Chief Systems of the World-Ptolemaic and Copernican, the Vatican banned any further publication of any of Galileo’s works, including what he would potentially write in the future. This ban resulted in failed attempts to publish his last work in France, Poland and Germany, but it was published by Lodewijk Elzevir in Holland. Galileo seems to have escaped paying a price for this new crime, since all 50 of the Two New Sciences books imported into Rome quickly sold.
While Two New Sciences was written in a similar form to his earlier work, Two Chief Systems, the discussions between the familiar Simplicio, Sagredo and Salviati, Simplicio no longer held the simplistic, stubborn Aristotelian beliefs of the time, and instead represented Galileo’s early beliefs as he started the studies. Sagredo represented Galileo’s changing views and Salviati represented Galileo’s final views on his research. Such a change in his writing could also have influenced Galileo's escaping any further punishment outside of house arrest. The importance of this work and Galileo’s trials expose the conditions and the world in which these early researchers worked, and Galileo’s work to understand relative motion.
Galileo explained why an object on Earth falls straight even though the Earth spins, through his theory regarding objects on a moving ship. Aristotelian arguments against the rotation or spin of the Earth suggested that an object dropped at the equator would land far behind the position from which it was dropped. For instance, if the Earth is rotating at 1000 km/h or 278 m/s at the equator and a dropped object takes two seconds to reach the ground, the object would land 556 m behind; an object taking 4 s to reach the ground would fall behind over a kilometre.
Galileo compared what was expected to happen according to Aristotelian logic to what can actually be observed in an object dropped on a moving ship. Even without conducting the actual experiment, anyone working on ships knew that objects fall straight down20. Galileo also proposed that an observer from shore would see a projectile type motion. In this example, Galileo explained that objects in motion on moving surfaces would be observed differently by an observer on the moving surface and one standing on a surface that is stationary.
The following examples explore the algebra of relative motion.
EXAMPLE 2.3.1
What is the average speed of an airliner that has an air speed of 750 km/h flying directly into a jet-stream of 115 km/h?

The solution of this question is to subtract the speeds. They are in opposite directions:
v = 750 km/h - 115 km/h
v = 635 km/
EXAMPLE 2.3.2
What is the average speed of an airliner that has an air speed of 750 km/h flying in the same direction as a jet-stream of 115 km/h?
The solution of this question is to add the speeds. They are in the same directions:
![]()
v = 750 km/h + 115 km/h
v = 865 km/h
EXAMPLE 2.3.3
What is the average velocity of an airliner that has an air speed of 750 km/h East flying in a jet-stream of 115 km/h South? Can you calculate the angle it is traveling at?

The solution for this question requires you to use the Pythagorean Theorem:
v2 = (750 km/h)2 + (115 km/h)2
v2 = 562500 km2 /h2 + 13225 km2 /h2
v2 = 575725 km2 /h2
Taking the square root of both sides gives us the speed:
v = 758.8 km/h or 759 km/h (sig correct)
Using the Tangent Function the angle is 8.7
QUESTION 2.3 Relate Velocity in One Dimension
- A Boeing 747-400 whose cruising speed is 918 km/h (mach 0.855) travels a distance of 1995 km in 2.5 h. What was the average speed of the headwind slowing this jet?
- An airplane travels 1600 km at a speed of 1000 km/h. It then runs into a headwind that slows it to 875 km/h for the next 2100 km. What was the average speed of the plane for this trip?
- One of the problems you encounter in real life is to swim or row across a river. In these cases the swimmer or rower swims at an angle across the river to maintain a straight path. This problem will look at the simplest form of this question, of swimming straight across the river and ending up drifting down from the starting point on the other side.
In this problem, consider a swimmer that can swim at 1.0 m/s and who sets off to swim 220 m across river which is flowing at 3.2 m/s. How far down river, will this swimmer have drifted by the time they have reached the other side?


4. The Hindenburg class airships were 245 m long, 41 m wide (longer than 3 Boeing 747s parked end-to-end and only 24 m shorter than the Titanic). During their short commercial lifespan, the Hindenburg travelled 308, 323 km between Frankfurt, Rio De Janeiro and New York carrying a total of 2,798 passengers and 145 tonnes of freight and mail. Given that the maximum speed of the Hindenburg was 135 km/h, the speed of any wind it was flying into made for a significant impact on its travel.
Consider the following:
(i) What is the average speed of the Hindenburg airship that has an air speed of 135 km/h flying directly into a jet-stream of 45 km/h?
![]()
(ii) What is the average velocity of a Hindenburg airship that has an air speed of 135 km/h flying in the same direction as a jet-stream of 45 km/h?
![]()
(iii) What is the average velocity of an Hindenburg airship that has an air speed of 135 km/h East-flying in a jet-stream of 45 km/h South? Can you calculate the angle it is traveling at?

(iv) Suppose the Hindenburg needs to fly in a straight line for 250 km while encountering a 900 crosswind of 42 km/h. At what angle must it fly at to counteract the wind that is actively blowing it off course?

(v) What would its net ground speed towards its intended destination?
(vi) How much time would this take for this journey?
5. The following shows a jet-stream forecast for Saturday 11th, 2014 that focuses on the Continental United States.
? PICTURE - I CANNOT FIND
(i) What is length of the dashed line from X to X _____________?
(ii) Using a scale of 1 cm = 285 km, what distance does this represent? _____________
(iii) What is the expected speed of the jet-stream along this dashed line in km/h? ____________
(iv) If a Boeing 747-100B cruises at 893 km/h, how much time would it take to go from the Saskatchewan border to its destination just above Texas? _____________
(v) For the return trip to Saskatchewan? _____________
Article to Read - https://onezero.medium.com/planes-are-ruining-the-planet-new-mighty-airships-wont-d8eb39418acc
Article to Read -https://en.wikipedia.org/wiki/Jet_stream
Article to Read - Flight from L.A. to London reaches 801 mph as a furious jet stream packs record-breaking speeds: https://www.latimes.com/science/la-sci-sn-jet-stream-flight-20190219-story.html?fbclid=IwAR0aVR2x4ef0M_djRV6LcElE5hdUcXmYkNCPvHTBkjGprc-ebqCHBjb37kEOn
March 15, 2019 Jet Stream speed reached 386 km/h due to disruptive climate conditions over North America.
QUESTIONS 2.4 Average Speed and Velocity ... These take more time to solve
Best to grab a coffee to do these following questions. They are meant to make you think.
- In a simulation of a search and rescue, a person is assumed to walk at 4 km/h, in an unknown direction. How big is the search area one would need to cover after this person has been walking for 8 h? (You need to use the area of a circle for this problem.)
- A passenger train travels at 80 km/h for 1/2 hour, and then after leaving city limits, 100 km/h for 2 hours. (i) How far did it travel? (ii) What was its average speed for this trip?
- A rally car driver drives the first 100 kilometres of a 200 kilometre race at an average speed of 30 km/h. What must be the average speed of this driver on the return trip to have an overall average speed for the entire race of 60 km/h?
- What amount of time does it take an echo to return to a person standing 100 m away from a cliff? (Use a speed of sound of 350 m/s).
- A brother and sister both start from home at the same time and drive to work 40 km away. The posted speed for the road they travel is 110 km/h. If the sister speeds by 10 km/h and the brother travels 10 km/h under the speed limit, by what difference in time will they arrive at work?
- A person's left and right palms are moving toward each other at a speed of 4.0 m/s each. A fast-flying insect originally on the left palm flies to the right palm at 10 m/s; when it arrives there it immediately turns back to the left palm flying at the same speed. It continues to fly back and forth between the palms (originally separated by 1.0 m) until the end. What is the total distance travelled by the insect?
QUESTIONS 2.5.1 Horse Transportation
The people of the USA traveled around 8.8 x 1012 km in the year 2005. If only horses were used for transportation, then:
(i) How many horses would the USA need to provide transportation for its citizens? A horse can travel on average 32 km in 1 day.
(ii) If the average horse needs 0.8 hectares of land to graze on for the year, then how many hectares would be needed to feed the horses required by the USA?
QUESTIONS 2.5.2 The First Measure of the Speed of Light...
...was a failure. Galileo recorded an experiment in which he positioned himself on one hilltop with an assistant on a different hilltop. The premise was that when Galileo opened the shutter of his lantern, the assistant would open the shutter of their lantern when they saw the light from Galileo's lantern. Galileo would then measure the time it took and, knowing the distance separating the two hilltops, he would be able to measure the speed of light. Looking back at Galileo's experiment, if we assume a half second reaction time for the assistant to open their lantern shutter, light would travel 150 000 km, which is a distance of 3.75 times around the Earth, in that half second. Galileo's experiment hand no chance of success. If Galileo could have had an assistant on the Moon, light would take 2.56 s to travel back and forth between the Earth and Moon, and even then we would need to add in the reaction time it takes to open the lantern shutter.
The breakthrough to measuring the speed of light came from observing the moon orbiting Jupiter. While Galileo's experiment failed, his suggestion that the orbital period of the four largest Moons of Jupiter could be used as a kind of celestial clock was the key to being able to measure the speed of light. Discovered by Galileo in 1610, Jupiter's satellite Io takes only 1.759 days to orbit the planet. In xxxx Ole Romer (1644-1710) recorded details of the orbit of Io, and noticed an error in his measurements. As the Earth orbited the Sun, moving farther from and closer to the planet Jupiter, the measured period of Io in orbit around Jupiter varied by some 22 minutes. The traveling time of Io was 22 minutes late when the Earth was farthest away from Jupiter, compared to when the Earth was at its closest point to Jupiter. Romer interpreted this to mean that took 22 minutes for light to travel across the Earth's orbit.
Questions:
(i) Given that the radius of the Earth's orbit averages 1.49 x 1011 m, calculate the speed of light using Romer's value of 22 minutes. Christian Huyens (1629-1695) was the first to do this calculation.
(ii) Later on, Romer's measure of 22 minutes was found to be incorrect, and was corrected to 16.7 minutes. What would be the corrected measure of the speed of light using this data?

QUESTIONS 2.5.3 The Time Delay in Communication Between Earth and Mars
CAN'T FIND PICTURES... NOT SURE OF JUST COPY OVER
The challenges concerning the exploration of Mars from Earth and in placing humans on the Martian surface is the amount of time it takes for light or any other communication signal to travel between the two planets. The above sketch shows Mars and Earth in orbit around the sun, where while the Earth has nearly a circular orbit, and Mars has more of an elliptical orbit. You will also notice that the units in this sketch are given as A.U. (Astronomical Units), where 1 A.U. is defined as the average distance between the Earth and the Sun in its orbit.31
1 A.U. = 149 597 870 700 m
Since the distances between the Earth, Mars and the Sun in the above sketch are shown in A.U. we will need to convert all A.U. distances to metres (m).
One other factor that needs to be defined in working to solve the communication is the speed of light (c) which is the speed at which signals travel. All transmissions, including communication radio, television, radar, x-rays, gamma rays, infrared, ultraviolet radiation and light, travel at the same speed and are all part of the same family called electromagnetic radiation (EM). The speed of light can be affected by the medium or object through which the Em is traveling, but its maximum is in open space that is not affected by gravity. This speed, indicated by the symbol c, is of great significance in the study of physics.
c = 299 792 458 m/s
Using the above data, find the minimum amount of time it takes to send and receive a message sent from either planet for the following orbital separations between Mars and the Earth:
(i) d = 0.38 A.U. (Martian Perihelion)
(ii)d = 0.66 A.U. (Martian Aphelion)
iii) d = 2.66 A.U. (Maximum possible separation between the Earth and Mars)
Astronomical Unit: https://en.wikipedia.org/wiki/Astronomical_unit
QUESTIONS 2.5.4 The Carrington Event
One of the challenges or dangers to Earth-based technological devices is interference from an intentional Electromagnetic Pulse or from the natural phenomenon of a Solar Flare. Solar flares are powerful “Coronal Mass Ejections” (CMEs) composed of trillions of kilograms of charged electric particles traveling up to several million kilometres per hour from the Sun through space. These solar flares are massive in size, compared to the Earth, and while they are not expected to cause any harm to life on Earth, they have the potential to destroy technological devices. Because of this threat, it is becoming increasing relevant to have advance warning of such storms that are directed towards the Earth. The largest recorded Solar Storm in history dates back to August 28, 1859 and has been named the Carrington Event (now identified as SOL 1859-09-01) after Richard C. Carrington (1826-1875), who observed and recorded the CME. The effect of this coronal storm was so great that in some places on Earth people could read newspapers at night due to the brightness of the Northern Lights, and telegraph operators around the world reported being shocked or electrocuted by devices hooked up to the wires used for communication. In 2012, a CME similar in strength to the Carrington Event missed the Earth by nine days. Question: What was the speed of the CME ejected in the Carrington Event, if it took an estimated 17.6 hours to travel the distance between the Earth and the Sun? (d = 1.5 x 1011 m)
Article to Read - NASA Developing Early Warning System for Solar Flares: https://interferencetechnology.com/nasa-developing-early-warning-system-for-solar-flares/
Article to Read - Byrd, D. (2012-12-09) Are Solar Storms dangerous to us?: https://earthsky.org/space/are-solar-storms-dangerous-to-us
Research Article - Lloyds (2013) Solar Storm risk to the North American Electric Grid: Solar Storm Risk to the North American Electric Gridhttps://www.lloyds.com/.../lloyds/...risk.../solar-storm-risk-to-the-north-american-elect...

REFERENCES:
1. Mechanical Universe - Episode 5 - Vectors: https://www.youtube.com/watch?v=MWrOozSSdW8
2. Image is from “How fast could you travel across the U.S. in the 1800s?” Source: https://www.mnn.com/green-tech/transportation/stories/how-fast-could-you-travel-across-the-us-in-the-1800s
3. Extra Help - Distance and Displacement: https://www.physicsclassroom.com/class/1DKin/Lesson-1/Distance-and-DisplacementExtra Help - Speed and Velocity: https://www.physicsclassroom.com/class/1DKin/Lesson-1/Speed-and-Velocity
4. Galileo is credited as being the first to measure speed as the ratio of distance travelled to the time taken.
5. Average speeds and velocities are generally different than the speed and velocity at some instant.
6. Extra Help - Scalars and Vectors: https://www.physicsclassroom.com/class/1DKin/Lesson-1/Scalars-and-Vectors
7. The other fundamental measures are:• Kilogram (kg) is the base measure used in quantifying mass• Ampere (A) is the base measure used in quantifying electric current• Kelvin (K) is the base measure for quantifying temperature• Mole (mol) is the base measure used in quantifying the number of atoms in a substance • Candela (cd) is the base measure used in quantifying the luminous intensity of any light source
8. https://en.wikipedia.org/wiki/Unit_of_time
9. Heliacal rising refers to the moment that a star becomes briefly visible on the Eastern horizon at dawn, having not been visible during the previous year.
10. The sundial while known at the same time as these two clocks is not covered in this Chapter.
11. Article to Read - Big Bang may have created a Mirror Universe where time runs backwards: https://www.pbs.org/wgbh/nova/article/big-bang-may-created-mirror-universe-time-runs-backwards/?fbclid=IwAR1iKXC6uzGJIHEjIwcItxu2q155_FmjqvmqPi9kJ1rEM0i9MMJ431ueuLs
12. Extra Help - Relative Velocity and Riverboat Problems: https://www.physicsclassroom.com/class/vectors/Lesson-1/Relative-Velocity-and-Riverboat-Problems
13. Galileo is credited with developing the concept of relative velocity in his early experiments that he designed to prove the Earth was a sphere and that it rotated around the Sun. It was his publishing of this in his work “Dialogues Concerning the Two Chief World Systems”. Source: http://www.physicscentral.com/explore/plus/galilean-relativity.cfm
14. Article to Read - Was Giordano Bruno Burned at the Stake for Believing in Exoplanets?: https://blogs.scientificamerican.com/observations/was-giordano-bruno-burned-at-the-stake-for-believing-in-exoplanets/
15. Galileo was the oldest son in his family and found himself responsible to raise the dowries of his younger sisters and of the financial care of three children by his mistress, Marina Gamba.
16. Venice at the time of Galileo was rather a boisterous city with a population of around 150,000 people consuming in excess of 40 million bottles of wine each year.
17. These two discoveries acted to destroy the concept of heavenly bodies made of the quintessence. Galileo’s later discovery that the Sun had spots on it further tarnished the image of the perfection of the quintessence.
18. In 1616 the Catholic church banned the 1543 book by Nicholas Copernicus “On the Revolutions of the Celestial Spheres,” which contained the theory that the Earth revolved around the sun.
19. It is worth noting that it was understood that Galileo’s punishment reflected his behavior to wards authority and not of his scientific achievements. As written by a Jesuit scholar of his time: “If Galileo had only known how to retain the favor of the fathers of this college, he would have stood in renown before the world; he would have been spared all his misfortunes, and could have written about everything, even about the motion of the earth.” What should be noted is the the Jesuits were soon teaching that the Earth orbited the Sun as in a heliocentric model in China and other parts of the world.

