Chapter 13: Friction and Accelerated Motion
 NOT SURE if this picture is copyrighted. I could not find it out on the web so just made it a jpeg.
NOT SURE if this picture is copyrighted. I could not find it out on the web so just made it a jpeg.
Equations Introduced and Used for this Topic:
| [latex]a=\dfrac{\Delta{v}}{t}[/latex] | [latex]\overrightarrow{a}=\dfrac{\Delta{\overrightarrow{v}}}{t}[/latex] |
| [latex]\Delta{v} = v_{f} - v_{i}[/latex] | [latex]v=\dfrac{(v_{i} + v_{f})}{2}[/latex] |
| [latex]v_{f} = v_{i} + at[/latex] | [latex]2ad = v_{f}^{2} - v_{i}^{2}[/latex] |
| [latex]d = v_{i}t + ½ at^{2}[/latex] | [latex]d =\dfrac{(v_{i}+ v_{f}) t}{2}[/latex] |
Ff = µN or µmg (simplest case on a horizontal surface)
Ff = µN where N = mg cos Ø (on an inclined surface)
Ffs = µsN Ffk = µkN Ffr = µrN
F = ma w = mg

Where ...
F is Force 2, measured in Newtons (N)
w is Weight (it is a Force), measured in Newtons (N)
m is Mass, commonly measured in Kilograms (Kg), Grams (g) or Tonnes (t)
a is Acceleration (deceleration is negative), measured in Metres per Second squared (m/s2).
g or ag is the Acceleration due to Gravity and varies from 9.78 m/s2 (equator) to 9.83 m/s2 (North or South poles). The average value of gravity is taken to be either 9.80 m/s2 or 9.81 m/s2.
Ff is the Force of Friction, measured in Newtons (N).
µs µk & µr are Coefficients of Friction and are magnitudes without units.
N is the Normal Force, measured in Newtons (N).
Ffs is the Force of Static Friction, measured in Newtons (N).
Ffk is the Force of Kinetic Friction, measured in Newtons (N).
Ffr is the Force of Rolling Friction, measured in Newtons (N).
ø is the measure of the Incline of the Surface the object is resting on.
And
v is Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}[/latex] is Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
viis Initial Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}_{i}[/latex] is Initial Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vf is Final Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}_{f}[/latex]is Final Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
∆d is Distance travelled, commonly measured in Metres (m), Kilometres (km)
[latex]\Delta{\overrightarrow{d}}[/latex] is Change in Displacement, commonly measured in Metres (m), Kilometres (km) and includes a direction
a is Acceleration (deceleration is negative), measured in Metres per Second squared (m/s2)
[latex]\overrightarrow{a}[/latex] is Vector Acceleration, measured in Metres per Second squared (m/s2) and includes a directiont is Time, commonly measured in Seconds (s) or Hours (h)
Coefficients of kinetic friction
| MATERIALS | SURFACE CONDITIONS | µK |
|---|---|---|
| Glass on glass | clean | 0.9 - 1.0 |
| Wood on wood | clean and dry | 0.25 - 0.5 |
| Wood on wood | wet | 0.2 |
| Steel on steel | clean | 0.58 |
| Steel on steel | motor oil lubricant | 0.2 |
| Rubber on solids | dry | 1 -4 |
| Teflon on steel | clean | 0.04 |
| Waxed hickory on dry snow | 0.03 - 0.06 | |
| Brass on ice | 0.02 - |
13.1 Friction: 3, 4
Ffs = µsN Ffk = µkN Ffr = µrN
F = ma w = mg
The byproduct of friction is generally heat 5

Friction is a resistive force that acts to oppose the relative motion between two surfaces (objects, fluids, gases) that are moving or attempting to move past one another. Studies of friction find their origin in various Greek philosophers, such as Aristotle (384-322 BC), Victruvius (80 or 70 BC- 15 BC), and Pliny the Elder (23-79 AD), who were interested in both the causes of friction and how to reduce the amount of friction. The difference in frictional types of static and kinetic energy was known as early as Themistus (317-390 AD), who stated "it is easier to further the motion of a moving body than to move a body at rest".
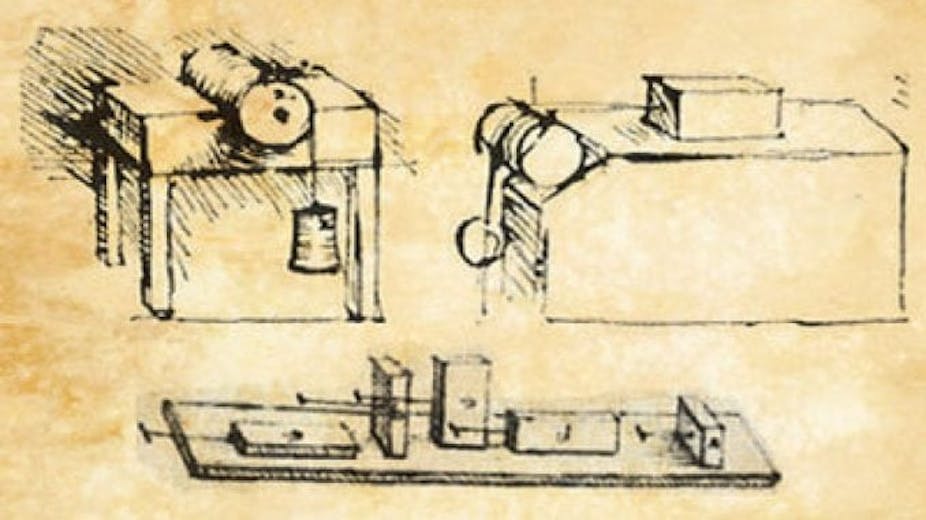
The first to develop the classic laws of friction was Leonardo da Vinci (1452-1519), who recorded his investigations using sketches of sliding blocks (shown above) on inclined surfaces. These ideas are still used today to demonstrate the fundamentals of friction that exists between solid bodies. Da Vinci’s works were never published and remained unknown until over 150 years later, when they were discovered again by Guillaume Amontons (1663-1705) and published as the Laws of Static Friction.
1st Law: The force of friction is directly proportional to the applied load.
2nd Law: The force of friction is independent of the apparent area of contact.
3rd Law: Kinetic friction is independent of the sliding velocity.
Amonton’s Laws can be demonstrated by objects such as a brick resting on an inclined plane. Bernard Forest de Bélidor (1698-1761) and Leonhard Euler (1707-1783) expanded the concept of friction from static to kinetic. Charles-Augustin de Coulomb (1736-1806) established that friction depended on several factors, such as the nature of the materials and coatings of the surfaces in contact, the weight or force of the load on the surface (Normal Force), and the length of time these surfaces remain in contact. The classical model of friction was completed by Arthur Morin (1795-1880) in his work on differences between sliding and rolling frictions, and Osborne Reynolds (1842-1912), who added the concept of friction that exists in the flow of fluids.
Current research is exploring the role of friction in earthquakes, artificial limbs and hip replacements, tiny sensors that control air bags, nanotech investigations of polymer molecules to create fluids to reduce friction, and even the role of rupture waves similar to sound waves that alter friction depending on the direction of motion. Some of the main motivations for this and other work are to increase the longevity and to reduce energy loss as we become more aware of the importance of conserving energy in devices. Studies of friction are important.
In this section, we will quantify static, kinetic and rolling frictions. The equations for these follow a pattern; the frictional force is a coefficient given by a standard symbolµ(value or ratio) of the Normal Force. The equations for all three of these frictions are shown below.
Ffs = µsN Ffk = µkN Ffr = µrN
In all cases, the symbol for friction is given by Ff with a subscript to distinguish which type of friction it is: sfor static, k for kinetic and r for rolling.
The Normal Force is often described as the support force of a surface or other stable object that is in contact with an object being supported. For an object on a desk or a chair, the Normal Force is the supporting force that acts to balance whatever force (generally gravity) that is holding the object to the surface. If a person pushes a book against a wall, then the Normal Force will be balancing this force.
Finding the coefficients of friction between two bodies is a complicated activity, since it is an attempt to quantify the relationship between the Frictional Force and the Normal Force. Technically, it is done through multiple experiments of two objects under similar conditions that can be affected by temperature, humidity, air pressure, dust, the types of solids, whether any fluids are present between the two surfaces, if the surfaces are flat and uniform, etc. In theory, the coefficient of friction also takes into account both mechanical interactions and actions at the atomic level.
The following examples explore introductory friction questions on a flat horizontal surface.
EXAMPLE 13.1.1
A 120 kg refrigerator rests on the floor. What applied force is required to move this refrigerator if µs = 0.15 exists between the refrigerator and the floor?
We need an applied force that is greater than the static frictional force.
F applied > Ffs (or µsN)
F applied > (0.15)(120 kg)(9.8 m/s2) cos 0°
F applied > 196 N (≈ 180 N)
EXAMPLE 13.1.2
An applied force of 420 N is needed to maintain the constant velocity of a 1200 kg car rolling along the street. What is the µr acting between this car and the road?
We need an applied force that equals the rolling frictional force.
F applied = Ffr (or µrN)
420 N = (µr)(1200 kg)(9.8 m/s2) cos 0°
µr = 420 N ÷ 11760 N
µr = 0.036
EXAMPLE 13.1.3
An applied force of 280 N is just enough to push a crate at a constant velocity on ice (mass of 140 kg). What is µk between this crate and the ice?
We need an applied force that equals the kinetic frictional force.
F applied = Ffk (or µkN)
280 N = (µk)(140 kg)(9.8 m/s2) cos 0°
µk = 280 N ÷ 1372 N
µk = 0.204
QUESTIONS 13.1 Friction - Questions
1. A 40 kg wooden crate rests on the floor. What applied force is required to set this crate in motion if μs = 0.50 exists between the crate and the floor?
2. An applied force of 300 N is needed to maintain the constant velocity of a 100 kg crate sliding across a warehouse floor. What is the μk acting between this crate and the floor?
3. An applied force of 200 N is just enough to start a motorcyclist and her bike rolling (combined mass of 500 kg). What is μr between this bike & rider and the road?
4. A truck that has a weight of 15 000 N is parked on a level road. If μs=0.48 what is the maximum frictional force with which this truck would resist an applied force?
5. A person is pulling a 25 kg sled horizontally. If the μk is 0.08, what horizontally applied force is needed to keep this sled moving at an average speed?
6. The engine of a 1200 kg car can accelerate with an unbalanced force of 10 000 N. What must be the minimum μs to prevent this car from spinning its tires?
13.2 Friction & Newton’s Second
Equations Used:
Ff = µN or “µmg” (simplest case)
Ff = µN where N = mg cos Ø
Ffs = µsN Ffk = µkN Ffr = µrN
F = ma w = mg
In this section of questions we explore the relationship between Net Force, Applied Force, Frictional Forces and Newton’s Second Law. Central to this is the concept that friction resists the vector sum of applied forces, and if there is an unbalanced force (Net Force) that results from the blend of applied forces and friction, then acceleration results. Quantified, this relationship looks as follows:
Fnet = F applied - Ff where Fnet = ma
The results of these calculations mean:
For an object at rest:
If Fnet = 0 then F applied = Ff
For an object in motion:
If Fnet > 0 then Fnet = ma and the object or system is accelerating.
If Fnet < 0 then Fnet = ma and the object or system is decelerating or remains in a
static situation.
One feature of interest is the role of friction in accelerating and decelerating. Friction will dictate the maximum value that some objects can accelerate or decelerate. An examples of this is the friction of tires on a road. The maximum rate of braking when decelerating depends on the friction that exists between the tires and the road. Likewise, the maximum rate that a vehicle can accelerate on a surface is dictated by the maximum friction that exists between the tires and the road. One can always add extra forces to complicate accelerating and decelerating but at the simplest:
acceleration & deceleration < maximum friction
If we are to summarize and put all the above on a sketch showing a change of applied force compared to friction as a function of time, then we would have something like:
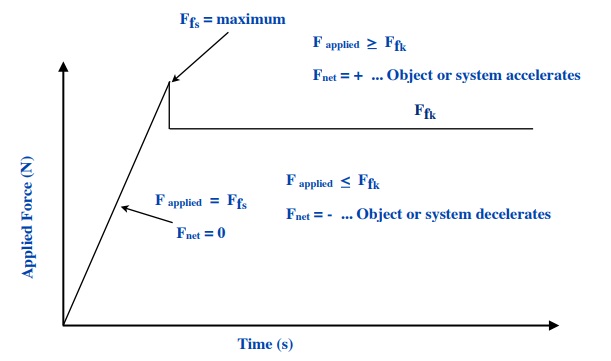
There are two distinct regions shown with five possibilities:
(i) If we are looking at how much force we are applying to an object at rest, the object will remain at rest until we are able to apply a force that is greater than the static force that resists it.
• When theF applied = Ffs and the object remains at rest or the Fnet = 0
• When the F applied > Ffs and the object will accelerate and the Fnet = ma
(ii) If we are looking at how much force we are applying to an object in motion, the object will react differently depending on how the applied force compares to the frictional force.
• When the F applied = Ffsand the object remains at constant speed or the Fnet = 0
• When the F applied > Ffs and the object will accelerate and the Fnet = ma
• When the F applied < Ffs and the object will decelerate and the Fnet = ma
EXAMPLE 13.2.1
A force of 170 N is applied to a 85 kg stove resting on the floor. (i) If this force is just enough to start it sliding, find µs. (ii) Find the acceleration of this stove (once moving) if µk drops to 0.15 and a force of 100 N continues to be applied. (Or does it continue to accelerate?)
(i) F applied = Ffs or µsmg cos ø
170 N = µs (85 kg)(9.8 m/s2) cos 0°
µs = 170 N ÷ 833 N
µs = 0.204 (≈ 0.20)
(ii) Fnet = F applied - Ffk
ma = 100 N - µkmg cos ø
(85 kg) a = 100 N - (0.15)(85 kg) (9.8 m/s2) cos 0°
(85 kg) a = 100 N - 125 N
a = - 25N ÷ 85 kg or - 0.29 m/s2
The Applied Force is not larger than friction and the stove will decelerate to a stop.
EXAMPLE 13.2.2
Suppose the grip of your car tires on clean pavement has a µs of 1.60. What is the maximum possible acceleration of your car using these tires?
Fnet = Ff where Fnet = ma and Ffs = µsN
This means that: ma = µsN in this case N = mg cos ø
ma = µs mg cos ø
Cancel out the common mass and we are left with
a = µs g cos ø
For horizontal surfaces we
a = (1.60)(9.80 m/s2) cos 0°
a = 15.7 m/s2
QUESTION 13.2 Friction and Newton's Second Law - Questions
1. Several people pushing together make a combined applied force of 1000 N on a 1200 kg car that has just started to roll. If μr is 0.04, find the resulting acceleration of this car.
2. A force of 200 N is applied to a 50 kg crate resting on the floor. (i) If this force is just enough to start it sliding, find μs. (ii) Find the acceleration of this crate (once moving) if μk drops to 0.3 and a force of 200 N continues to be applied.
3. Some of the best tires have a μs of 4.0. What is the maximum possible acceleration of cars that use these tires?
13.3 Friction & Accelerated Motion
Equations Used:
| [latex]a=\dfrac{\Delta{v}}{t}[/latex] | [latex]\overrightarrow{a}=\dfrac{\Delta{\overrightarrow{v}}}{t}[/latex] |
| [latex]\Delta{v} = v_{f} - v_{i}[/latex] | [latex]v =\dfrac{(v_{i} + v_{f})}{2}[/latex] |
| [latex]v_{f} = v_{i} + at[/latex] | [latex]2ad = v_{f}^{2} - v_{i}^{2}[/latex] |
| [latex]d = v_{i}t + ½ at^{2}[/latex] | [latex]d =\dfrac{(v_{i} + v_{f}) t}{2}[/latex] |
Ff = µN or “µmg” (simplest case)
Ff = µN where N = mg cos Ø
Ffs = µsN Ffk = µkN Ffr = µrN
F = ma w = mg

The following questions deal with situations where the Net Force is greater than zero, resulting in acceleration to the system being studied and where the Net Force is less than zero for any body in motion which results in the system decelerating. All equations have been used before in this textbook.
EXAMPLE 13.3.1
What distance is needed to bring a 1500 kg truck (traveling at 90 km/h) to a full stop on a rainy day if the µs between the tires and the wet road is 0.42?
The maximum deceleration is defined by the maximum static grip on the road. The frictional force in this problem is negative, since it is slowing the truck down to a stop.
Therefore FNet = - Ffs
ma = - µs mg cos ø
Cancelling out the common mass a = - µs g cos ø
a = - (0.42)(9.80 m/s2) cos 0°
a = - 4.12 m/s2
Now:
a = - 4.12 m/s2 Use 2ad = vf2 - vi2
vi = 90 km/h or 25 m/s 2 (- 4.12 m/s2) d = (0 m/s)2 - (25 m/s)2
vf = 0 m/s ... stopped (- 8.24 m/s2) d = - 625 m2/s2
d = find d = - 625 m2/s2
- 8.24 m/s2
t = not mentioned
d = 75.8 m (≈ 76 m)
EXAMPLE 13.3.2
A snowboarder traveling at 60 km/h slows to a speed of 5 km/h before stepping off the snowboard. If this snowboarder travels 20 m slowing down what was the average µk?
First:
a = find Use 2ad = vf2 - vi2
vi = 60 km/h or 16.7 m/s 2 a (20 m) = (1.39 m/s)2 - (16.7 m/s)2
vf = 5 km/h or 1.39 m/s (40 m) a = - 277 m2/s2
d = 20 m a = - 277 m2/s2
40 m
t = not mentioned
a = - 6.92 m/s2
Now ... FNet = - Ffk
ma = - µk mg cos ø
Cancelling out the common mass a = - µk g cos ø
- 6.92 m/s2 = -µk (9.80 m/s2) cos 0°
µk = - 6.92 m/s2 ÷ - 9.80 m/s2
µk = 0.71 (≈ 0.7)
EXAMPLE 13.3.3
A person is standing in the middle of an ice rink 12 m away from the boards. If the µs between this person’s feet and the ice is 0.080, what is the shortest amount of time this person would take to reach the boards?
First, we need to find the maximum acceleration from the grip on the ice that this person can achieve.
Therefore FNet = Ffs
ma = µs mg cos ø
Cancelling out the common mass a = µs g cos ø
a = (0.08)(9.80 m/s2) cos 0°
a = 0.784 m/s2
Now:
a = 0.784 m/s2 Use d = vit + ½ at2
vi = 0 m/s 12 m = (0 m/s)t + 1/2(0.784 m/s2)t2
vf = not mentioned 12 m = (0.392 m/s2) t2
d = 12 m [latex]t^{2} =\dfrac{12 m}{0.392 m/s^{2}}[/latex]
t = find
t = 5.5 s
QUESTIONS 13.3 Friction and Accelerated Motion
1. A hubcap leaves a moving car traveling at 40 km/h and rolls for 200 m before coming to a full stop. What is the average μr acting on this hubcap?
2. (i) What distance is needed to bring a 1200 kg car (traveling at 100 km/h) to a full stop if the μs between the tires and the road is 0.38? (ii) What distance would this car skid if the μk between its tires and the road is 0.26?
3. A skier on wet snow experiences a μk of 0.10. What would be the maximum distance this skier would travel on level ground before stopping if he/she had an initial speed of 35 km/h?
4. A water skier traveling at 50 km/h slows to a speed of 10 km/h before sinking under water. If this skier travels 50 m while slowing down what was the average μk?
5. With a μk of 0.05 what distance will an ice skater traveling at 18 m/s glide before coming to a full stop?
6. A snow skier traveling at 45 km/h slows to a stop over a horizontal distance of 350 m. What was the average μk?
7. A person is standing in the middle of an ice rink 20 m away from the boards. If the μs between the person's shoe and ice is 0.04, what is the shortest amount of time this person would take to reach the boards?
8. A 80 kg person is standing on ice, where the coefficients of friction between the person'.s shoe and ice are μs = 0.06. If a 10 kg medicine ball is thrown to this person to catch at a speed of 4.0 m/s, is the person going to be able to stand still? (It takes 0.50 s for the person to bring this ball to a full stop.)
9. In a lawn bowling game, a 3.5 kg bowling ball that is rolling at 4.2 m/s travels 18 m before coming to a stop. What is the average frictional force that is acting on the bowling ball?
13.4 Friction on an Inclined Surface 6
Equations Used: Basic Trigonometric Ratios
[latex]Sin =\dfrac{Opposite}{Hypotenuse} Cos =\dfrac{Adjacent}{Hypotenuse} Tan =\dfrac{Opposite}{Adjacent}[/latex]
Ff = µN where N = mg cosØ
Ffs = µsN Ffk = µkN Ffr = µrN
F = ma w = mg
When we consider multiple forces acting on a body or a system we are drawing what is known as Free Body Diagrams.7 Free body diagrams represent a picture of the forces that are acting on a body or a system. In the examples below, the forces illustrated are friction, applied forces, the Normal force, and weight.
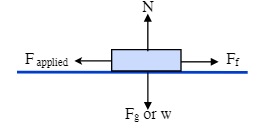
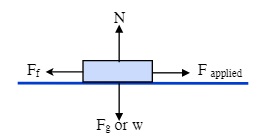
You can see for these situations that the angle of the incline is 0° and as such cos 0° =
1. Because of this, introductory physics students often remember the Normal force as equaling
N = mg instead of the proper N = mg cos ø, where the only force holding the object to the surface is gravity. This is a request for you as students to use the equation for Normal Force as given by the equation: N = mg cos ø
Examples on the next page illustrate the Normal Force on horizontal and inclined surfaces.
These diagrams become a little more complicated when used to analyze objects on inclined surfaces.
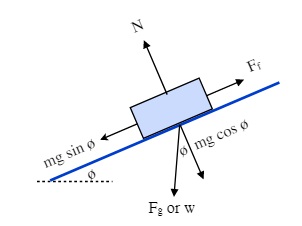
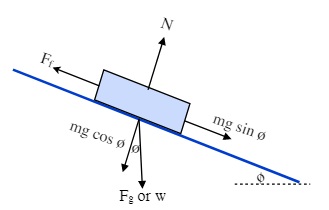
Both of these examples are nearly identical to the previous Free Body Diagrams, except that they now take the weight vector and break it up into the force that is pulling the object directly into the surface and the part of the force that is now acting to pull the object down the plane.
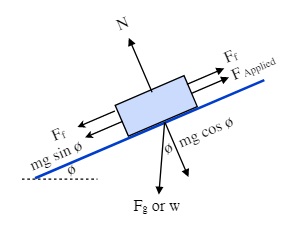
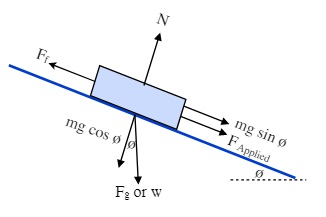
These Free Body diagrams8 can be also drawn showing Forces that act in either direction, both up and down the inclined surface. As above, the Free Body Diagrams are identical to the ones above with one addition, the applied force and the direction of the frictional force. The frictional force will always act opposite to the net force between applied force and the force of gravity pulling the object down the incline. In the example to the left, the frictional force is shown as acting either up or down the incline. Friction in this case acts opposite to the direction of the vector sum of the applied force and the force of gravity pulling down the incline.
EXAMPLE 13.4.1
Draw the Free Body diagram for the following questions using the data given
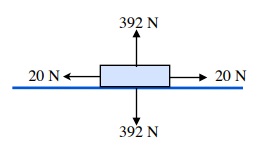
1. m = 40 kg, F Applied = Ffs = 20 N
N = mg cos ø
N = (40 kg)(9.80 m/s2) cos 0°
N = 392 N
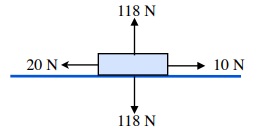
2. m = 12 kg, F Applied 20 N (left), Ffs = 8 N (right)
N = mg cos ø
N = (12 kg)(9.80 m/s2) cos 0°
N = 118 N
3. m = 8 kg, FApplied 20 N (down), Ff = 32 N (up), ø = 15°
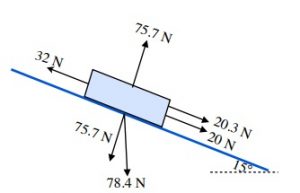
w = mg
w = (8 kg)(9.80 m/s2)
w = 78.4 N (≈ 78 N)
N = mg cos ø
N = (8 kg)(9.80 m/s2) cos 15°
N = 75.7 N (≈ 76 N)
Fd = mg cos ø
Fd = (8 kg)(9.80 m/s2) sin 15°
Fd = 20.3 N (≈ 20 N)
EXAMPLE 13.4.2
A truck is coasting downhill on a steep slope angled at 7°, maintaining a constant speed. If the coefficient of rolling friction is µr = 0.07, and the truck and driver have a mass of 1750 kg, what is the average braking force that is needed?
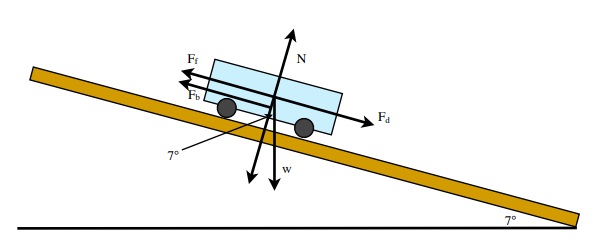
For this problem, the forces we need to work with are:
Fd = mg sin Ø Ffr = µrN or µrmg cos Ø and Fb = find
Equating them yields:
Ffr + Fb = Fd
Which expands to:
µr mg cos Ø + Fb = mg sin Ø
(0.07)(1750 kg) 9.80 m/s2) cos 7° + Fb = (1750 kg) 9.80 m/s2) sin 7°
1192 N + Fb = 2090 N
Fb = 2090 N - 1192 N
Fb = 898 N
QUESTIONS 13.4 Friction on an Inclined Surface
1. A car is rolling downhill on a road angled at 6°. If the coefficient of rolling friction is μr = 0.05, and the car and driver have a mass of 1450 kg, what is the average acceleration of the car and driver?
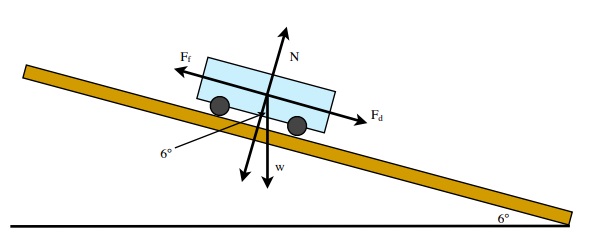
2. A car is coasting downhill on a steep slope angled at 8°, maintaining a constant speed. If the coefficient of rolling friction is μr = 0.08, and the car and driver has a mass of 1350 kg, what is the average braking force that is needed?

3. A block is at rest on a board that is being raised at one end. At a certain angle Ø the block begins to slide. If the coefficient of static friction is μs = 0.42, what is the angle Ø that the block begins to slide?
REFERENCES

