Chapter 12: Power, Work and Energy

Equations Introduced and Used for this Topic:
| [latex]a =\dfrac{\Delta{v}}{t}[/latex] | [latex]\overrightarrow{a} =\dfrac{\Delta\overrightarrow{v}}{t}[/latex] |
| [latex]\Delta{v} = v_{f} - v{i}[/latex] | [latex]v =\dfrac{(v_{i }+v_{f}}{2}[/latex] |
| [latex]v_{f} = v_{i} + at[/latex] | [latex]\text{2 ad} = v_{f}^{2} - v_{i}^{2}[/latex] |
| [latex]d = v_{i}^{t} = 1/2 at^{2}[/latex] | [latex]d =\dfrac{v_{i} + v_{f})t}{2}[/latex] |
| [latex]\text{F = ma}[/latex] | [latex]\text{w = mg}[/latex] |
Work (W) = F • d or F d cosØ W = ∆ Energy
Ep = mgh V or Vg = gh Ek = ½ mv2
Power (P) =[latex]\dfrac{W}{t} =\dfrac{\Delta{Energy}}{t}[/latex]
P = ½ ρ A v3 Efficiency =[latex]\dfrac{Output}{Input}[/latex] x 100%
Where:
P is the Power, measured in Watts (W)
W is Work, measured in Joules (J)
ρ is the Density of the Moving Medium, measured in Kilograms per Metre cubed (kg/m3)
A is the Cross Sectional Area of the turbine, measured in Metres squared (m2)
v is the Speed of the Medium moving through the turbine, measured in Metres per Second (m/s)
v is the Speed of the object commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
∆ Energy is the change in Energy and can be any form of Energy (Ep, Ep or other forms), measured in Joules (J)
Ep is Gravitational Potential Energy, measured in Joules (J)
Ek is Kinetic Energy, measured in Joules (J)
V or Vg is the Gravitational Potential, measured in Newtons per Kilogram (N/kg)
∆h is the change in Vertical Height, measured in Metres (m)
F is Force, measured in Newtons (N)
m is Mass, commonly measured in Kilograms (Kg), Grams (g) or Tonnes (t)
g or ag is the Acceleration due to Gravity and varies from 9.78 m/s2 (equator) to 9.83 m/s2 (North or South poles). The average value of gravity is taken to be either 9.80 m/s2 or 9.81 m/s2 .
[latex]\overrightarrow{v}[/latex] is Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vi is Initial Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}_{i}[/latex] is Initial Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vi is Final Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}_{f}[/latex] is Final Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
∆d is Distance travelled, commonly measured in Metres (m), Kilometres (km)
[latex]\Delta\overrightarrow{d}[/latex] is Change in Displacement, commonly measured in Metres (m), Kilometres (km) and includes a direction
a is Acceleration (deceleration is negative), measured in Metres per Second squared (m/s2)
[latex]\overrightarrow{a}[/latex] is Vector Acceleration, measured in Metres per Second squared (m/s2) and includes a direction
t is Time, commonly measured in Seconds (s) or Hours (h)
12.1 Power 4
Work (W) =[latex]\overrightarrow{F} •\overrightarrow{d} or\overrightarrow{F}\overrightarrow{d}[/latex] cosØ W = ∆ Energy
Power (P) =[latex]\overrightarrow{F} •\overrightarrow{v}[/latex] Power (P) = [latex]\dfrac{W}{t} =\dfrac{\Delta{Energy}}{t}[/latex]
Power is the rate at which work is done on a system or the rate of energy transfer between systems. Rate refers to the amount of change in some measure of time.
1 Watt = 1 Joule/Second
The concept of power originated from the studies of James Watt (1736-1819) as a way to compare the work done between steam engines and horses. This comparison was done in the absence of modern SI units, and with no energy concept (James Joule was 8 months old when Watt passed away). Instead, Watt defined his measure of power as the product of Force and Velocity, as a way of relating his steam engines to horses. As such, the first measure of power used units of the pound to measure force and inches per second, feet per minute and miles per hour.
Power (P) = Force x Velocity
Watt’s work, therefore, defining power in terms of horsepower equivalents,
specifically:
one horsepower (hp) equaled the power to raise 33,000 pounds (lbs) 1 foot (ft) per minute (550 pounds 1 foot per second).
Legend has it that one of Watt’s first customers for his significantly improved steam engine5 asked Watt to compare it to a horse, which happened to be his strongest and most powerful horse. Not only was Watt’s steam engine more powerful than this horse, the units of horsepower were then defined in terms of the power of this horse.
CAN NOT FIND PICTURE OF THE BREWER HOUSE

Since Watt originally defined the value of horsepower, two measures are commonly used:
Mechanical Horsepower = 745.69987158227022 W (≈ 746 W)
and
Metric Horsepower = 735.49875 W (≈ 735 W)
In this textbook, mechanical horsepower will be used, since it is the most common in public usage. Electrical horsepower6 is defined as 746 W. Questions concerning power will use the following two equations:
Mechanical Power (Conservative Forces) [latex]\text{P =}\dfrac{\overrightarrow{F}•\overrightarrow{d}}{t}[/latex]
Average Power [latex]\text{P =}\dfrac{W}{t}[/latex]
EXAMPLE 12.1.1
A 300 hp (horsepower) engine is equivalent to how many watts?
Simple Conversion: 300 hp = 300 hp x 746 W/hp
300 hp = 224 000 W
EXAMPLE 12.1.2
If 3.0 MJ of work is done in 2 min what is the power involved?
P = find [latex]\text{P =}\dfrac{W}{t} =\dfrac{\Delta{Energy}}{t}[/latex]
W = 3.0 x 106 J
[latex]\text{P =}\dfrac{3.0\times10^{6}J}{120 s}[/latex]
t = 2 min or 120 s
P = 25 000 W or 25 kW
EXAMPLE 12.1.3
How much work can a 746 W motor do in 8.0 h?
P = 746 W 746 W =[latex]\dfrac{W}{(8.0)(3600 s)}[/latex]
W = find
W = (746 W)(8.0)(3600 s)
t = 8.0 h or (8.0)(3600 s)
W = 2.148 x 107 J (≈ 2.1 x 107 J)
EXAMPLE 12.1.4
What minimum amount of time would it take a 200 W electric motor to do 12000 J of work?
P = 200 W [latex]\text{P =}\dfrac{W}{t} =\dfrac{\Delta{Energy}}{t}[/latex]
W = 12 000 J
200 W =[latex]\dfrac{12 000 J}{t}[/latex]
t = find
t = 12 000 J ÷ 200W
t = 60 s
EXAMPLE 12.1.5
If only 84% of the force produced by a 1200 W electric motor is conservative, how much time is required to do 50 000 J of work?
P = 1200 W P =[latex]\dfrac{w}{t} =\dfrac{\Delta{Energy}}{t}[/latex]
W = 50 000 J
(0.84)(1200 W) = [latex]\dfrac{(50 000 J)}{t}[/latex]
t = find
efficiency = 84% or 0.84 t = 50 000 J ÷ 1008W
t = 49.6 s (≈ 50 s)
QUESTIONS 12.1 Power
1. If 3 x 106J of work is done in 5 min what is the power involved?
2. How much work can a 25 W motor do in 60 h?
3. What is the minimum amount of time that it would take a 500 W electric motor to do 15 kJ of work?
4. 120 hp (horsepower) is equivalent to how many watts?
12.2 Power & Change in Energy
Work (W) =[latex]\overrightarrow{F}•\overrightarrow{d} or\overrightarrow{F}\overrightarrow{d}[/latex] cosØ W = ∆ Energy
Power (P) =[latex]\overrightarrow{F} •\overrightarrow{v}[/latex] Power (P) = W =[latex]\dfrac{\Delta}{Energy}[/latex]
Ep = mgh V or Vg = gh Ek = ½ mv2
When the force used in power settings is conservative, then the work done by this power results in a change of mechanical energy and as a result changes either the kinetic, potential or both types of mechanical energies in a system.
EXAMPLE 12.2.1
A conveyor belt carries a flat of 500 kg of asphalt shingles at a constant speed from the ground to the roof of a building 8.0 m above its initial position in 12.0 s. Find the work done on the object and the power required to accomplish it. (Assume the initial and final speeds of these shingles are zero.)
W = ∆ Energy = ∆ Ep or mg∆h Power (P) =[latex]\dfrac{W}{t}[/latex]
W = (500 kg)(9.8 m/s2)(8.0 m)
P =[latex]\dfrac{39200 J}{12.0 s}[/latex]
W = 39200 J
P = 3270 W (≈ 3300 W)
EXAMPLE 12.2.2
What is the power of an air cannon that can fire a seed pellet (mass 45.0 g) from rest to a speed of 140 km/h in 0.125 s?
Power (P) =[latex]\dfrac{W}{t}=\dfrac{\Delta{Energy}}{t}[/latex] where ∆ Energy = Ekf - Eki where Eki = 0J
[latex]P =\dfrac{½ mV_{f}^{2}}{t}[/latex]
[latex]P =½\dfrac{(\text{0.045 kg})(\text{38.9 m/s})^{2}}{0.125s}[/latex]
EXAMPLE 12.2.3
What is the expected power output that can be achieved from an 85.0 m high hydroelectric dam7 where the rate of water moving through the generators is 900 cubic metres per minute? If the efficiency of electric power production is 32%, what is the power produced?
[latex]Power (P) =\dfrac{W}{t}=\dfrac{\Delta{Energy}}{t}[/latex] where ∆ Energy = ∆ Ep or mg∆h
[latex]P =\dfrac{mg\Delta{h}}{t}[/latex]
[latex]P =\dfrac{(900 m^{3})(1000 kg/m^{3}(9.8 m/s^{2})(85 m)}{60 s}[/latex]
P = 1.25 x 107 W or 12.5 MW
At 32% efficiency, the power generated is:
P = (0.32)(12.5 MW) or 4.0 MW
The mechanical advantage of pulleys is not covered in this textbook. Using pulleys, one can increase the load being raised by using the same power source. In this case, you can see the amount of rope (displacement) that is being used by smaller forces to do the same amount of work. This means that less powerful engines can be used to do the same amount of work, albeit at a slower rate. In the example shown below, each pulley adds to the displacement that the force acts through. In this case one only needs to consider the amount of energy lost to friction and other forces.
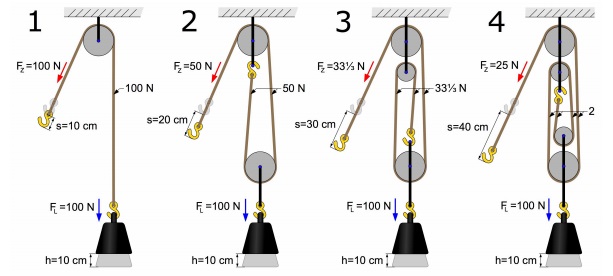
QUESTIONS 12.2 Power and Change in Energy
12.3 Power & Accelerated Motion
Equations Used:
| [latex]a =\dfrac{\Delta{v}}{t}[/latex] | [latex]\overrightarrow{a}\dfrac{\Delta\overrightarrow{v}}{t}[/latex] |
| [latex]\Delta{v} = v_{f} - v_{i}[/latex] | [latex]v =\dfrac{(v_{i}+ v_{f})}{2}[/latex] |
| [latex]v_{f} = v_{i }+ at[/latex] | [latex]2ad = v_{f}2 - v_{i}2[/latex] |
| [latex]d = v_{i}t + ½at^{2}[/latex] | [latex]d =\dfrac{(v_{i} + v_{f})}{2}[/latex] |
| [latex]\text{F = ma}[/latex] | [latex]\text{w = mg}[/latex] |
| [latex]\text{Work (W) = F • d or F d cos Ø}[/latex] | [latex]\text{W = ∆ Energy}[/latex] |
Ep = mgh V or Vg = gh Ek = ½ mv2
[latex]Power (P) =\dfrac{W}{t}\dfrac={\Delta{Energy}}{t}[/latex]
Power, when referring to the rate of work being done by a conservative force, implies a change in mechanical energy, be it kinetic or potential (or both). When we restrict ourselves to only examining conservative forces, the system can be accelerating, changing vertical height at a constant velocity, or a more complicated combination of both kinetic and potential energies.
In the following examples using conservative forces, power is expanded to explore both accelerating and constant velocity situations.
EXAMPLE 12.3.1
A motor is rated to deliver 8.4 kW. What is the constant speed that this motor can raise a mass of 2100 kg?
[latex]Power (P) =\dfrac{W}{t} =\dfrac{\Delta{Energy}}{t}[/latex] where ∆ Energy = ∆ Ep or mg∆h
[latex]P =\dfrac{mg\Delta{h}}{t}[/latex] or ... P = mg vup or P = mg vy
8400 W = (2100 kg)(9.8 m/s2)(vy)
vy = 8400 W ÷ [(2100 kg)(9.8 m/s2)]
vy = 0.41 m/s
EXAMPLE 12.3.2
A jet car used in drag racing took 3.4 seconds to travel 400.0 m from a stationary start. If this car had a mass of 0.95 tonnes:
(i) Calculate the unbalanced force accelerating this car.
(ii) What power was developed?
(i) First, we need to calculate the acceleration.
First find the acceleration:
d = vit + 1/2 at2
400 m = (0 m/s)(3.4 s) + 1/2 (a)(3.4 s)2
a = 69.2 m/s2
Second, find the force.
F = m a
F = (950 kg)(69.2 m/s2)
F = 65 700 N (≈ 66 000 N)
(ii)
[latex]Power (P) =\dfrac{w}{t} =\dfrac{\Delta{F}d cosø}{t}[/latex]
[latex]P =\dfrac{(65 700 N)(400 m) cos 0^{º}}{3.4 s}[/latex]
P = 7.73 x 106 W or 7.73 MW (≈ 7.7 MW)
EXAMPLE 12.3.3
A machine can produce 120 W of power. If the machine is used for 12 s to raise a 50 kg mass straight upwards from a platform, where it is then released, at what speed would you expect this mass to impact the platform?
This problem is simpler than it looks. Since the work using conservative forces is a change in potential energy, and in the second part where it is dropped, the potential energy changes to kinetic energy, then one can just use the work-energy theorem to solve this one. There is no need to determine the change in potential energy, which we would then use to find the change in potential energy.
Therefore:
[latex]Power (P) =\dfrac{W}{t}[/latex] or W = P t
where W = ∆Ek or W = (Ekf - Eki)
we are left with P t = 1/2 mvf2 - 1/2 mvi2
(120 W)(12 s) = 1/2 (50 kg) vf2 - 1/2 (50 kg)(0 m/s)2
vf2 = 1440 Ws ÷ 25 kg
vf = 7.6 m/s
EXAMPLE 12.3.4
A 2.0 kW powered conveyer belt machine is angled at 28° above the horizontal. At what constant speed can this belt be moving a 120 kg crate?
For this problem, we need to use the definition of Power = Force x Velocity cos ø, where the angle ø in this problem is between the force and velocity, and is 90° - 28° or 62°
Therefore: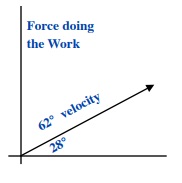
Power (P) = F • v cos ø where F = weight of 120 kg
2000 W = (120 kg)(9.8 m/s2)(v) cos 62°
v = 2000 W ÷ 552 J
v = 3.6 m/
QUESTIONS 12.3 Power and Accelerated Motion
1. A motor is rated to deliver 10 kW. What is the constant speed that this motor can raise a mass of 2.75 x 104 kg?
2. What is the maximum possible constant speed that a 120 hp engine could lift a 4 ton (metric) mass straight up?
3. What power is needed to run an elevator (maximum mass of 3500 kg, elevator and passengers) that rises at an average speed of 0.4 m/s?
4. A cement pump can lift concrete at the rate of 3500 kg up 20 m every minute.
(i) What would be the minimum power of this pump?
(ii) If this pump is 25% efficient, what minimum power must it be?
5. A monster truck used in drag racing took 15.0 seconds to travel 400.0 m from a stationary start. If this truck had a mass of 2.40 tonnes:
(i) Calculate the unbalanced force accelerating this truck.
(ii) What power was developed?
6. An engine can produce 25 000 W of power. If we assume that the conversion of engine power to mechanical energy of this 1000 kg car is 100% efficient, at what speed could this car be traveling after 15 s of full power starting from rest?
7. A machine can produce 40 W of power. If the machine is used for 15 s to raise a 20 kg mass straight upwards, where it is released, at what speed would you expect this mass to impact its starting position?
8. If a loaded semi (total mass = 20,000 kg) is able to maintain a constant speed of 20 km/h up an 8° inclined road, what is the power output of the truck’s engine?
9. What is the angle of a hill that a loaded pickup truck (m = 3600 kg) can climb at a constant speed of 45 km/h, if the 300 hp engine is 32% efficient?
QUESTIONS 12.4.1 - 12.4.3
12.4.1 Large trees can evaporate as much as 1000 kg of water per day. Assuming the average rise of water to be 10 m from the ground, what amount of energy must be supplied for this? If we assume the source of this energy is from the sun, what average amount of power must the tree receive over 12 hours of sunlight?
12.4.2 An average human at rest radiates 75 W of power. What amount of energy is radiated in eight hours?
12.4.3 Power Output of the Sun. The amount of solar energy striking the Earth is around 1350 Watts per metre2. Find the power output of our sun.

Under Business as Usual projections for global energy consumption, Energy usage is expected to rise from 589 EJ in 2016 to 1070 EJ in 2100 (E stands for exo x 1021).
Video File - NASA - SDO Year 5: https://www.youtube.com/watch?v=GSVv40M2aks
12.4.4 The Wind Resource8, 9
Several factors can affect wind speed and the ability of a turbine to generate more power. For example, wind speed increases as the height from the ground increases. If wind speed at 10 meters off the ground is 6 m/s it will be about 7.5 m/s at a height of 50 meters. A 2003 Stanford University study examined wind speeds at higher elevations and found that as much as one quarter of the United States, including areas historically thought to have poor wind potential, is potentially suitable for providing affordable electric power from wind. The rotors of the newest wind turbines can now reach heights up to 70 meters. In addition to height, the power in the wind varies with temperature and altitude, both of which affect the air density. Winter winds in Minnesota State will carry more power than summer winds of the same speed high in the passes of the Southern States.
The more the wind blows, the more power will be produced, with the main drawback being inconsistent wind. The term used to describe this is "capacity factor", which is simply the amount of power a turbine actually produces over a period of time divided by the amount of power it could have produced if it had run at its full-rated capacity over that time period.
A more precise measurement of output is the "specific yield". This measures the annual energy output per square meter of area swept by the turbine blades as they rotate. Overall, wind turbines capture between 20 and 40 percent of the energy in the wind. So, at a site with average wind speeds of 7 m/s, a typical turbine will produce about 1100 kilowatt-hours (kWh) per square meter of area per year. If the turbine has blades that are 40 meters long, for a total swept area of 5029 square meters, the power output will be about 5.5 million kWh for the year. An increase in blade length, which in turn increases the swept area, can have a significant effect on the amount of power output from a wind turbine.
Another factor in the cost of wind power is the distance of the turbines from transmission lines. Although some large windy areas, particularly in rural parts of the High Plains and Rocky Mountains, are too far from power lines to be cost-effective today, the potential for these regions is still enormous.
A final consideration for a wind resource is the seasonal and daily variation in wind speed. If the wind blows during periods of peak power demand, power from a wind farm will be valued more highly than if it blows in off-peak periods. In California, for example, high temperatures in the central valley and low coastal temperatures near San Francisco cause powerful winds to blow across the Altamont in the summer, a period of high power demand.
EXAMPLE 12.4.1

What is the kinetic energy or the air mass that passes through an offshore windmill at the Thorntonbank Wind Farm10, having a rotor diameter of 126 m, if the wind speed averages 30 km/hr? If we assume that current technology yields 45% power generation from this moving air mass, what power is produced per turbine?
Kinetic Energy:
Ek = ½ mv2
Ek = ½ (1.225 kg/m3)(8.33 m/s)2
Ek = 42.5 J/m3
Power Produced (100% Efficient):
P = ½ ρ A v3
P = ½ (1.225 kg/m3)(π)(126 m)2(8.33 m/s)3
P = 1.77 x 107 W or 17.7 MW (≈ 18 MW)
Now, for 45% efficiency:
P = (0.45)1.77 x 107 W
P = 7.95 x 106 W or 7.95 MW (≈ 8.0 MW)
Wind Turbine Power:
P = ½ ρ A Cp v2 Ng Nb
Where:
P = power in watts
ρ = air density (about 1.225 kg/m3 at sea level at 15°C)
A = rotor swept area exposed to the wind (m2)
Cp = Coefficient of performance (0.59 {Betz limit} is the maximum theoretically possible 0.35 for a good design)
v = wind speed in m/s
Ng = generator efficiency (50% for car alternator, 80% or possibly more for a permanent magnet generator or grid-connected induction generator)
Nb = gearbox/bearings efficiency (could be as high as 95% if good)
Temperature (°C )12
-25 -20 -15 -10 -5 0 5 10 15 20 25 30 35
1.423 1.395 1.368 1.342 1.317 1.292 1.269 1.247 1.225 1.204 1.184 1.164 1.146
Density of Air (kg/m3)
QUESTIONS 12.4.4 The Wind Resource
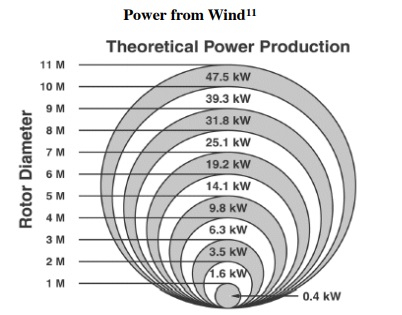
1. Using the graph and the chart on the previous page and assuming 100% efficiency:
(i) What is the area of a 1.0 m circle?
(ii) If the density of air at 20° C is 1.204 kg/m3 at sea level what must be the minimum speed of the air for the 1.0 m diameter rotors to extract 0.4 kW?
(iii) Using an air temperature of 20°C, calculate the minimum number of 11 m diameter rotors needed to generate 20 MW?
(iv) What must be the speed of the air at -15°C to create 0.4 kW?
(v) Assuming the 10 m rotor produces 39.3 kW at an air temperature of 20°C, what is the percent increase in power output if the temperature drops to -20°C?
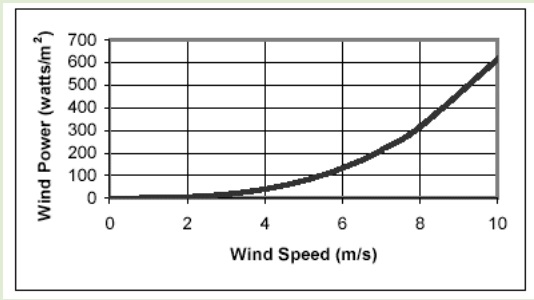
2. The above graph shows the potential amount of energy from wind at 20° C.
(i) What would this curve look like if the air is hotter?
(ii) What would this curve look like if the air is colder?
(iii) Notice the power at 8.0 m/s is around 300 W and at 10 m/s around 600 W. Show how these numbers fit the equation:
P = ½ρ A v3
(iv) How big would the rotor area of the windmill graphed above be if we assume it is 100% efficient?
(Realistically, Cp Ng Nb = 0.27 or is around 27%)
INSERT GRAPH AND MAP OF CANADA
12.4.5 Power from Ocean and River Currents13, 14
Ocean current speeds are generally lower than wind speeds. This is important because the kinetic energy contained in flowing bodies is proportional to the cube of their velocity. However another more important factor in the power available for extraction from a flowing body is the density of the material. Water is about 835 times denser than wind, so for the same area of flow being intercepted, the energy contained in a 19 km/h water flow is equivalent to that contained in an air mass moving at about 180 km/h. Thus, ocean currents represent a potentially significant, currently untapped reservoir of energy.
The total worldwide power in ocean currents has been estimated to be about 5000 GW, with power densities of up to 15 kW/m2. The relatively constant extractable energy density near the surface of the Florida Straits Current is about 1 kW/m2 of flow area. It has been estimated that capturing just 1/1000th of the available energy from the Gulf Stream, which has 21 000 times more energy than Niagara Falls in a flow of water that is 50 times the total flow of all the world’s freshwater rivers, would supply Florida with 35% of its electrical needs.
Countries that are interested in pursuing the application of ocean current energy technologies
include the European Union, Japan and China.
P = ½ ρ A v3
Equation Introduced:
P = ½ ρ A v3
Where:
P = power in watts
ρ = density of water (fresh water is roughly 1000 kg/m3)
A = rotor swept area exposed to the water (m2)
v = water speed (m/s)
EXAMPLE 12.5.1
The Amazon River can reach an average current speed of 7 km/h at the height of the wet season. What is the expected power that can be produced by an underwater turbine of diameter 2.0 m, assuming an efficiency of 42% for the power generating turbine? (Density of fresh water is around 1000 kg/m3.)

P = ½ ρ A v3
P = ½(1000 kg/m3) π (2.0 m)2 (1.94 m/s)3
P = 12 200 W
or 12.2 kW (≈ 12 kW)
QUESTIONS 12.4.5 Power from Ocean and River Currents
1. The Fraser River has an average current speed ranging from 0.25 m/s to 1.25 m/s. What is the expected range of power that can be produced by an underwater turbine of diameter 1.5 m? (Density of fresh water is around 1000 kg/m3.)
2. One of the strongest ocean currents is the Gulf Stream, which moves at speeds greater than 1.5 m/s. What is the maximum power that can be extracted by a 3.0 m diameter underwater turbine in this current? How many of these turbines would be needed to replace a 50 MW coal-powered electric generator? (Density of ocean water is around 1003 kg/m3.)
3. What maximum power could be extracted from a 1.0 m diameter turbine in water moving at 20 km/h (this is the speed of water falling 1.57 m)? How does this compare to what a similar sized turbine could extract from a Category 2 Hurricane, where the wind (20° C) is moving at 160 km/h?
INSERT POLAR ICE PACK PICTURE
"If we could harness 0.1 percent of the energy in the ocean15 we could support the energy needs of 15 billion people."
REFERENCES:
1. A-Level Physics Tutor: http://www.a-levelphysicstutor.com/index-mech.php
2. Image Source: https://beyondconstruction.no/baerekraft/skepsis-og-myter-rundt-tre-som-byggemateriale/
3. Article to Read - Bye Aerospace’s Sun Flyer 2 completes first flight with Siemens electric propulsion motor: https://www.greencarcongress.com/2019/02/20190219-bye.html
4. Extra Help - Power: https://www.physicsclassroom.com/class/energy/Lesson-1/Power
5. Watt’s improvements on the steam engine efficiency is credited to be the start of the expansion of the industrial revolution. The unit of Watts to measure power was named in honor of James Watt for his steam engine improvements in 1889.
6. Wikipedia has an extensive list of the various form and measures of horsepower: https://en.wikipedia.org/wiki/Horsepower
7. Fact Sheet - Niagara Falls FAQ: http://nyfalls.com/niagara-falls/faq5/
9. In Research News - Europe has the untapped onshore capacity to meet global energy demand: https://www.sciencedaily.com/releases/2019/08/190814081202.htm
10. Thorntonbank Wind Farm : https://en.wikipedia.org/wiki/Thorntonbank_Wind_Farm
11. Source ...http://www.totalalternativepower.com/faq.htm
12. http://en.wikipedia.org/wiki/Density_of_air
13. Technology White Paper on Ocean Current Energy Potential on the U.S. Outer Continental Shelf, May 2006
14. In Research News - Hunt, J. D., et al. (2019) Using the jet stream for sustainable airship and balloon transportation of cargo and hydrogen: https://www.sciencedirect.com/science/article/pii/S2590174519300145
15. Article to Read - Scientists Develop Wave Energy Device That Generates Low-Cost Electricity: https://oilprice.com/Latest-Energy-News/World-News/Scientists-Develop-Wave-Energy-Device-That-Generates-LowCost-Electricity.html

