Chapter 1: Measurement Conversions
Distance:
12 in = 1 ft 1 inch = 2.54 cm 10 mm = 1 cm
3 ft = 1 yd 1 ft = 0.3048 m 1000 mm = 1 m
1760 yd = 1 mi 1 mile = 1.602 km 100 cm = 1 m
5280 ft = 1 mi 1 Nautical Mile = 1852 m 1000 m = 1 km
Area:
144 in 2 = 1 ft2 1 in2 = 6.45 cm210,000 cm2 = 1 m2
43,560 ft2 = 1 acre 1 ft2 = 0.092903 m210,000 m2 = 1 hectare
640 acres = 1 mi2 1 mi2 = 2.59 km2100 hectare = 1 km2
Volume:
57.75 in3 = 1 qt16.39 cm3 = 1 in31 cm3 = 1 ml
4 qt = 1 gal 1 ft3 = 0.0283168 m31000 ml = 1 liter
42 gal (oil) = 1 barrel 3.79 liters = 1 gal 1000 liter = 1 m3
Mass/Weight:
437.5 grains = 1 oz 453 g = 1 lb.1000 mg = 1 g
16 oz = 1 lb.2.2 lb. = 1 kg1000 g = 1 kg
2000 lb. = 1 short ton 1000 kg = 1 metric ton
Time:
1 h = 60 min1 min = 60 s1 yr = 365.2425 day (average)
1 h = 3600 s1 day = 24 h1 yr = 365.25 day (Astronomical)
Temperature:
Fahrenheit - Celsius Conversions: °C = 5/9 (°F - 32)and °F = 9/5 (°C + 32)

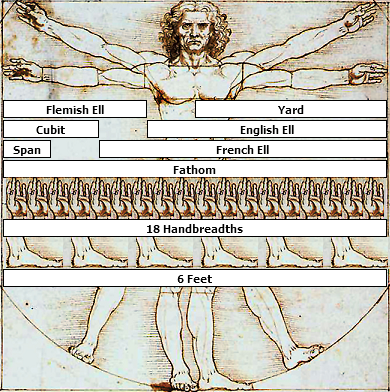
There is a short story written by Isaac Asimov in 1964 where he describes measures drawn from a 1785 text by Nicholas Pyke:

“A great deal of Pyke’s book consists of material we have imperfectly forgotten. That is why the modern arithmetic book is shorter than Pyke. And if we could but perfectly forget, the modern arithmetic book could grow still shorter.
For instance, Pyke devotes many pages to tables; presumably important tables that he thought the reader ought to be familiar with. His fifth table is labelled ‘'cloth measure.”
Did you know that 24 inches make a “nail?” Well, they do. And 16 nails make a yard, while 12 nails make an ell.
No, wait a while. Those 12 nails (27 inches) make a Flemish ell. It takes 20 nails (45 inches) to make an English ell, and 24 nails (54 inches) to make a French ell. Then, 16 nails plus 15 inches (37 inches) make a Scotch ell.
Now, if you’re going to be in the business world and import and export cloth, you’re going to have to know all those ells — unless you can figure some way of getting the ell out of business.
Furthermore, almost every piece of goods is measured in its own units. You speak of a firkin of butter, a punch of prunes, a fother of lead, a stone of butcher’s meat, and so on. Each of these quantities weighs a certain number of pounds (avoirdupois pounds, but there are also troy pounds and apothecary pounds and so on) and Pike carefully gives all the equivalents.
Do you want to measure distances? Well, how about this: 7 92/100 inches make 1 link; 25 links make 1 pole; 4 poles make 1 chain; 10 chains make 1 furlong; and 8 furlongs make 1 mile.
Or, do you want to measure ale or beer — a very common line of work in Colonial times. You have to know the language, of course. Here it is: 2 pints make a quart and 4 quarts make a gallon.
Well, we still know that much anyway. In Colonial times, however, a mere gallon of beer or ale was but a starter. That was for infants. One had to know how to speak of man-sized quantities. Well, 8 gallons make a firkin — that is, they make “a firkin of ale In London” It takes, however, 9 gallons to make a '‘firkin of beer in London” The intermediate quantity, 8 gallons, is marked down as a '"firkin of ale or beer" — presumably outside of the environs of London where the provincial citizens were less finicky in distinguishing between the two.
But we go on: 2 firkins (I suppose the intermediate kind, but I'm not sure) make a kilderkin and 2 kilderkins make a barrel. Then 15 barrels make 1 hogshead; 2 barrels make a puncheon; and 3 barrels make a butt.
Have you got all that straight?
But let's try dry measure in case your appetite has been sharpened for something still better.
Here, 2 pints make a quart and 2 quarts make a pottle. (No, not bottle, pottle. Don’t tell me you’ve never heard of a pottle!) But let's proceed.
Next, 2 pottles make a gallon, 2 gallons make a peck and 4 pecks make a bushel. (Long breath now.) Then 2 bushels make a strike, 2 strikes make a coom, 2 cooms make a quarter, 4 quarters make a chaldron (though in the demanding city of London, it takes 45 quarters to make a chaldron). Finally, 5 quarters make a wey and 2 weys make a last.”6
Fortunately, the challenges of converting these various regional measures are now consigned to history.
As a student of physics, one of the challenges you encounter in physics deals with converting units. In converting units of measure, you can multiply several fractions together in a process known as dimensional analysis. In dimensional analysis, you create a fraction that equals one, so when it is multiplied by another fraction it does not change the actual measure; instead, it changes to some equivalent measure. The challenge is to decide correctly which fractions to multiply. One process is to decide which unit of measure you wish to replace and to substitute the equivalent measure in the form you desire. This is done so that the undesired unit is cancelled out when multiplied by this equivalent fraction, which leaves the desired unit to take its place.
You can see this process used in the following examples.
EXAMPLE 1.1
If 1 pound (lb) = 16 ounces (oz), how many pounds are in 435 ounces?
435 oz = 435 oz x[latex]\dfrac{1\text{ lb}.}{16\text{ oz}.}[/latex] This operation cancels the oz and leaves the units of lb.
435 oz =[latex]\dfrac{435\text{ lb}}{16\text{ oz.}}[/latex]. Which then reduces to
435 oz = 27 3/16 lb.
The same process can be used to convert problems with several units in them. Consider the following example.
EXAMPLE 1.2
A student averaged 45 miles/hour (mi/h) on a trip. What was the student’s speed in feet/second (ft/s)?
[latex]\dfrac{45 mi}{hr} = 45\text{mi x}\dfrac{5280 ft}{1 mi}\times\dfrac{1 hr}{3600 s}[/latex]
This will cancel the units of mi & hr, and leave ft & s
[latex]45\dfrac{mi}{hr} = 45\times\dfrac{5280\text{ft}}{1 mi}\times\dfrac{1 hr}{3600 s}[/latex]
This then reduces to
45 mi/hr = 66 ft/s
EXAMPLE 1.3
Convert 8 cubic feet (ft3) to cubic yards (yd3)
8 ft3 = 8 ft3 x[latex]\dfrac{1( yd)^{3}}{(3 ft)^{3}}[/latex] This will cancel the units ft3 and replace them with yd3
8 ft3 = 8 ft3 x[latex]\dfrac{1 yd^{3}}{27 ft^{3}}[/latex] Cube the parenthesis
8 ft3 = 8 x[latex]\dfrac{1 yd^{3}}{27}[/latex] Which then reduces to
8 ft3 = 8/27 yd3 (≈ 0.3 yd3)
EXAMPLE 1.4
A room is 10 ft by 12 ft. How many square yards are in the room? The area of the room is 120 square feet (ft2) (Area = Length x Width)
Converting the area yields: 120 ft2 = 120 ft2 x[latex]\dfrac{(1 yd)^{2}}{(3 ft)^{2}}[/latex] Cancel ft2 and replace with yd2
120 ft2 =[latex]\dfrac{120 yd^{2}}{9}[/latex] This then reduces to
120 ft2 = 13 1/3 yd2
The process of dimensional analysis can be used to convert other types of units as well. If we can identify relationships that represent the same value we can make them into a conversion factor
EXAMPLE 1.5
A child is prescribed a dosage of 12 mg of a certain drug per day and is allowed to refill his prescription twice. If there are 60 tablets in a prescription, and each tablet has 4 mg, how many doses are in the 3 prescriptions (original + 2 refills)?
3 Prescriptions = 3 Prescriptions x[latex]\dfrac{\text{60 tablets}}{\text{1 prescription}}\times\dfrac{\text{4 mg}}{\text{1 tablet}}\times\dfrac{\text{1 dosage}}{\text{12 mg}}[/latex]
This cancels all unwanted units
3 Prescriptions =[latex]\dfrac{\text{3 x 60 x 4 x 1}}{\text{1 x 1 x 12}} or\dfrac{720}{12}[/latex] which reduces to
3 Prescriptions = 60 daily dosages
QUESTIONS 1.1 Names and Measurement Terms
Write the corresponding names behind the given unit.
One Dimensional Measures:
mi yd
oz t
mg g
km cm
mm um
ft in
Two Dimensional Measures:
ft2 yd2
m2 cm2
km2 mm2
in2 um2
Three Dimensional Measures:
ft3 yd3
m3 cm3
km3 mm3
in3 um3
QUESTIONS 1.2 Convert the following measures:
- 7 miles (mi) to yards (yd)
- 234 ounces (oz) to short tons (t)
- 11.2 milligrams (mg) to grams (g)
- 1.35 kilograms (km) to centimetres (cm)
- 9 800 000 millimetres (mm) to miles (mi)
- 4.5 square feet (ft2) to square yards (yd2)
- 435 000 square metres (m2) to square kilometrs (km2)
- 8.0 square kilometres (km2) to square feet (ft2)
- 0.0065 cubic kilometres (km3) to cubic metres (m3)
- 14.62 square inches (in2) to square centimetres (cm2)
- 5 500 cubic centimetres (cm3) to cubic yards (yd3)
- 3.5 miles per hour (mi/h or mph) to feet/second (ft/s)
- 185 yards per minute (yd/min) to miles per hour (mi/h or mph)
- 153 feet per second (ft/s) to miles per hour (mi/h or mph)
- 248 miles per hour (mi/h or mph) to metres/second (m/s)
- 186 000 miles per hour (mi/h or mph) to kilometres per year (km/a or km/yr)
- 7.50 tons per square yards (t/yd2) to tons per square inches (t/in2)
- 16 feet per second squared (ft/s2) to kilometres per hour squared (km/h2)
QUESTIONS 1.3.1 Measures of Length
- How many palms are in one league?
- How many points are equal to a poppyseed?

QUESTIONS 1.3.2 Measure of Weight
- Convert your weight in stones. For this you need to research the internet to find which stone conversion to use.
-

English Mass Unit
QUESTIONS 1.3.3 Time Zones
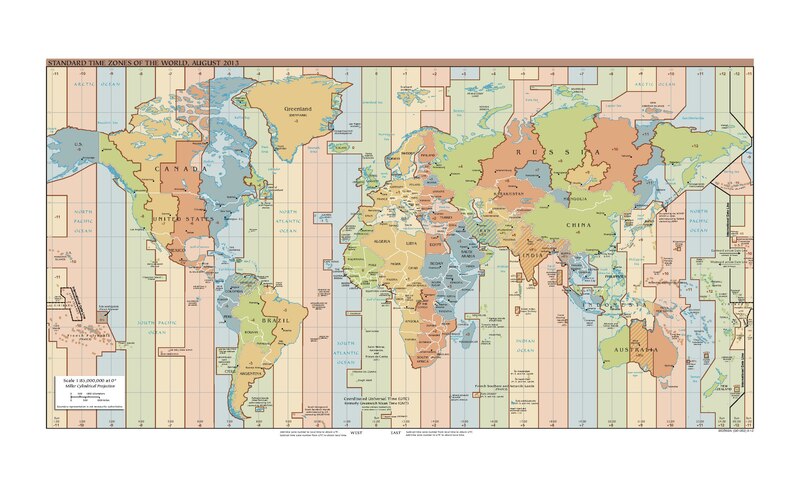
- Using the map below, what is the largest number of time zones you can find for the same latitude?
It is projected that every human is living at least 80 milliseconds in the past....Our observation of actual events takes about this amount of time to process into a cohesive picture:
The passenger steamer SS Warrimoo was quietly knifing its way through the waters of the mid-Pacific on its way from Vancouver to Australia. The navigator had just finished working out a star fix and brought the master, Captain John Phillips, the result. The Warrimoo’s position was latitude 0° 31’ North and longitude 179° 30’ West. The date was 30 December 1899 and it was quickly known that they were only a few miles from the intersection of the Equator and the International Date Line.
Captain Phillips was prankish enough to take full advantage of the opportunity for achieving the navigational freak of a lifetime. He called his navigators to the bridge to check and double check the position of the ship. He changed course slightly to bear directly on his mark. Then he adjusted the engine speed. The calm weather and clear night worked in his favour. At midnight the Warrimoo lay on the Equator at exactly the point where it crossed the International Date Line!
The consequences: The forward part of the ship was in the Southern Hemisphere and the middle of summer, and the stern was in the Northern Hemisphere and the middle of winter. The date in the aft part of the ship was December 31, 1899, while in the forward, it was January 1, 1900. This ship was, therefore, not only in two different days, two different months, two different seasons and two different years but in two different centuries, all at the same time.
Mars Climate Orbiter Mishap Investigation Board Report 10

The Mars Climate Orbiter (MCO) Mission objective was to orbit Mars as the first interplanetary weather satellite and provide a communications relay for the [define acronym] MPL which is due to reach Mars in December 1999. The MCO was launched on December 11, 1998, and was lost sometime following the spacecraft's entry into Mars occultation during the Mars Orbit Insertion (MOI) maneuver. The spacecraft's carrier signal was last seen at approximately 09:04:52 UTC on Thursday, September 23, 1999.
The MCO MIB has determined that the root cause for the loss of the MCO spacecraft was the failure to use metric units in the coding of a ground software file, “Small Forces,” used in trajectory models. Specifically, thruster performance data in English units instead of metric units was used in the software application code titled SM_FORCES (small forces). 11
A file called Angular Momentum Desaturation (AMD) contained the output data from the SM_FORCES software. The data in the AMD file was required to be in metric units per existing software interface documentation, and the trajectory modelers assumed the data was provided in metric units per the requirements.
During the 9-month journey from Earth to Mars, propulsion maneuvers were periodically performed to remove angular momentum buildup in the on-board reaction wheels (flywheels). These Angular Momentum Desaturation (AMD) events occurred 10-14 times more often than was expected by the operations navigation team. This was because the MCO solar array was asymmetrical relative to the spacecraft body as compared to Mars Global Surveyor (MGS) which had symmetrical solar arrays. This asymmetric effect significantly increased the Sun-induced (solar pressure-induced) momentum buildup on the spacecraft. The increased AMD events coupled with the fact that the angular momentum (impulse) data was in English, rather than metric, units, resulted in small errors being introduced in the trajectory estimate over the course of the 9-month journey. At the time of Mars insertion, the spacecraft trajectory was approximately 170 kilometers lower than planned. As a result, MCO either was destroyed in the atmosphere or re-entered heliocentric space after leaving Mars’s atmosphere.
QUESTIONS 1.3.4 Exponential Growth
Sometimes you can run into the challenge of how many times you can fold a piece of paper. The result seems to work out to a maximum of 7 or 8 times, with the wad of paper growing increasingly thicker. Every fold doubles the thickness of the paper being folded. This ends up being an exponential problem where the thickness of the paper being folded can be found from the following equation:
Thickness = (thickness of a single sheet of paper) x 2(number of folds) or simply:
Thickness = (0.0001 m) x 2n
This means ... For n = 1 (1 fold), the thickness is (0.0001 m) x 21 which equals 0.0002 m.
For n = 2 (2 folds), the thickness is (0.0001 m) x 22 which equals 0.0004 m.
For n = 3 (3 folds), the thickness is (0.0001 m) x 23 which equals 0.0008m.
Imagine that you fold the paper once every week for a year (52 folds). The thickness of this folded paper is surprising.
Question:
- How thick would a piece of paper be if it could be folded 52 times?
2. How does this compare to the distance from the Earth to the Sun? (d = 1.496 x 10 11m
Article to read - If you fold a paper in half 103 times it'll get as thick as the universe:
https://gizmodo.com/if-you-fold-a-paper-in-half-103-times-it-will-be-as-thi-1607632639

REFERENCES:
1. Mechanical Universe - Episode 1 Introduction: https://www.youtube.com/watch?v=XtMmeAjQTXc
2. Image is from Vitruvian Man Measurements. Source: https://commons.wikimedia.org/wiki/File:Vitruvian_Man_Measurements.png
3. A-Level Physics Tutor: http://www.a-levelphysicstutor.com/index.php
4. New parts of the brain become active after students learn physics: https://medicalxpress.com/print446393556.html
5. Article to Read - Marvel, K. (2018, June 14) Why I Won’t Debate Science: https://blogs.scientificamerican.com/hot-planet/why-i-wont-debate-science/

