Chapter 14: Mechanical Waves

Equations Introduced for this Topic:
Wave Definition: [latex]T =\dfrac{1}{f}[/latex] Law of Refraction: n1 sin θ1 = n2 sin θ2
Wave Speed:v = λ f Speed of Sound: vair = 331.3 + 0.606 (T - 0°C) m/s
Speed of Ocean Wave:
vocean = a1 + a2 T + a3 T2 + a4 T3 + a5 (S - 35) + a6 dz + a7 dz2 + a8 T (S - 35) + a9 T dz3
Snell’s Law:[latex]\dfrac{\text{sin 01}}{\text{sin 02}} =\dfrac{n_{2}}{n_{1}} =\dfrac{v_{1}}{v_{2}} =\dfrac{λ_{1}}{λ_{2}}[/latex] Law of Reflection: θ1 = θ2
Doppler Shift:[latex]f_{o} =f_{s}\dfrac{(v\underline{+}v_{o})}{(v\underline{+}v_{s})}[/latex] Mach Angle: [latex]sin ø =\dfrac{v_{sound}}{v_{source}} or\dfrac{1}{v_{source}}[/latex]
Where:
T is the period of the wave measured in Seconds (s)
T is the Temperature of the medium the wave is traveling though measured in Celsius (°C)
f is the frequency of the wave motion measured in Hertz (Hz)
fo is the observed frequency of the wave motion measured in Hertz (Hz)
fs is the frequency of the source of the wave motion measured in Hertz (Hz)
v is the velocity of the wave measured in Metres per Second (m/s)
vo is the velocity of the observer moving toward (added) or away (subtracted) from the wave source, measured in Metres per Second (m/s)
vs is the velocity of the wave source moving toward (subtracted) or away (added) from the observer, measured in Metres per Second (m/s)
λ is the wavelength of the wave measured in Metres (m)
θ1and θ2 are the angles of incidence of the wave changing mediums or in reflection
n1and n2 are the indices of refraction of the medium that the wave is traveling through
S is the salinity of the ocean water measured in Parts per Thousand
vsound is the speed of sound given in Metres per Second (m/s) or as a Mach Speed
vsource is the speed of wave source given in Metres per Second (m/s) or as a Mach Speed
Speed of Ocean Wave constants:
| [latex]a_{1} = 1,448.96[/latex] | [latex]a_{2} = 4.591[/latex] | [latex]a_{3} = -5.304\times 10^{-2}[/latex] |
| [latex]a_{4} = 2.374\times 10^{-4}[/latex] | [latex]a_{5} = 1.340[/latex] | [latex]a_{6} = 1.630\times 10^{-2}[/latex] |
| [latex]a_{7} = 1.675\times 10^{-7}[/latex] | [latex]a_{8} = -1.025\times 10^{-2}[/latex] | [latex]a_{9} = -7.139\times 10^{-13}[/latex] |
14.1 Mechanical Wave Motion 2, 3
In this chapter we look at the type of waves that occur in matter; these are classified as mechanical waves. These wave forms are distinguished as being longitudinal and transverse waves. Much of what is covered here is simply an overview of what will be discussed later where the topics and analysis become crucial to understanding specific phenomena.
Historically, the first known recorded studies of wave motion came from the study of the vibrations of strings in musical instruments. The movement of strings in these instruments is up and down (tangential or 90° to the string) and came to be known as “vibratory motion” from the Latin, meaning to shake. The first person known to study the nature of sound waves was Pythagorus of Samos (570-495 BC), who pursued the relationship of the tension on the string being played to the pitch and tone of the sound it emitted when plucked.
Looking at the movement of a string under tension that has been plucked, we can see that it will accelerate under a restoring force towards its equilibrium position (recall Hooke’s Law) until it has passed the equilibrium position where the restorative force then acts to slow the string down to a stop on the opposite side of the equilibrium position. At this point the string then accelerates back under a reduced restoring force, repeating the pattern multiple times before the string has passed through enough frictional forces to dissipate the energy imparted to the string from the initial plucking. It was from these earliest studies into the tension of the string and the tones created that the study of vibratory motion gained the name “simple harmonic motion”4. Hooke’s Law can be applied to the analysis of all instances of the motion of this string. Since this motion repeats itself over and over again, it also gained the name “periodic motion”.
The central concept underlying all mechanical wave motion, specifically the mechanical wave created on any elastic medium that has inertia, is that it can be studied from conservation of energy. Matter in a state of equilibrium can be displaced from that state of equilibrium by applying an external force through some displacement on this medium. This force, through displacement, imparts energy to the medium and as the force is removed from the medium, it then begins to move back to its state of equilibrium, slowly (or rapidly) dissipating energy. This generally creates some type of a wave motion that then moves in directions away from the wave source, dissipating the energy imparted from the initial point of contact. Two types of wave motion: longitudinal and transverse waves, are covered in the following section5.
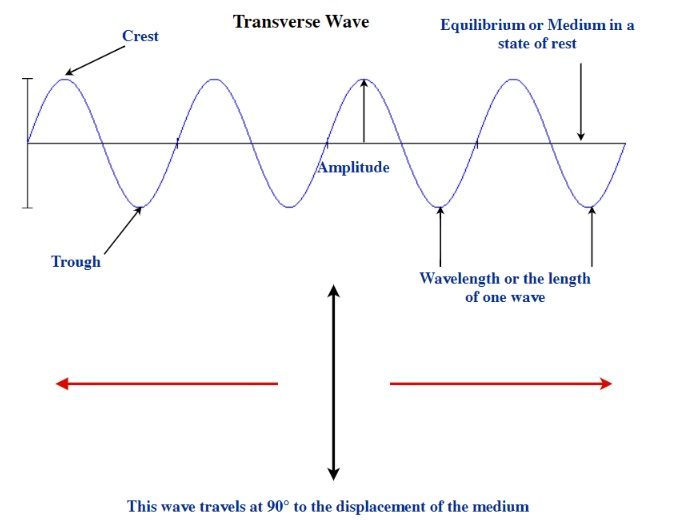
Transverse Waves 6, 7

In transverse waves, the medium moves perpendicularly (90°) to the direction that the wave moves. The most commonly observed wave that has transverse wave properties is that of a water ripple that moves outward from a source of disturbance that acted at some point on the surface of the water. For these types of waves, the water roughly moves in an up and down pattern, which one observes as the waves moving outward. The energy of a transverse wave correlates to the square of the amplitude of the movement of the medium8. This means that if the water surface is displaced 1 metre in causing a transverse wave motion, the energy of the waves that move away from the disturbance are 1/4 the energy carried by waves created if the water surface was displaced by 2 metres. Quantifying this relationship we get:
Energy ∝ Amplitude2
where the amplitude is the measure of the maximum displacement of the medium from its state of rest.
Several terms are associated with transverse waves: 9
• The top of a Transverse wave is called the Crest
• The bottom of a Transverse wave is called the Trough
• The Displacement from the Crest (or Trough) to the equilibrium is the Amplitude
• The Length of a Transverse wave is the Distance between the Crests (or Troughs) is called the Wavelength (λ)
Compressional (or Longitudinal) Waves 10, 11, 12, 13, 14
I FOUND THE PICTURE BUT NOT FREE TO USE ?
Image Source: Settles, Gary "'Seeing the Invisible: The Firing of an AK-47"' Photo, http://www.nytimes.com
Compression waves are caused when an external force displaces particles in a medium away from its state of normal dispersion. This causes the medium to have compressed particles in one region and regions of missing particles (rarefaction) in other regions. As these compressed and rarefaction regions act to stabilize, a wave-type motion occurs. The classic example of this type of a wave motion is sound waves.
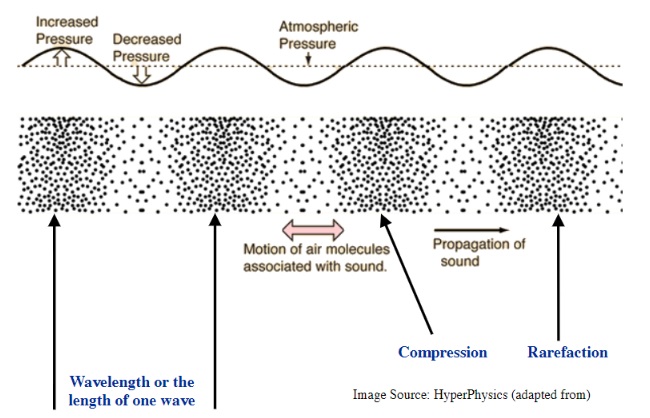
HyperPhysics15 concepts provides an excellent illustration of the compression of air molecules of sound as the sound travels away from some initial disturbance. In this illustration above, some external force would have compressed the air at the left in this image and the resulting disturbance to this medium dissipates away in all directions.
Summarizing these two different types of wave motion:
1. In transverse waves the medium moves tangentially (90°) to the wave motion and in longitudinal waves, the medium moves with and against the motion (0° & 180°) to the wave motion.
2. The energy transported by these waves takes different forms. The energy of the transverse wave relates to the height (amplitude) and amount of medium dislocated from the equilibrium, while the energy of the longitudinal wave is related to the pressure difference of the matter in the medium the wave is traveling through. As such, longitudinal waves have density differences while transverse waves do not.

NOT ABLE TO PUT THIS INTO MEDIA
Energy Transport of a Wave
Calculating the energy of a wave is beyond the scope of this course but is derived from the sum of kinetic and potential energies. Earlier, the total energy of a longitudinal wave was defined by the following relationship: Energy ∝ Amplitude2. While sound energy is also defined as the sum of potential and kinetic energies, variables defining it are based on volume, pressure, particle velocity, densities and the speed of sound. Because of this, one will not encounter generalized algebraic equations for sound energy as for transverse waves above.
14.2 The Speed of Mechanical Waves 16
Equations Introduced:
Wave Definition:[latex]\dfrac{T = 1}{f}[/latex] Wave Speed: v = λ f =[latex]\dfrac{λ}{T}[/latex]
Speed of Sound in air:
vair = 331.3 + 0.606 (T - 0°C) m/s (at 0% Humidity)
Speed of Sound in water:
vocean = a1 + a2 T + a3 T2 + a4 T3 + a5 (S - 35) + a6 dz + a7 dz2 + a8 T (S - 35) + a9 T dz3
where the constants for a are:
| [latex]a_{1} = 1,448.96[/latex] | [latex]a_{2} = 4.591[/latex] | [latex]a_{3} = -5.304\times 10^{-2}[/latex] |
| [latex]a_{4} = 2.374\times 10^{-4}[/latex] | [latex]a_{5} = 1.340[/latex] | [latex]a_{6} = 1.630\times 10^{-2}[/latex] |
| [latex]a_{}7 = 1.675\times 10^{-7}[/latex] | [latex]a_{8} = -1.025\times 10^{-2}[/latex] | [latex]a_{9} = -7.139\times 10^{-13}[/latex] |
Commonly measured properties of wave motion include that of the length of the wave motion (wavelength, given the symbol λ, measured in metres, m), the period of the wave motion given the symbol T, measured in seconds, s and the frequency of the wave-motion, given the symbol f, and measured in Hertz (Hz).
The equation to find the speed of a mechanical wave is defined in exactly the same way as the equation to find average speed, specifically:
[latex]v =\dfrac{d}{t}[/latex] [latex]v =\dfrac{λ}{T}[/latex]
In both cases:
• the speed is measured in metres per second (m/s)
• the distance d and wavelength λ are measured in metres (m)
• the time t and period T are both measured in seconds (s)
While the average speed of a wave can be calculated by its wavelength and period, the factors that influence the speed of the wave passing through the medium include the density, elasticity and temperature of the medium, along with other factors17, 18. These influence wave speed as follows:
Density. The higher the density, the more slowly the wave will travel through it. Sound travels faster in less dense air higher up in the atmosphere than more dense air closer to the surface of the Earth. The temperature is a factor that alters the density of the material. Hot material is less dense than the same material at a colder temperature.
Elasticity. Materials that have a higher elasticity (bulk modulus)19 will have waves that travel faster though lkthem. The bulk modulus is a measure of how much a material will compress under a given amount of external pressure.
Another factor is the speed of the medium the wave is traveling through. This factor is one of relative velocity, specifically the speed of the wave will be ± the speed of the medium the wave is traveling through (if in or opposite to the direction of the wave). If the medium is traveling at an angle to the direction of the wave, trigonometry will be needed to find the relative velocity of the wave (recall Chapter 2.4: Relative Velocity in One Direction).
For this class, we will be calculating the average speed of the wave using wavelength, period and frequency as a general introduction to the study of mechanical wave phenomenon.
Wave Speed: v = λ f =[latex]\dfrac{λ}{T}[/latex]
For more specific measures of the speed of sound in air and water you will use the equations:
Speed of Sound in air:
vair = 331.3 + 0.606 (T - 0°C) m/s (at 0% Humidity) 20
Speed of Sound in water:
vocean = a1 + a2 T + a3 T2 + a4 T3 + a5 (S - 35) + a6 dz + a7 dz2 + a8 T (S - 35) + a9 T dz3
EXAMPLE 14.2.1
While at the White Rock pier, students notice ocean waves rising and falling about 0.5 m every 4.0 s as the tide comes in.
(i) What is the period and frequency of these waves?
T = 4.0 s
f = 1/T
f = 1/4.0 s or 0.25 s-1 (or 0.25 Hz)
(ii) If the crests of the waves are about 10 m apart, what is the speed of the incoming tidal waves?
v = λ f =[latex]\dfrac{λ}{T}[/latex]
v = 10 m (0.25 Hz) or 2.5 m/s
(iii) What is the wavelength of the tidal wave?
λ = 10 m
EXAMPLE 14.2.2
What is the speed of sound on a hot dry day at the ocean if the temperature is 30°C?
vair = 331.3 + 0.606 (T - 0°C) m/s
vair = 331.3 + 0.606 (30°C - 0°C) m/s
vair = 331.3 + 18.2 m/s
vair = 349.5 m/s (≈ 350 m/s)
EXAMPLE 14.2.3
Given the speed of sound in fresh water is around 1481 m/s at 20°C and the speed of sound is 343.21 m/s at the same temperature:
(i) how much time would it take a diver to hear an explosion in the water 2.0 km away?
[latex]v =\dfrac{d}{t}\text{ or t}=\dfrac{d}{v}[/latex]
[latex]t =\dfrac{\text{2000 m}}{\text{1481 m/s}}[/latex]
t = 1.35 s
(ii) How much time would it take to hear the same explosion for an observer standing in a boat above the diver?
[latex]v =\dfrac{d}{t}\text{ or t=}\dfrac{d}{v}[/latex]
[latex]t =\dfrac{\text{2000 m}}{\text{343.21 m/s}}[/latex]
t = 5.83 s
(iii) What is the difference in time between the two people hearing the explosion?
∆t = t air - t water
∆t = 5.83 s - 1.35 s
∆t = 4.48 s
(iv) What are the two wavelengths of the sound in water and in the air?
v = λ f =[latex]\dfrac{λ}{T}[/latex]
λ air ... 343.21 m/s =[latex]\dfrac{λ}{1 Hz}[/latex]
λ = 343.21 m/s ÷ 1 Hz
λ = 343.21 m
λ water ... 1481 m/s =[latex]\dfrac{λ}{1Hz}[/latex]
λ = 1481 m/s ÷ 1 Hz
λ = 1481 m
Mackenzie’s Equation for the Speed of Sound in the Ocean21. The speed of sound in water through solids and liquids is much faster than through the air. The speed of sound in oceans depends on three factors: Temperature (T) in degrees Celsius, the Depth (dz) in Metres and the Salinity of the ocean (S) in parts per thousand. The equation that is used to calculate the speed of sound in the ocean is quite complicated:
vocean = a1 + a2 T + a3 T2 + a4 T3 + a5 (S - 35) + a6 dz + a7 dz2 + a8 T (S - 35) + a9 T dz3
where the constants for “a” are:
| [latex]a_{1} = 1448.96[/latex] | [latex]a_{2} = 4.591[/latex] | [latex]a_{3} = -5.304\times 10^{-2}[/latex] |
| [latex]a_{4} = 2.374\times 10^{-4}[/latex] | [latex]a_{5} = 1.340[/latex] | [latex]a_{6} = 1.630\times 10^{-2}[/latex] |
| [latex]a_{7} = 1.675\times 10^{-7}[/latex] | [latex]a_{8} = -1.025\times 10^{-2}[/latex] | [latex]a^{9} = -7.139\times 10^{-13}[/latex] |
EXAMPLE 14.2.4
What is the speed of sound 1000 m below the ocean’s surface, where the temperature is 6.2 °C and the salinity is 4 parts per thousand?
| [latex]v_{ocean} = a_{1}[/latex] | [latex]v_{ocean} = 1448.96[/latex] | [latex]v_{ocean} = 1448.96[/latex] |
| [latex]+ a_{2} T[/latex] | [latex]+ 4.591 (6.2)[/latex] | [latex]+ 28.46[/latex] |
| [latex]+ a_{3} T_{2}[/latex] | [latex]- 5.304\times 10^{-2} (6.2)^{2}[/latex] | [latex]- 2.04[/latex] |
| [latex]+ a_{4} T_{3}[/latex] | [latex]+ 2.374\times 10^{-4} (6.2)^{3}[/latex] | [latex]+ 0.06[/latex] |
| [latex]+ a_{5} (S - 35)[/latex] | [latex]+ 1.340 (4 - 35)[/latex] | [latex]- 41.54[/latex] |
| [latex]+ a_{6} d_{z}[/latex] | [latex]+ 1.630\times 10^{-2} (1000)[/latex] | [latex]+ 16.30[/latex] |
| [latex]+ a_{7} dz_{2}[/latex] | [latex]+ 1.675\times 10^{-7} (1000)^{2}[/latex] | [latex]+ 0.17[/latex] |
| [latex]+ a_{8} T (S - 35)[/latex] | [latex]- 1.025\times10^{-2} (6.2)(4 - 35)[/latex] | [latex]+ 1.97[/latex] |
| [latex]+ a_{9} T dz_{3}[/latex] | [latex]- 7.139\times 10^{-13} (6.2)(1000)^{3}[/latex] | [latex]- 0.00[/latex] |
vocean = 1.448.96
QUESTIONS 14.2 The Speed of Mechanical Waves
14.3 Wave Properties - Reflection, Refraction, Interference and Diffraction 22
Reflection:
Reflection, Refraction and Diffraction are all common properties of a wave motion that occur when a wave meets a barrier, changes speed or encounters an obstacle in its path of motion. Each one of these disruptions will manifest changes to the wave itself, which can be quantified, allowing one to measure the predicted change.
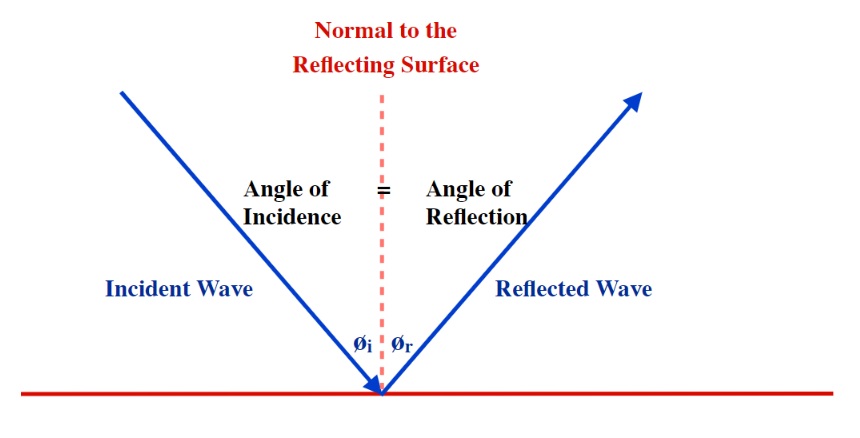
The first of these, the Law of Reflection, occurs when a wave front encounters a smooth reflecting surface and the angle the wave strikes the surface equals the angle at which the wave is reflected. For this phenomenon:
Angle of Incidence = Angle of Reflection
or
øincidence = øreflection
which is often shortened to
øi = ør
The angles for this law are measured from the normal 23 of the wave striking the surface. In a diagram, this looks as follows:
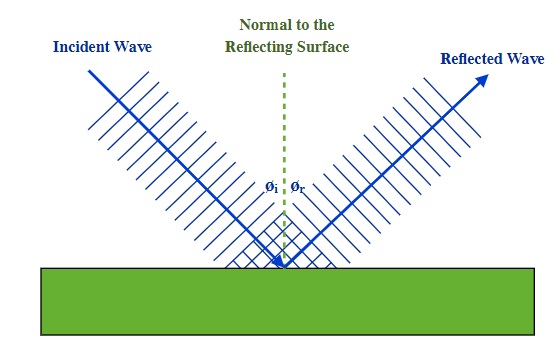
Often one encounters an image, as follows, that is used to illustrate a series of wave-crests reflecting off a surface.
More often, a wave will encounter and reflect off an uneven or a rough surface. For these instances, the wave reflection is classified as a diffuse reflection where the reflected waves are scattered in many directions.
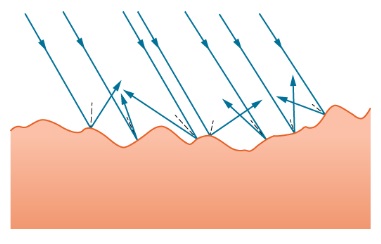
These waves will still reflect off the surface, obeying the law of reflection, however as you can see, the inclination of the reflecting surface changes, which results in the wave being scattered in multiple directions.
(Image Source: LibreTexts, UC Davis)
Of special interest to musicians and others is the nature of the reflection from a boundary24, whether it be a fixed or an open boundary. The difference in these reflections is behind the nature of musical instruments.
Fixed Boundary
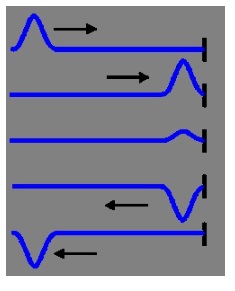 If a wave form is reflected back from a fixed end, then the wave inverts itself 180°. If it enters as a crest it reflects as a trough, or the reverse of this. This type of reflection is what is observed on stringed instruments and is responsible for a phenomenon called resonance; it is what strings produce as a certain note when struck. Only waves of a certain wavelength and frequency will result due to this reflection and the constructive and destructive interference that results. If not for this interference from the wave reflection, the music produced would be a jumble of notes. When covered in more detail, this will be described as a standing wave pattern. This was a phenomenon that was crucial in the early developments of understanding the movement of electrons surrounding the nucleus of the atom.
If a wave form is reflected back from a fixed end, then the wave inverts itself 180°. If it enters as a crest it reflects as a trough, or the reverse of this. This type of reflection is what is observed on stringed instruments and is responsible for a phenomenon called resonance; it is what strings produce as a certain note when struck. Only waves of a certain wavelength and frequency will result due to this reflection and the constructive and destructive interference that results. If not for this interference from the wave reflection, the music produced would be a jumble of notes. When covered in more detail, this will be described as a standing wave pattern. This was a phenomenon that was crucial in the early developments of understanding the movement of electrons surrounding the nucleus of the atom.
Open Boundary
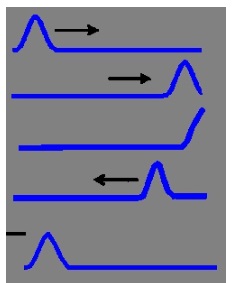 If a wave form is reflected back from an open end, then the wave reflects back on itself, having no phase change. If it enters as a crest it reflects as a crest, or if at a trough it reflects as a trough. This type of reflection is what is observed on pipe instruments (flutes - tubas) and is also responsible for the resonance that these instruments produce as a certain note from air moving past the openings. As with the stringed instruments, only waves of a certain wavelength and frequency will result, due to this reflection and the constructive and destructive interference that results. Also, if not for this interference from the wave reflection, the music produced would be a jumble of notes.
If a wave form is reflected back from an open end, then the wave reflects back on itself, having no phase change. If it enters as a crest it reflects as a crest, or if at a trough it reflects as a trough. This type of reflection is what is observed on pipe instruments (flutes - tubas) and is also responsible for the resonance that these instruments produce as a certain note from air moving past the openings. As with the stringed instruments, only waves of a certain wavelength and frequency will result, due to this reflection and the constructive and destructive interference that results. Also, if not for this interference from the wave reflection, the music produced would be a jumble of notes.
(Image Source: pngkit.com)
The Interference of Waves25 is another phenomenon that has had major implications in understanding the nature of light, quantum mechanics and relativity. Wave interference is where waves meet together on the same medium with the result ranging from combining constructively or destructively.
Constructive interference occurs when waves meet in phase and combine to make a bigger wave. This phenomenon is a classic feature of many open ocean disaster movies that involve Rogue Waves 26 (a.k.a. monster waves, killer waves, etc.), where waves meet and combine on open water as a result of high winds and strong currents. These waves have been responsible for maritime disasters and are credited with numerous ships lost at sea 27. These waves have also been known to strike land, as in Florida, July 1992, where hundreds of vehicles were damaged and 75 people injured, or California, Spain and South Korea, with fatalities occurring at each of these locations.
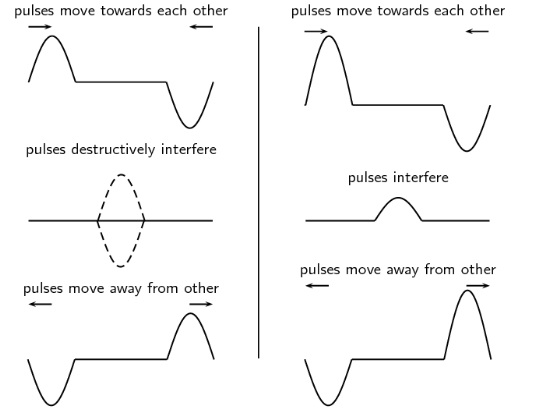
Destructive interference28 is the exact opposite, and occurs when waves meet to cancel each other out. The meeting of these two waves is sometimes known as superposition, where the amplitudes of the two waves are added to or subtracted from each other.
Standing, traveling waves, nodes and antinodes are all part of the physics of interferenceand resonance. While not covered in this chapter, in your later physics courses you will be covering these, as they are important phenomena to help you understand any number of different events in our world.
Diffraction
Diffraction is the last of wave phenomenon to be covered in this chapter that has important ramifications in understanding the nature of matter. Diffraction is the ability of waves to bend around corners, objects and through openings. Wave diffraction is a common phenomenon and is observed on a daily basis, such as hearing sounds from around a corner or if behind a dock or near a pier; water waves rise and fall as waves pass by, albeit at a reduced amplitude. The ability of water waves to bend around objects occurs when the wavelengths are larger than the objects they encounter. When the wavelengths of the wave are smaller than the objects they encounter, the amount of diffraction is significantly reduced.
Interference patterns from two wave sources29 are of special interest to physicists due to experiments by scientists studying the wave nature of light and slow moving electrons passing through a laboratory experiment using diffraction gratings. Looking at the interference patterns resulting from waves passing (diffracting) through two openings and observing the results on a screen set a distance back from the two openings is central to understanding these results.
What results is a series of constructive and destructive interference patterns on the screen.
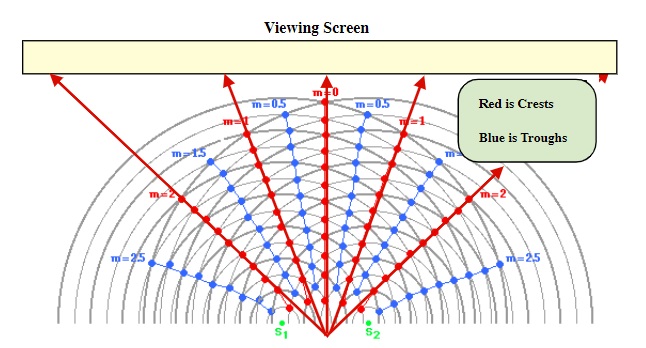
The red arrows show the pathways of constructive interference and indicate where the maximum of any wave motion occurs. If placed, blue arrows tracing the maximum destructive interference would create a similar pattern of interference that would be placed between the maximum constructive interference spots.
The following equation is useful in positioning the maximum constructive and destructive interference patterns on the viewing screen.
[latex]λ =\dfrac{x d}{m L}[/latex]
Where
λ is the length of the wave that is coming from these two openings or sources
x is the distance between the constructive (or destructive) interference patterns on the screen
d is the distance separating the two sources of waves
L is the distance from the two wave sources to the viewing screen
n is the count number of constructive (1, 2, 3, 4, ...) or destructive (0.5, 1.5, 2.5, 3.5...) interference patterns from the very central constructive interference pattern on the view screen.
The previous equations are illuminated in the following examples.
EXAMPLE 14.3.1
Suppose you have two wave generators producing waves on a wave tank where the speed of the waves created is 1.2 m/s. If these waves have a frequency of 18.0 Hz, find:
(i) What is the wavelength and period of the waves that are created?
v = 1.2 m/s v = λ f
f = 6.0 Hz λ = v ÷ f
λ = find λ = 1.2 m/s ÷ 18.0 Hz or 0.067 m
T = find [latex]T =\dfrac{1}{f}[/latex]
[latex]T =\dfrac{1}{\text{18 Hz}}[/latex]
T = 0.056 s
(ii) If these wave generators are 25 cm apart and 0.42 m away from a viewing screen, what distance separates the central constructive interference pattern from the next constructive interference pattern?
[latex]λ =\dfrac{x d}{n L}[/latex]
Isolating for x ...
[latex]x =\dfrac{\text{λ nL}}{d}[/latex]
[latex]x =\dfrac{(0.067 m)(1)(\text{0.42 m})}{(\text{0.25 m})}[/latex]
x = 0.093 m or 9.3 cm
(iii) If these wave generators are creating interference patterns on a 0.80 m viewing screen, how many constructive interference patterns can be observed on this screen?
We start this solution by looking at the distance to the edge of the viewing screen from the central constructive interference pattern. This is the maximum value of x.
x max = 0.80 m ÷ 2 or 0.40 m of viewing screen on either side
Now we solve for n using the value for x max
λ = x d
n L
Isolating for n
n = x d
λ L
n = (0.40 m)(0.25 m)
(0.0667 m)(0.42 m)
n = 3.57
This means that 3 full constructive interference patterns will be seen on either side of the central constructive interference pattern.
Looking at the geometry of the interference pattern from two separate coherent wave sources, we can rewrite the equation
[latex]λ =\dfrac{x d}{n L}[/latex]
as
d sin ø = n λ
This is done as follows:
For this geometry to be solved, the distance L to the viewing screen must be quite large in comparison to the distance between the two wave sources. This will allow the three angles measuring ø to be very close in value to each other.
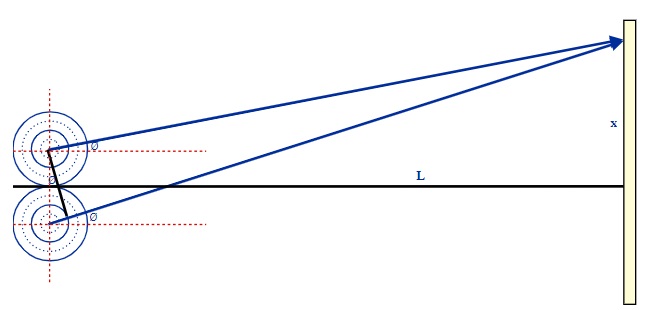
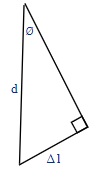 If we expand the small triangle at the source at the two wave generators, we get
If we expand the small triangle at the source at the two wave generators, we get
From this we can see that sin ø =[latex]\dfrac{\Delta{l}}{d}[/latex]
Also, ∆ l = n λ because ∆ l in length is equal to 1, 2, 3, or more complete
wavelengths.
Combining the above, we get our equation d sin ø = n λ
These two equations λ = [latex]\dfrac{x d}{n L}[/latex] and d sin ø = n λ
allow one to estimate both the angle separating constructive and destructive interference from two coherent wave sources and the distance between the interference patterns on a viewing screen. The condition for this equation to be valid is that L >> d.
The value of the mechanics of constructive and destructive interference patterns is crucial to understanding both the nature of light and matter.
EXAMPLE 14.3.2
If you have two coherent wave sources 28 cm apart that are emitting waves of length 3.0 cm, find:
(i) At what angle would one find the first and second constructive wave interference patterns from the direction where the waves are headed?
From d sin ø = n λ we isolate ø to yield ø = sin-1 (n λ ÷ d)
Data
d = 0.28 m ø1 = sin-1 [(1)(0.030 m) ÷ 0.28 m]
λ = 0.030 m ø1 = 6.2°
n = 1, 2 ø1 = sin-1 [(2)(0.030 m) ÷ 0.28 m]
ø = find ø1 = 12.4° (≈ 12°)
(ii) What distance separates these two constructive wave patterns on a viewing screen that is 0.84 m away from the wave sources?
Data
d = 0.28 m x1 =[latex]\dfrac{λ n L}{d}[/latex] x2 =[latex]\dfrac{λ n L}{d}[/latex]
λ = 0.030 m
[latex]x_{1} =\dfrac{(\text{0.030 m})(1)(\text{0.84 m})}{\text{0.28 m}}[/latex] [latex]x_{2} =\dfrac{(\text{0.030 m})(2)(\text{0.84 m})}{\text{0.28 m}}[/latex]
n = 1, 2
x = find x1 = 0.090 m x2 = 0.18 m
L = 0.84 m
∆x = x2 - x1 or 0.18 m - 0.090 m = 0.090 m
Refraction is a phenomenon that occurs when a wave travels from one medium to another and changes its speed and wavelength due to changes in the medium it is traveling through. One common feature is that the wave can change in direction, which can be observed if it encounters a change in medium at an angle other than 0°. If you have ever experienced trying to use a stick to touch an object that is under water, you will have noticed the distortion between what you see and what is actually happening.
There are three possible outcomes where a wave speeds up as it leaves one medium to another: refraction, refraction at a critical angle along the boundary of the medium, and total internal reflection. In all cases, the outcome can be predicted using Snell’s Law.
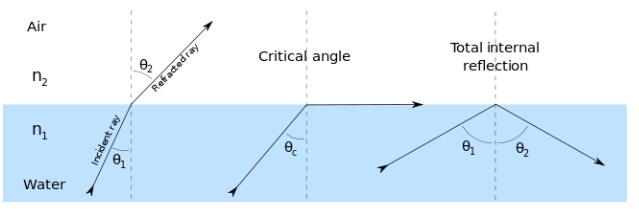
Snell’s Law has the legacy of being discovered, lost and unpublished by many early scientists and natural philosophers. The first of these was Ptolemy of Alexandria (100-170 AD), whose work had inaccuracies at small angles, and later by Ibn Sahl (940-1000 BC), who used this law to create an optical lens with no geometric aberrations. Thomas Harriot (1560-1621) was the first to discover Snell’s Law (but did not publish his results) as did Willebrord Snell in his study of light (he also did not publish his results). This came to be known as Snell’s Law due to the writing of Christian Huygens, who identified Snell as the original author of this finding in his 1678 work Traité de la Lumière.
Snell’s Law is often reduced to
Law of Refraction: n1 sin θ1 = n2 sin θ2
The variables in this equation that are useful to expand Snell’s Law are:
θ1 & θ2 are the incident and refracted angles of the wave as it travels from one medium to the other.
n1 & n2 are the indices of refraction of the two medium, which have since come to be defined as the speed of light divided by the speed in the medium.
Index of Refraction [latex]n =\dfrac{c}{v}[/latex]
v1 & v2 are the incident and refracted speeds of the wave in these different media.
λ2 & λ2 are the incident and refracted wavelengths of the wave in these different media.
Snell’s Law is therefore expanded using the relationship of
Wave Speed: v = λ f =[latex]{λ}{T}[/latex]
To become its final form of
Snell's Law: [latex]\dfrac{\text{sin 0}_{1}}{\text{sin 0}_{2}} =\dfrac{n_{2}}{n_{1}} =\dfrac{v_{1}}{v_{2}} =\dfrac{λ_{1}}{λ{2}}[/latex]
While Snell’s Law directly stems from the study of light waves, this chapter deals only with mechanical waves that travel on or in matter, and there is no refractive index for mechanical waves. As such, Snell’s Law, when applied to mechanical waves, reduces to
Snell's Law: [latex]\dfrac{\text{sin 0}_{1}}{\text{sin 0}_{2} =\dfrac{v_{1}}{v_{2}} =\dfrac{λ_{1}}{λ_{2}}[/latex]
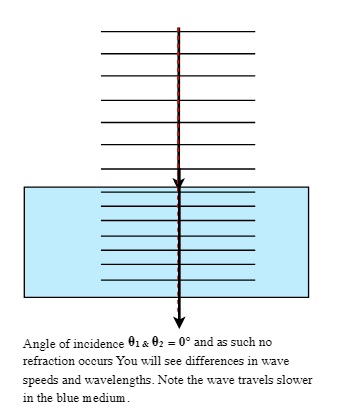
In the following illustration, waves pass from a fast to a slower medium. If the angle of incidence is at 0° from the normal, the wave will continue at straight ahead. The only change is to its wavelength and wave speed. The frequency remains the same and the wave does not change direction.
If the angle of incidence is at an angle greater than 0°, then not only the wavelength and wave speed, but also the direction that the wave is traveling, change. As the wave slows down it will bend towards the normal. Only the frequency remains constant.
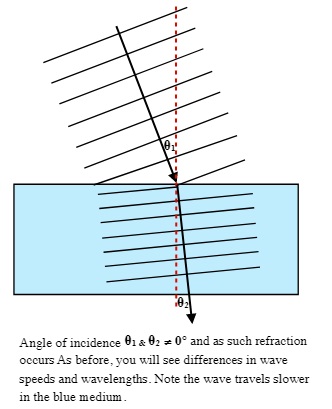
In the reverse of this, where a wave travels from a slow to a fast medium, the wavelength and speed increase. If the angle of travel is the same as the direction of the normal, then the wave does not change direction and keeps going straight. If, however, the wave is traveling at an angle to the normal, then the wave speeds up and bends away from the normal. These are the three situations that are possible, and were illustrated earlier.
The following examples illustrate these possibilities.
EXAMPLE 14.3.3
Suppose you have a wave front of 4.2 m wavelength traveling 0.51 m/s that enters a medium where the wave speeds up to 0.64 m/s. If this wave is angled at 48° to the normal and part of the wave is reflected and the rest of it refracted, find the following:
(i) What are the wavelengths of the reflected and refracted waves?
λ reflected is unchanged at 4.2 m
λ refracted is found by using part of the extended version of Snell’s Law:
Data:
v1 = 0.50 m/s [latex]\dfrac{v_{1}}{v_{2}} =\dfrac{λ_{1}}{λ_{2}}[/latex]
λ1 = 4.2 m
[latex]\dfrac{λ_{2}}{v_{1}} = v_{2}λ_{1}[/latex]
v2 = 0.64 m/s
λ2 = find [latex]λ_{2} =\dfrac{(\text{0.64 m/s})(\text{4.2 m})}{\text{0.51 m/s}}[/latex]
λ2 = 5.27 m (≈ 5.3 m)
(ii) What are the angles of the reflected and refracted waves?
ø reflected is unchanged at 48°
ø refracted is found by using Snell’s Law:
Data:
v1 = 0.50 m/s [latex]\dfrac{\text{sin 0}_{1}}{\text{sin 0}_{2}} =\dfrac{v_{1}}{v_{2}}[/latex]
ø1 = 48°
v2 = 0.64 m/s [latex]sin\phantom{0}0_{2}=\dfrac{v_{2}\phantom{0}sin 0_{1}}{v_{1}}[/latex]
ø2 = find
[latex]\text{sin 0}_{2} =\dfrac{\text{0.64 m/s sin }48°}{\text{0.51 m/s}}[/latex]
in θ2 = 0.9326
θ2 = sin-1 0.9326
θ2 = 68.8° (≈ 69°)
(iii) At what incident angle would this wave front be completely reflected, with no refraction?
Data:
v1 = 0.50 m/s [latex]\dfrac{sin\phantom{0}0_{c}}{sin\phantom{0}0_{2}}=\dfrac{v_{1}}{v_{2}}[/latex]
øc = find
v2 = 0.64 m/s sin 0c =[latex]\dfrac{v_{1} sin 0_{2}}{v_{2}}[/latex]
ø2 = 90°
sin 0c =[latex]\dfrac{\text{0.50 m/s sin} 90°}{\text{0.64 m/s}}[/latex]
sin θc = 0.7969
θc = sin-1 0.7969
θc = 52.8° (≈ 53°)
QUESTIONS 14.3 Wave Properties - Reflection, Refraction, Interference and Diffraction
1. Suppose you have two wave generators producing on a wave tank where the speed of the waves created are 1.4 m/s. If these waves have a frequency of 24.0 Hz, find:
(i) What is the wavelength and period of the waves that are created?
(ii) If these wave generators are 18 cm apart and are 0.64 m away from a viewing screen, what distance separates the central constructive interference pattern from the next constructive interference pattern?
(iii) If these wave generators are creating interference patterns on a 0.96 m viewing screen, how many constructive interference patterns can be observed on this screen?
2. How many constructive interference patterns will one be able to observe on a viewing screen under the following criteria: The waves are traveling at 0.84 m/s, have a frequency of 20 Hz, are created by two wave generators 18 cm apart, and are at a distance of 0.60 m away from a viewing screen that is 1.0 m in length.
3. If you have two coherent wave sources 24 cm apart that are emitting waves of length 4.2 cm, find:
(i) At what angle would one find the second and third constructive wave interference patterns from the direction where the waves are headed?
(ii) What distance separates these two constructive wave patterns on a viewing screen that is 0.60 m away from the wave sources?
4. What angle would separate the central constructive interference pattern and the fourth constructive interference pattern for two coherent wave generators separated by 12 cm that are generating waves 3.6 cm in length?
5. Suppose you have a wavefront of 2.2 m wavelength traveling at 0.48 m/s that enters a medium where the wave speeds up to 0.84 m/s. If this wave is angled at 28° to the normal and part of the wave is reflected and the rest of it refracted, find the following:
(i) What are the wavelengths of the reflected and refracted waves?
(ii) What are the angles of the reflected and refracted waves?
(iii) At what incident angle would this wave front be completely reflected, with no refraction?
6. What is the critical angle for a wavefront of 1.6 m wavelength traveling at 0.50 m/s that enters a medium where the wave speeds up to 0.75 m/s. (The critical angle is where the wave does not refract but instead reflects.)
14.4 The Doppler Effect30 and Shock Waves

Equations Introduced:
Doppler Shift: [latex]f_{o} = f_{s}\dfrac{(v\underline{+}v_{o})}{v\underline{+}v_{s}}[/latex] Mach Angle: sin ø =[latex]\dfrac{v_{sound}}{v_{source}} or\dfrac{1}{v_{source}}[/latex]
Where:
fo is the observed frequency of the wave motion measured in Hertz (Hz)
fs is the frequency of the source of the wave motion measured in Hertz (Hz)
v is the velocity of the wave measured in Metres per Second (m/s)
vo is the velocity of the observer moving toward (added) or away (subtracted) from the wave source, measured in Metres per Second (m/s)
vs is the velocity of the wave source moving toward (subtracted) or away from (added) the observer, measured in Metres per Second (m/s)
vsound is the speed of sound given in Metres per Second (m/s) or as a Mach Speed
vsource is the speed of wave source given in Metres per Second (m/s) or as a Mach Speed

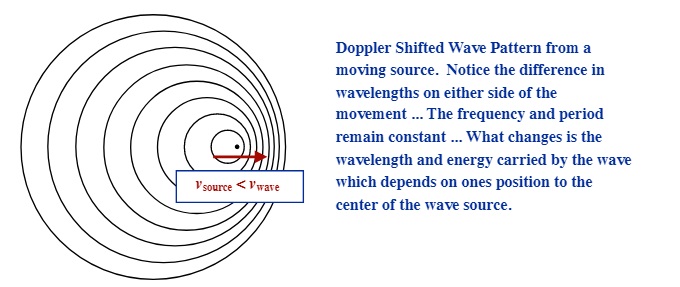
The Doppler effect31 is a common feature of all wave motion (sound, water, light, gravity) if either the source or the observer are moving with respect to each other. While this topic only covers mechanical waves as found in sound and water, the topic of Doppler shifts for light and gravity will be revisited in the course that follows this one.
The Doppler effect is named after its discoverer, Christian Doppler, who, a year into starting work at Prague Polytechnic in Czechoslovakia, discovered that the measured frequency of both sound and light waves could be altered by the motion of either the source or the observer moving towards each other. This was published in 1842 as "Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels"32. While Doppler originally used his theory to explain the astronomical observation of the varying colours of binary stars, Buys Ballot (1845) confirmed that sound waves experienced Doppler shifts. Hippolyte Fizeau independently discovered the Doppler effect for electromagnetic waves six years later in 1842.
The Doppler Shift phenomenon occurs when the source of a wave is moving either towards or away from an observer and/or if the observer is moving towards or away from a wave source. We commonly experience this when we are listening to the sound of a siren from an emergency vehicle that is moving either towards or away from us. The shift in sound frequency (we hear this as the pitch of the sound we hear) is most pronounced if we hear the sound of high speed vehicles such as a race car33, airplane34 or jet35 in motion near us. We should note that the frequency of the sound does not change, rather it is how we hear the sound as altered by the relative motion between the source or the observer. The source puts out the same frequency; the observer perceives a different frequency. Doppler shifts are therefore the shift in observed frequency and not a change in the actual frequency of the source. The equation we use to measure the change in frequency is as follows:
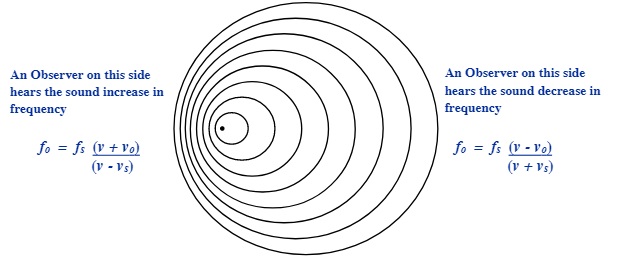
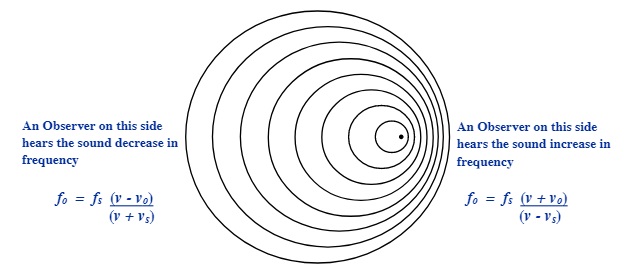
When the observer is moving towards the source or if the source is moving towards the observer, the sound waves increase in frequency. For these cases the equation shows this as:
fo = fs (v + vo) Add the velocity of the observer
(v - vs) Subtract the velocity of the source
When the observer is moving away from the source or if the source is moving away from the observer, the sound waves decrease in frequency. The equation shows this as:
fo = fs (v - vo) Subtract the velocity of the observer
(v + vs) Add the velocity of the source
The above relationship is shown in the following two diagrams:
Alarms and sirens generally emit sound with frequencies in the 1000 Hz to 3000 Hz (1-3 kHz) range, as this is the range that humans are most sensitive to hearing36. Since this is a common sound that one can experience, the following examples will deal with these frequencies.
EXAMPLE 14.4.1
What is the wavelength of a 1.5 kHz siren where sound travels at 343 m/s?
Data:
v = 343 m/s v = λ f or λ = v ÷ f
λ = find λ = 343 m/s ÷ 1500 Hz
f = 1.5 kHz λ = 0.229 m (≈ 0.23 m)
EXAMPLE 14.4.2
If an ambulance is racing past you at 140 km/h on a freeway beside a path you are walking on, what frequencies do you hear as (i) the ambulance approaches you and (ii) as the ambulance moves away from you? Assume the siren is emitting a frequency of 2000 Hz and the speed of sound on that day is 340 m/s.
First 140 km/h ÷ 3.6 = 38.9 m/s
Data
fo = find
fs = 2000 Hz
v = 340 m/s Use [latex]f_{o} = f_{s}\dfrac{(v\underline{+} v_{o})}{(v\underline{+}v_{s})}[/latex]
vo ≈ 0 m/s (insignificant)
vs = ± 38.9 m/s (Towards - 38.9 m/s, Moves Away + 38.9 m/s)
(i) Approaches
fo = 2000 Hz[latex]\dfrac{(\text{340 m/s + 0 m/s})}{(\text{340 m/s - 38.9 m/s})}[/latex]
fo = 2258 Hz (≈ 2300 Hz)
(ii) Moves away
fo = 2000 Hz[latex]\dfrac{(\text{340 m/s + 0 m/s})}{(\text{340 m/s + 38.9 m/s})}[/latex]
fo = 1795 Hz (≈ 1800 Hz)
EXAMPLE 14.4.3
If you are driving in the opposite lane at 110 km/h and hear the same ambulance described in Example 14.4.2, what frequencies do you hear as:
(i) the ambulance approaches you
(ii) the ambulance moves away from you?
Assume the siren is emitting a frequency of 2000 Hz.
First 140 km/h ÷ 3.6 = 38.9 m/s and 110 km/h ÷ 3.6 = 30.6 m/s
Data:
fo = find
fs = 2000 Hz
v = 340 m/s Use fo = fs [latex]\dfrac{(v\underline{+}v_{o})}{(v\underline{+}v_{s})}[/latex]
vo ≈ 0 m/s (insignificant)
vs = 30.6 m/s ± 38.9 m/s
(Towards 30.6 m/s & - 38.9 m/s, Moves Away - 30.6 m/s & + 38.9 m/s)
(i) Approaches
fo = 2000 Hz[latex]\dfrac{(\text{340 m/s + 30.6 m/s})}{(\text{340 m/s - 38.9 m/s})}[/latex]
fo = 2462 Hz (≈ 2400 Hz)
(ii) Moves away
fo = 2000 Hz[latex]\dfrac{(\text{340 m/s - 30.6 m/s})}{(\text{340 m/s + 38.9 m/s})}[/latex]
fo = 1633 Hz (≈ 1600 Hz)
QUESTIONS 14.4 The Doppler Effect and Shock Waves
1. What is the frequency of a sound that has a wavelength of 0.25 m where sound travels at 332 m/s?
2. An ambulance is racing down a road at 70 km/h and hits the horn to warn vehicles in the intersection that it is approaching. At this instant there are 4 observers in all four directions, each at 200 m away from the ambulance. Who hears the sound of the horn first?
3. If a firetruck is racing past you at 110 km/h on a freeway beside a path you are walking on, what frequencies do you hear as
(i) the firetruck approaches you; and
(ii) as the firetruck moves away from you? Assume the siren is emitting a frequency of 1200 Hz and the speed of sound on that day was 340 m/s.
4. If you are driving in the opposite lane at 90 km/h and hear the same firetruck described in the previous question, what frequencies do you hear as
(i) the firetruck approaches you; and
(ii) as the firetruck moves away from you? Assume the siren is emitting a frequency of 1200 Hz.
5. If you are driving on a freeway at 90 km/h and a police car is approaching from behind at 160 km/h, emitting a siren with a varying frequency from 1-3 kHz, what range of frequencies would you hear in your car?
Shock Waves and Sonic Booms
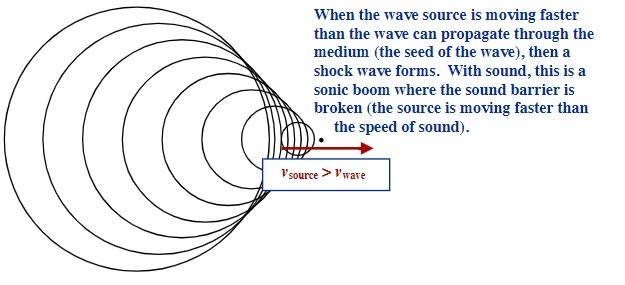
When objects move more slowly than the speed of the wave in a medium, then Doppler shifts can be observed. When objects move at or greater than the speed of the wave in that medium then a shock wave will result. The most common of shock waves are that of a sonic boom (when the object travels faster than the speed of sound) and of the bow waves off a moving object on the surface of water. While similar to look at, the common V-shape of a flock of migratory birds relates to air turbulence created by the leading bird. The lead bird pushes the air down from its wings during a flap and to either side; this air pushes upward, making it easier for the birds behind the leader to fly. Migrating birds will take turns flying in the lead since this is the hardest position to fly in.
Sonic booms or shock waves are common with most munitions, where speeds range as high as Mach 3 (3 times the speed of sound), but present a challenge for aircraft to travel faster than sound. As aircraft improved in speeds attained throughout WWII, damage to the aircraft causing it to crash became almost certain at a speed of 85% of the speed of sound (Mach 0.85). The first aircraft on record to officially to break the sound barrier was the Bell X-1, flown by Chuck Yeager in 1948. Within a few years, aerodynamic design on jet aircraft had improved so much that aircraft routinely broke the sound barrier.
What is covered in the remainder of this chapter is the physics of the shock wave produced by flying at or greater than the speed of sound.
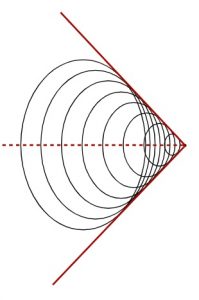
The Mach Angle of Sonic Booms
When the source of a wave motion is traveling faster than the wave can travel in a medium, a shock wave is formed. In water, it is common to see the shock wave formed as a v-shape as the boat moves through the water.
For any airborne object the shockwave only occurs when the object is traveling faster than the speed of sound or vsource > mach 1.
For airborne objects, the angle formed is called the Mach Angle 37. While NASA defines this angle as µ, a number of physics textbooks use a regular Greek symbol to represent the angle ø.
This angle is measured from the center of the cone formed by the shockwave to the outside edge of the shockwave and is defined by the relationship:
sin ø =[latex]\dfrac{v_{Sound}}{v_{source}}[/latex] which can be shortened to [latex]\text{sin ø} =\dfrac{1}{v_{source}}[/latex] where 1 stands for Mach 1
and vsource is given in terms of Mach.
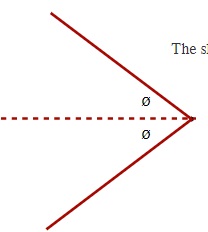
The sketch to the left shows how to measure the Mach angle.
EXAMPLE 14.4.5
What is the speed of a jet (given as a Mach speed), that is producing a Mach angle cone of 42°?
Data:
ø = 42°
v jet = find
v sound = Mach 1
[latex]\text{sin ø} =\dfrac{v_{sound}}{v_{jet}} or\dfrac{1}{v_{jet}}[/latex]
[latex]\text{sin 42°} =\dfrac{Mach 1}{\text{sin 42°}}\text{or v}_{jet} =\dfrac{\text{Mach 1}}{\text{sin 42°}}[/latex]
v jet = Mach 1.49 (≈ Mach 1.5)
EXAMPLE 14.4.6
What amount of time would it take the shockwave (Mach angle cone) to reach an observer 400 m below on the ground if the jet producing the shockwave is traveling at 2300 km/h?
First, 2300 km/h ÷ 3.6 = 639 m/s
Since the jet speed of 639 m/s is much greater than the speed of sound, the observer would first hear the jet as it flew directly over top.
Therefore, this becomes a simple constant speed question
Data:
v = 350 m/s (≈ 31°C) [latex]v =\dfrac{d}{t} or\dfrac{d}{v}[/latex]
d = 400 m
t = find [latex]t =\dfrac{\text{400 m}}{\text{350 m/s}}[/latex] or 1.14 s ( ≈ 1.1 s)
EXAMPLE 14.4.7
A jet traveling at Mach 1.8 flies overhead of an observer 500 m below. By the time the shockwave reaches the observer, how far horizontally has this jet traveled?
As above, since the jet speed of 630 m/s is much greater than the speed of sound, the observer would first hear the jet as it flew directly overhead.
Data for the sound to reach the observer:
v = 350 m/s (≈ 31°C) [latex]v\dfrac{d}{t}\text{or t=}\dfrac{D}{v}[/latex]
d = 500 m
t = find [latex]t =\dfrac{\text{500 m}}{\text{350 m/s}}[/latex] or 1.43 s ( ≈ 1.4 s)
Data for the jet traveling:
Mach 1.8 at 31°C = 1.8 x 350 m/s or 630 m/s
v = 630 m/s [latex]v=\dfrac{d}{t}[/latex] or d = v t
d = find
t = 1.43 s d = (630 m/s)(1.43 s)
d = 901 m (≈ 900 m)
QUESTIONS 14.4 The Doppler Effect and Shock Waves, continued...
9. If a jet is traveling at Mach 2.4, what is the Mach angle of the cone that is produced?
10. What is the Mach speed of a jet that is producing a Mach angle cone of of 32°?
11. What is the Mach angle of a space capsule or ship that enters the Earth’s atmosphere at Mach 23? Assume the speed of sound for this problem is Mach 1.2. (As the ship enters the atmosphere the speed of sound varies according to air pressure and temperature).
14.5.1 The initial test results in using sound to measure a vehicle speed
Four audio techs, Glen, Linda, Bob and Judy are working on an audio Doppler shift monitor that can be used to measure the speed of a moving object as long as the source frequency and the speed of sound remain constant. The data from their first test was a measure of 4100 Hz when the vehicle was moving towards them and 3900 Hz when moving away.
(i) Estimate the speed of the vehicle if the speed of sound on that day was 442 m/s.
(ii) What is the error in these measures if the speed of the vehicle is known to be 25 m/s?
(iii) How much is this error reduced if we are to take the average of these two speeds?
REFERENCES
1.Image Source: NOAA - Kelvin–Helmholtz instabilities taken over southern Missouri by pilot Shawn McCauley! These clouds look like breaking waves in the ocean because it is the same physical process.
2. Extra Help - Vibrations: https://www.physicsclassroom.com/class/waves/Lesson-0/Vibrational-Motion Extra Help - The Nature of a Wave: https://www.physicsclassroom.com/class/waves/Lesson-1/Waves-and-Wavelike-Motion
3. Article to Read - Massive Bolivian earthquake reveals mountains 660 kilometers below our feet: https://www.sciencedaily.com/releases/2019/02/190214153125.htm
4. Objects going through this Simple Harmonic Motion are known as Simple Harmonic Oscillators
5. Extra Help - What is a Wave?: https://www.physicsclassroom.com/class/waves/Lesson-1/What-is-a-Wave
6. Image Source: Valengilda/jStock/Getty Images
7. Extra Help - Categories of Waves: https://www.physicsclassroom.com/class/waves/Lesson-1/Categories-of-Waves
8. Extra Help - Energy Transport and the Amplitude of a Wave: https://www.physicsclassroom.com/class/waves/Lesson-2/Energy-Transport-and-the-Amplitude-of-a-Wave.
9. Extra Help - The Anatomy of a Wave: https://www.physicsclassroom.com/class/waves/Lesson-2/The-Anatomy-of-a-Wave
10. Article to Read - Space sound waves around Earth: Electrons whistle while they work?: https://www.sciencedaily.com/releases/2017/07/170717110434.htm
11. Video to Watch: What Does Sound Look Like: https://www.youtube.com/watch?time_continue=32&v=px3oVGXr4mo
12. Videos to Watch: Visualizing Ultrasound with Schlieren Optics: Part 1 - Traveling Waves and Reflections: https://www.youtube.com/watch?v=MBPh410Gnes Part 2 - Diffraction and Standing Waves: https://www.youtube.com/watch?v=VrgyKFBPQW4 Part 3 - Standing Waves in Colour: https://www.youtube.com/watch?v=doxDOlwEblg
13. In Research News - More Evidence of sound waves carrying mass: https://phys.org/news/2019-03-evidence-mass.html?fbclid=IwAR1VHDhDdXhuHHC7yBIoYagEwnyQCCkdFlAFtEooJdnCvgxG9AlYSMKyU6E
14. In Research News - Researchers find proteins that might restore damaged sound-detecting cells in the ear: https://medicalxpress.com/news/2019-08-proteins-sound-detecting-cells-ear.html?fbclid=IwAR1lp99I_cvXxe6JlwnUiQLvNlLIrfJDuHAKCxg_8FCpIfZbvQtImXbwmgY
15. Reference Article - Transverse and Longitudinal Waves: http://hyperphysics.phy-a
16. Extra Help - The Speed of a Wave: https://www.physicsclassroom.com/cl
17. Extra Help - Wave Speeds: http://hyperphysics.phy-astr.gsu.edu/hbase/Sound/souspe2.html
18. Extra Help - The Speed of Sound: https://www.physicsclassroom.com/class/sound/Lesson-2/The-Speed-of-Sound
19. Extra Help - Bulk Elastic Properties: http://hyperphysics.phy-astr.gsu.edu/hbase/permot3.html
20. Article to Read - The Sound So Loud That It Circled the Earth Four Times: http://nautil.us/issue/38/noise/the-sound-so-loud-that-it-circled-the-earth-four-times
21. This equation derived by Kenneth Mackenzie (1981) is fairly accurate. Link: https://asa.scitation.org/doi/10.1121/1.386919
22. Extra Help - Reflection, Refraction and Diffraction: https://www.physicsclassroom.com/class/waves/Lesson-3/Reflection,-Refraction,-and-Diffraction
23. The Normal is a line drawn at 90° from the reflecting surface.

