Chapter 3: Constant Acceleration and Accelerated Motion

Equations Introduced and Used for this Topic: (All equations can be written and solved as both scalar and vector)
| [latex]a =\Delta{v}[/latex] | [latex]\overrightarrow{a}=\Delta\dfrac{\overrightarrow{v}}{t}[/latex] |
| [latex]\Delta{v}=v_f-v_i[/latex] | [latex]v =\dfrac{(v_{i}+v_{f})}{2}[/latex] |
| [latex]v_{f} = v_{i} + at[/latex] | [latex]2ad = v_{f}^{2} - v_{i}^{2}[/latex] |
| [latex]d =v_{i}t =\dfrac{1}{2} at^{2}[/latex] | [latex]d=\dfrac{(v_i + v_f)}{2}[/latex] |
Where…
v is Average Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v}[/latex] is Average Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vi is Initial Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v_i}[/latex] is Initial Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
vf is Final Speed, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h)
[latex]\overrightarrow{v_f}[/latex] is Final Velocity, commonly measured in Metres/Second (m/s) or Kilometres/Hour (km/h) and includes a direction
∆d is Distance Travelled, commonly measured in Metres (m), Kilometres (km)
[latex]\overrightarrow\Delta{d}[/latex] is Change in Displacement, commonly measured in Metres (m), Kilometres (km)
a is Acceleration (deceleration is negative), measured in Metres per Second squared (m/s2)
[latex]\overrightarrow{a}[/latex] is Vector Acceleration, measured in Metres per Second squared (m/s2) and includes a direction
t is Time, commonly measured in Seconds (s) or Hours (h)

3.1 Average Acceleration
[latex]a =\dfrac{\Delta{t}}{t}[/latex] [latex]\overrightarrow{a}=\dfrac{\Delta{\overrightarrow{v}}}{t}[/latex]
[latex]\Delta{v} =v_f - v_i[/latex] [latex]\Delta{\overrightarrow{v}}=\overrightarrow{v_f} -\overrightarrow{v_i}[/latex]
which can be expanded to the form:
[latex]a=\dfrac{v_{f}-v_{i}}{t}[/latex] [latex]a=\dfrac{\overrightarrow{v}_{f}-\overrightarrow{v}_{i}}{t}[/latex]
Acceleration (and deceleration) are two commonly experienced phenomena by anyone who has ridden in a vehicle or an elevator or, more noticeably, on a ride at an amusement park. You notice acceleration as a change in either speed or velocity, as speeding up, slowing down or changing the direction you are traveling. All of these changes to your speed or velocity mean that you are experiencing some sort of acceleration 5.
Quantifying acceleration and deceleration specifically refers to the rate 6 of the increase or the decrease in an object’s speed (or velocity). This means that:
[latex]a =\dfrac{\Delta{v}}{t}[/latex] and since [latex]\Delta{v} =v_f = v_i[/latex] [latex]a =\dfrac{v_f - v_i}{t}[/latex]
The acceleration equation is written the same way for average vector acceleration, except that it has vector notion written over the vector variables.
There are a few distinctions in working with scalar and vector acceleration:
For Scalar Acceleration:
• Acceleration refers to the increase in an object’s speed.
• Deceleration refers to the decrease in an object’s speed (use a negative for this measure).
For Vector Acceleration:
• Acceleration refers to the change in velocity and can be a positive or a negative value.
The units for acceleration are generally given in base SI metric form of m/s2 or as ms-2.
You can run into the form of units used in the UK that is given as m/s.
The rationalization for using the UK units is the mental gymnastics of trying to understand time squared (s2).
The historical concept of acceleration is influenced by the experiments of various natural philosophers. The oldest surviving records of the study of motion is that of Aristotle (384-322 BC), who studied the motion of objects falling through water. Water, which is around 784 times the density of air, slows down the motion of any falling object so it can be more easily studied. Any object falling through water reaches a maximum speed (terminal velocity) in a short order of time, which means that it will then fall at a constant velocity downwards. More massive objects will take a longer time to reach terminal velocity when falling.
Aristotle interpreted these observations as follows:
• Heavy objects fall faster than lighter objects.
• The rate at which objects fall depends on the density of the medium they are falling through.
• Objects move according to the ratios of their composition of Earth, Water, Air and Fire. All natural motion therefore occurs to move all elements to their natural place in the universe.
While aware that objects could increase in speed, Aristotelian scholars thought that speed was related to the distance separating these four elements, and that as the distance decreased the speed increased. To Aristotelians, time had no importance in these changes of speed. Aristotle did distinguish between motion that he considered natural and motion caused by humans or other non-natural sources that he called violent (unnatural). This interpretation of agents acting on the motion of a body created the foundation of a concept called impetus 7 [is this meant to be a footnote?], where the motion of a body that was thrown would continue in that motion until the impetus initially imparted to it wore off or was exhausted. This concept was refined nearly a millennium later by John Philoponus (490-570) in his modification of the concept of violent motion.
The Middle Ages witnessed the first of the many challenges that eventually replaced Aristotelian theory. The Persian polymath Avinenna (930-1037) is credited for moving away from pure Aristotelian concepts. Avinenna claimed that the Philoponean theory of violent motion was motion that was dissipated by external agents, such as friction caused by moving through its medium, as the reason for the changes to violent motion of a body. In this, Avinenna predated Newton’s First Law of Motion. Persian scientists continued to develop concepts related to motion. Ibn al-Haytham (965-1039) linked the amount of acceleration to gravitational acceleration. Abū Rayḥān Muḥammad ibn Aḥmad Al-Bīrūnī (973-1048) and Abu’l-Barakāt al-Baghdādī (1080–1165) both constructed the foundations of what later became know as Newton’s Second Law of Motion, that related the external force acting on an object to the object’s acceleration. The great advances of Islamic science were lost in the total destruction of Baghdad and the House of Wisdom in 1258 during the Mongol invasion by Hulagu Khan. Because of this loss, scientific advancement in Persia slowly diminished and followed that of Egypt and Greece, rather than predating the explosion of European Science by hundreds of years.
European science began to develop in the late Middle Ages through the rediscovery of the works of Aristotle. The Black Death plague in 1348, which killed over one third of the population of Europe and reached higher numbers in urban centers where science was flourishing, prevented the Europeans from taking up the reins from the Persians. The Renaissance began in Italy with an infusion of Byzantine and Islamic scientists fleeing the destruction of the Byzantine Empire by the Ottoman Turks.
Galileo Galilei, perhaps one of the most famous of the Renaissance scientists, is falsely credited with some accomplishments, such as climbing the Leaning Tower of Pisa and dropping a heavy and a light metal ball together to prove that they fell at the same rate 8 [footnote?] (disproving Aristotle’s claim that they would fall at a different rate). Simon Stevin conducted the actual experiment in 1586, dropping two lead spheres (one ten times the weight of the other) from a church tower 10 metres above ground.
Galileo used an inclined ramp to slow down the acceleration of a falling object, demonstrating that the distance fallen by an object without any friction influencing the fall was proportional to the square of the time the object fell. Specifically:
d ∝ t2
The following examples all relate to the rate of change in an object’s speed or velocity and the acceleration acting on the object. We will be using the following equations for these examples.
[latex]a =\dfrac{\Delta{v}}{t}[/latex] [latex]\overrightarrow{a}=\dfrac{\Delta{\overrightarrow{v}}}{t}[/latex]
[latex]\Delta{v} =v_f - v_i[/latex] [latex]\Delta{\overrightarrow{v}}=\overrightarrow{v}_f-\overrightarrow{v}_i[/latex]
which can be expanded to the form:
[latex]a=\dfrac{v_f-v_i}{t}[/latex] [latex]a=\dfrac{\overrightarrow{v}_f-\overrightarrow{v}_i}{t}[/latex]
Example 3.1.1
If ICBC expects that a car can decelerate at 6.15 m/s2, what amount of time should be needed to brake to a stop if traveling at 90 km/h?
Data:
a = – 6.15 m/s2 Second … Find the change in speed:
∆v = 90 km/h to a full stop ∆v = vf – vi
(First … 90 km/h = 25 m/s)
t= find ∆v = 0 m/s – 25 m/s = – 25 m/s
Third … Find the time:
[latex]a =\dfrac{\Delta{v}}{t}[/latex] or [latex]t=\dfrac{\Delta{v}}{a}[/latex]
[latex]t=\dfrac{-25 m/s}{-6.15 m/s^2}[/latex] or 4.07 s (≈4.1 s)
Example 3.1.2
A common measure of acceleration (or deceleration) is to give values in terms of the average strength of the Earth’s gravity or gs. If one g is given the value of 9.8 m/s2, what amount of time is needed for a jet accelerating at 3.0 gs to reach a speed of 100 m/s from rest?
Data:
a = 3.0 g’s x 9.8 m/s2 /g or 29.4 m/s2 [latex]a =\dfrac{\Delta{v}}{t}[/latex] or [latex]t =\dfrac{\Delta{v}}{a}[/latex]
∆v = 100 m/s – 0 m/s or 100 m/s
t = Find [latex]t=\dfrac{100 m/s}{29.4 m/s^2}[/latex]
t = 3.4 s
Example 3.1.3
What is the average acceleration of an electron that changes its speed from rest to a speed of 3.00 x 106 m/s in 6.00 µs?
Data:
a = Find [latex]a =\dfrac{\Delta{v}}{t}[/latex]
∆v = 3.00 x 106 m/s
t = 6.0 µs or 6.00 x 10-6 s [latex]\dfrac{3.00\times10^6 m/s}{6.00\times10^{-6}s}[/latex]
a = 5.00 x 1011 m/s2
Example 3.1.4
If a startled driver has a response time of 1.80 s to step on the brakes of a car, what time is needed to stop in a school zone if traveling at 50 km/h and if the brakes decelerate the average car at 5.8 m/s2? 9
This solution has several parts … First the time to respond is 1.80 s or tresponse = 1.80 s
Second the time to brake …
First … 50 km/h ÷ 3.6 = 13.89 m/s
Second ∆v = vf – vi … ∆v = 0 m/s – 13.89 m/s = – 13.89 m/s
a = – 5.8 m/s2 [latex]a =\dfrac{\Delta{v}}{t}[/latex] or [latex]t =\dfrac{\Delta{v}}{a}[/latex]
∆v = – 13.89 m/s
t = Find [latex]t=\dfrac{-13.89 m/s}{- 5.8 m/s^2}[/latex]
t = 2.39 s (≈ 2.4 s)
Now … Total time is:
ttotal = tresponse + tbrake
ttotal = 1.8 s + 2.4 s or 4.2 s
3.1 Average Acceleration
- A downhill skier accelerates from rest to a speed of 15 m/s in a time of 3.0 s. What would be this skier’s average acceleration?
- A remote control car accelerates from 1.0 m/s to 6.8 m/s in 2.0 s. What was its average acceleration?
- Any object that is dropped from rest near the Earth’s surface will accelerate downwards at 9.8 m/s2 (9.8 m/s2 is known as 1 g or 1 gravity of acceleration). What should be the change in speed of an object that falls for 3.0 s? (Ignore air resistance).
- A high end sports car accelerates at 5.0 m/s2. What amount of time should it take to change its speed by 30 km/h?
- At high speeds, a particular automobile is capable of an acceleration of about 0.50 m/s2. At this rate how much times does it take to accelerate from 90 to 110 km/h?
- What amount of time is required to bring a car traveling at 110 km/h to a full stop, if the brakes decelerate the car at 6.0 m/s2?
- A quarter mile dragster can go from rest to 432 km/h in 6.0 s. What is the average acceleration of this car? Convert this acceleration to gs (gravities).
- An electron changes its speed from rest to 2.76 x 107 m/s in a time of 1.25 ns (nanosecond). What is the average acceleration acting on the electron?
- If an average undistracted driver has a response time of 0.50 s to step on the brakes of car, what time is needed to stop in a school zone when traveling at 30 km/h and if the brakes decelerate the average car at 6.0 m/s?
1 g is the measure of 1 earth gravity (9.8 m/s2), 2 g is 2 earth gravities (2 x 9.8 m/s2) etc.
1 ns (nanosecond) is 1 x 10-9 s. nano stands for 10-9
Research Report – WHO (2008) Speed Management Manual: https//apps.who.int/bitstream/handle/10665/43915/9782940395040_eng.pdf
3.2 Constant Accelerated Motion
| [latex]a =\dfrac{\Delta{v}}{t}[/latex] | [latex]\overrightarrow{a}=\dfrac{\Delta{\overrightarrow{v}}}{t}[/latex] |
|---|---|
| [latex]\Delta{v}=v_f - v_i[/latex] | [latex]v=\dfrac{(v_i + v_f)}{2}[/latex] |
| [latex]v_{f} = v_{i}+ at[/latex] | [latex]2ad = v_{f}^{2} - v_{i}^{2}[/latex] |
| [latex]d = v_{i}t +\dfrac{1}{2} at^{2}[/latex] | [latex]d =\dfrac{(v_i + v_f)t}{2}[/latex] |
The equations you choose to solve an accelerated problem can be found by using the chart shown below. How we choose which equation to use depends for the most part on which variable is not given or asked for. We can call these variables “not mentioned”.
The chart below indicates which of the four constant acceleration equations you can use for the variable that is not mentioned.
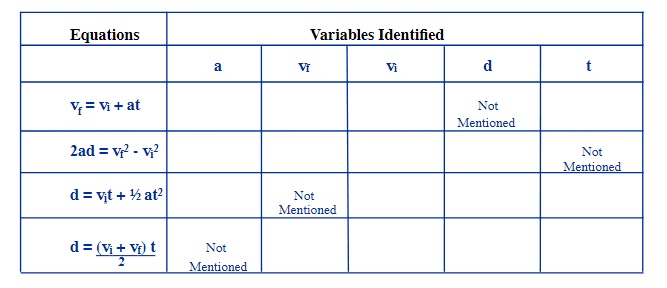
For example: You are given the following data in a problem:
a = some (constant) value
vi = some value The equation to use is …
vf = some value 2ad = vf2 – vi2
d = asked to find
t = not mentioned
If one encounters a setting where there is a constant average acceleration, it is possible to combine several equations together to create four accelerated motion equations. Specifically:
vf = vi + at 2ad = vf2 – vi2
d = vit + ½ at2 [latex]d =\dfrac{(v_i + v_f) t}{2}[/latex]
It is quite easy to show how two of these four equations are derived.
[latex]d =\dfrac{(v_i + v_f) t}{2}[/latex] is simply the expansion of d = v t (originally given as v = d/t) where the speed of the object has been replaced by taking the average of the initial and final speed (or velocity) [latex]v =\dfrac{(v_i + v_f)}{2}[/latex]
In this case you can see that:
For the equation d = v t when you replace [latex]v =\dfrac{(v_i + v_f)}{2}[/latex] you are left with [latex]d =\dfrac{(v_i + v_f) t}{2}[/latex]
vf = vi + at is simply the rearrangement of the basic acceleration equation a = ∆v/t
where ∆v is replaced with vf – vi and a = ∆v/t is rewritten as at = ∆v
When combined you are left with at = vf – vi more commonly written as vf = vi + at
The other two equations d = vit + ½ at2 and 2ad = vf2 – vi2 require a little more work to derive.
NOTE:
For these four equations to work correctly, the acceleration must be uniform or constant
Example 3.2.1
What is the average acceleration of a pickup truck that changes its speed from 60 km/h to 90 km/h in 6.0 s?
Data:
a = find Use vf = vi + at or [latex]=\dfrac{(v_f - v_i)}{t}[/latex]
vi = 60 km/h or 16.7 m/s
vf = 90 km/h or 25 m/s [latex]a=\dfrac{25 m/s - 16.7 m/s}{6.0 s}[/latex]
d = not mentioned a = 1.4 m/s2
t = 6.0 s
Example 3.2.2
If an object dropped from rest accelerates downwards at 9.8 m/s2 (one gravity or g), what distance should it have fallen after it fell for 4.0 s?
Data:
a = 9.8 m/s2 Use d = vit + ½ at2
vi = 0 m/s … dropped d = (0 m/s)(4.0 s) + 0.5(9.8 m/s2)(4.0s)2
vf = not mentioned d = 0 m + 78.4 m
d = find d = 78.4 m (≈ 78 m)
t = 4.0 s
Example 3.2.3
What distance does a vehicle travel when passing another vehicle if it constantly accelerates from 80 km/h to 115 km/h over 7.5 s?
Data:
a = not mentioned Use [latex]d =\dfrac{(v_i + v_f)t}{2}[/latex]
vi = 80 km/h or 22.2 m/s [latex]d =\dfrac{(22.2 m/s + 31.9 m/s)}{2}(7.5 s)[/latex] HELP
vf = 115 km/h or 31.9 m/s
d = find [latex]d =\dfrac{(54.1 m/s)}{2} (7.5 s)[/latex] HELP
t = 7.5 s
d = 203 m (≈ 200 m)
Example 3.2.4
A texting driver takes 6.0 s to notice he or she needs to brake to a stop when traveling at 120 km/h. If we use ICBC’s estimation that the average vehicle can decelerate at 6.15 m/s2, what distance would this vehicle travel before coming to a complete stop?
Data for distracted driving:
v = 120 km/h or 33.3 m/s Use [latex]v =\dfrac{d}{t}[/latex] or d = v t
d = find d = (33.3 m/s)(6.0s)
t = 6.0 s d = 200 m
Data for braking:
a = – 6.15 m/s2 Use 2ad = vf2 – vi2
vi = 120 km/h or 33.3 m/s 2 (- 6.15 m/s2) d = (0 m/s)2 – (33.3 m/s)2
vf = 0 m/s … stopped (-12.3 m/s2) d = – 1111 m2/s2
d = find [latex]d =\dfrac{- 1111 m^2/s^2}{-12.3 m/s^2}[/latex]
t = not mentioned
d = 90.3 m (≈ 90 m)
Total distance driven: dtotal = ddistracted + dbraking
dtotal = 200 m + 90.3 m
dtotal = 290 m
The above examples all relate to the constant acceleration of a body in a straight line. In all cases the speed of the object will be changing. It is also possible to have an object experience constant acceleration but not have any change in speed. This occurs for an object traveling in a circular path, such as a planet orbiting the sun or a satellite orbiting a planet.
All motion depends on the direction of the accelerating that is acting on the body. If it acts in the same direction (or opposite to the direction) that the body moves, the speed will change. If this acceleration is acting at 90° to the direction of motion, then the object will move in a circular path, remaining at the exact same speed but constantly changing its velocity. Motion in a circular path will be studied much later in this text.
Attack of the Killer Tomatoes by ToHo Scope under the public domain.
3.2 Constant Accelerated Motion
- A baseball pitcher requires 0.1 s to accelerate a ball from rest to a speed of 30 m/s. Calculate the average acceleration acting on this ball.
- An object starting from rest accelerates at 10 m/s2. (i) What distance would it travel in 0.50 s? (ii) What speed does it reach in 0.50 s?
- A bicyclist has a speed of 6.0 m/s at the top of a hill, when he/she begins to accelerate at 2.0 m/s2. (i) What amount of time is needed for this person to reach a speed of 15 m/s? (ii) What distance does this person ride downhill during this time?
- What distance does a sports car accelerating at 3.0 m/s2 need to go from: (i) 0 m/s to 15 m/s? (ii) 15 m/s to 30 m/s?
- A small plane touches down at 30 m/s and decelerates to a full stop 6.0 s later. How far did it travel in this time?
- A small car accelerates from rest at a rate of 5.2 m/s2 over a distance of 80 m before running into the rear of a pickup. At what speed was the small car traveling when the collision occurred?
- A small pickup required 6.0 s to come to a full stop from an initial speed of 108 km/h. (i) What was the average deceleration acting on this pickup while braking? (ii) What amount of time should be needed to stop this pickup when traveling at 144 km/h? (Use the acceleration found in par (i)).
- If it takes just 2.0 s to brake a car from 30 m/s to 20 m/s, what amount of time should be needed to brake the same car from 15 m/s to a full stop?
- A car starting at 36 km/h accelerates at 2.0 m/s2 for 1/2 a kilometre. What is the final speed reached by this car?
- What deceleration acts on a skier that stops in 40 m if initially traveling at 72 km/h?
- A truck accelerates from 40 km/h to 80 km/h in 5.0 s. What is its acceleration in m/s2 and what distance did it travel in this time?
- What is the expected distance a car will stop if traveling at 108 km/h and can brake with an average deceleration of 6.15 m/s2?
- A tourist is traveling at 110 km/h when she beings to read a sign on the side of the road. For what amount of distance was she unaware of what was on the road, if it took her 5 s to read this sign?
- You are driving 100 km/h and see a bunny run out in front of you. It takes you 0.75 s to apply your brakes. What distance do you travel in this time?
3.3 Accelerate Motion. These take more time to solve
- The average well-maintained car should be able to decelerate at 0.6 g’s. What distance is required to bring this car to a full stop upon braking, when originally travelling at 120 km/h?
- A person who is properly constrained by a shoulder harness has a good chance of surviving a car collection if the deceleration does not exceed 30 g’s. Assuming uniform deceleration at this rate, calculate the distance over which the front end of the car must be designed to collapse if a crash occurs at 100 km/h.
- Granny is 5.0 m away from safety. A killer tomato is 3.0 m behind Granny. Hearing a noise Granny turns and sees the killer tomato and begins to accelerate her wheelchair at 0.75 m/s2 towards safety. The killer tomato chases after her accelerating at 1.0 m/s2. Does Granny make it?
- A 100 m long train accelerates uniformly from rest. If the front of the train passes a railway worker 150 m down the track at a speed of 25 m/s, what will be the speed of the last car as it passes the worker?

Road Safety from the ICBC website. We need to contact them to use this image at email trademark@icbc.com
3.4.1 ICBC Road Sense Campaign
Question: Calculate the deceleration in gs for the car crash used in this ICBC promotion.
3.4.2 Star Trek Discovery Episode “The Vulcan Hello”
“Investigation a damaged satellite near a binary star system on the edge of Federation space, the crew members of the USS Shenzhou discover an object obscured from their sensors. After First Officer Michael Burnham volunteers to investigate the object, she finds an ancient, carved vessel. She is attacked by a Klingon, and when trying to escape, she accidentally kills him. A group of Klingons mourn the death of their soldier, dubbed the “Torchbearer”, before the outcast Voq volunteers to take his place. The Klingons, led by T’Kuvma, reveal themselves in a cloakable ship. T’Kuvma preaches to his followers of the Federation’s attempts to usurp the individuality of the Klingons and their culture, and plans to fulfill an ancient prophecy by uniting the 24 great Klingon houses as was once done by Kahless. Voq activates a beacon that summons the Klingon leaders. Burnham, desperate to prevent a war, attempts to fire on the Klingons first, against the wishes of Captain Philippa Georgiou. Burnham is arrested for mutiny.”
At the start of this episode Michael Burnham dons a space suit with a transport pack that takes her 2000 km in 6 minutes. The fastest way to travel this distance is to accelerate towards the spaceship for 3 minutes (the first 1000 km) and then decelerate for the remaining 3 minutes to travel the remaining 1000 km to stop at the ship.
Question: Estimate the number of gs’ acceleration Burnham experiences.

REFERENCES
1. Image is of the “Blazing Angel Jet Dragster” 582 kg with a Pratt & Whitney Jet Engine delivering 8000+ hp.
Source: https://commons.wikimedia.org/wiki/File:Blazing_Angel_Jet_Dragster.jpg
2. A-Level Physics Tutor: http://www.a-levelphysicstutor.com/index-mech.php
3. Extra Help – The Kinematic Equations: LINK NOT FOUND https://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic Equations
4. Extra Help – Acceleration: https://www.physicsclassroom.com/class/1DKin/Lesson-1/Acceleration
5. It is possible to experience acceleration without being able to detect it.
6. Rate is a measure of the change of something over the time it takes
7. Impetus and the study of impulse & momentum are covered later in this text
8. While claiming that Galileo did do the drop of the the two spheres, NASA astronaut David Scott in the Apollo 15 lunar mission dropped hammer and a feather on the Moon, crediting Galileo Galilei: https://moon.nasa.gov/resources/331/the-apollo-15-hammer-feather-drop
9. Article to Read – Cambridge study finds driverless cars working together can speed u traffic by 35%: https://www.greencarcongress.com/2019/05/20190520-cambridge.html

