26 4.3 Linear Absolute Value Inequalities
Absolute values are positive magnitudes, which means that they represent the positive value of any number.
For instance, | −5 | and | +5 | are the same, with both having the same value of 5, and | −99 | and | +99 | both share the same value of 99.
When used in inequalities, absolute values become a boundary limit to a number.
Example 4.3.1
Consider \(| x | < 4.\)
This means that the unknown \(x\) value is less than 4, so \(| x | < 4\) becomes \(x < 4.\) However, there is more to this with regards to negative values for \(x.\)
| −1 | is a value that is a solution, since 1 < 4.
However, | −5 | < 4 is not a solution, since 5 > 4.
The boundary of \(| x | < 4\) works out to be between −4 and +4.
This means that \(| x | < 4\) ends up being bounded as \(-4 < x < 4.\)
If the inequality is written as \(| x | \le 4\), then little changes, except that \(x\) can then equal −4 and +4, rather than having to be larger or smaller.
This means that \(| x | \le 4\) ends up being bounded as \(-4 \le x \le 4.\)
Example 4.3.2
Consider \(|x| > 4.\)
This means that the unknown \(x\) value is greater than 4, so \(|x| > 4\) becomes \(x > 4.\) However, the negative values for \(x\) must still be considered.
The boundary of \(|x| > 4\) works out to be smaller than −4 and larger than +4.
This means that \(|x| > 4\) ends up being bounded as \(x < -4 \text{ or } 4 < x.\)
If the inequality is written as \(| x | \ge 4,\) then little changes, except that \(x\) can then equal −4 and +4, rather than having to be larger or smaller.
This means that \(|x| \ge 4\) ends up being bounded as \(x \le -4 \text{ or } 4 \le x.\)
When drawing the boundaries for inequalities on a number line graph, use the following conventions:
For ≤ or ≥, use [brackets] as boundary limits.![]()
For < or >, use (parentheses) as boundary limits. ![]()
| Equation | Number Line |
|---|---|
| \(| x | <4 \) |  |
| \(| x | \le 4\) |  |
| \(| x | > 4\) |  |
| \(| x | \ge 4\) |  |
When an inequality has an absolute value, isolate the absolute value first in order to graph a solution and/or write it in interval notation. The following examples will illustrate isolating and solving an inequality with an absolute value.
Example 4.3.3
Solve, graph, and give interval notation for the inequality \(-4 - 3 | x | \ge -16.\)
First, isolate the inequality:
\[\begin{array}{rrrrrl}
-4&-&3|x|& \ge & -16 &\\
+4&&&&+4& \text{add 4 to both sides}\\
\hline
&&\dfrac{-3|x|}{-3}& \ge & \dfrac{-12}{-3}&\text{divide by }-3 \text{ and flip the sense} \\ \\
&&|x|&\le & 4 &&
\end{array}\]
At this point, it is known that the inequality is bounded by 4. Specifically, it is between −4 and 4.
This means that \(-4 \le | x | \le 4.\)
This solution on a number line looks like:

To write the solution in interval notation, use the symbols and numbers on the number line: \([-4, 4].\)
Other examples of absolute value inequalities result in an algebraic expression that is bounded by an inequality.
Example 4.3.4
Solve, graph, and give interval notation for the inequality \(| 2x - 4 | \le 6.\)
This means that the inequality to solve is \(-6\le 2x - 4\le 6\):
\(\begin{array}{rrrcrrr}
-6&\le & 2x&-&4&\le & 6 \\
+4&&&+&4&&+4 \\
\hline
\dfrac{-2}{2}&\le &&\dfrac{2x}{2}&&\le & \dfrac{10}{2} \\ \\
-1 &\le &&x&&\le & 5
\end{array}\)

To write the solution in interval notation, use the symbols and numbers on the number line: \([-1,5].\)
Example 4.3.5
Solve, graph, and give interval notation for the inequality \(9 - 2 | 4x + 1 | > 3.\)
First, isolate the inequality by subtracting 9 from both sides:
\[\begin{array}{rrrrrrr}
9&-&2|4x&+&1|&>&3 \\
-9&&&&&&-9 \\
\hline
&&-2|4x&+&1|&>&-6 \\
\end{array}\]
Divide both sides by −2 and flip the sense:
\[\begin{array}{rrr}
\dfrac{-2|4x+1|}{-2}&>&\dfrac{-6}{-2} \\ \\
|4x+1|&<& 3
\end{array}\]
At this point, it is known that the inequality expression is between −3 and 3, so \(-3 < 4x + 1 < 3.\)
All that is left is to isolate \(x\). First, subtract 1 from all three parts:
\[\begin{array}{rrrrrrr}
-3&<&4x&+&1&<&3 \\
-1&&&-&1&&-1 \\
\hline
-4&<&&4x&&<&2 \\
\end{array}\]
Then, divide all three parts by 4:
\[\begin{array}{rrrrr}
\dfrac{-4}{4}&<&\dfrac{4x}{4}&<&\dfrac{2}{4} \\ \\
-1&<&x&<&\dfrac{1}{2} \\
\end{array}\]
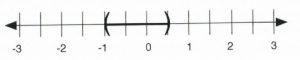
In interval notation, this is written as \(\left(-1,\dfrac{1}{2}\right).\)
It is important to remember when solving these equations that the absolute value is always positive. If given an absolute value that is less than a negative number, there will be no solution because absolute value will always be positive, i.e., greater than a negative. Similarly, if absolute value is greater than a negative, the answer will be all real numbers.
This means that:
\(\begin{array}{c}
| 2x - 4 | < -6 \text{ has no possible solution } (x \ne \mathbb{R}) \\ \\
\text{and} \\ \\
| 2x - 4 | > -6 \text{ has every number as a solution and is written as } (-\infty, \infty)
\end{array}\)
Note: since infinity can never be reached, use parentheses instead of brackets when writing infinity (positive or negative) in interval notation.
Questions
For questions 1 to 33, solve each inequality, graph its solution, and give interval notation.
- \(| x | < 3\)
- \(| x | \le 8\)
- \(| 2x | < 6\)
- \(| x + 3 | < 4\)
- \(| x - 2 | < 6\)
- \(| x - 8 | < 12\)
- \(| x - 7 | < 3\)
- \(| x + 3 | \le 4\)
- \(| 3x - 2 | < 9\)
- \(| 2x + 5 | < 9\)
- \(1 + 2 | x - 1 | \le 9\)
- \(10 - 3 | x - 2 | \ge 4\)
- \(6 - | 2x - 5 | > 3\)
- \(| x | > 5\)
- \(| 3x | > 5\)
- \(| x - 4 | > 5\)
- \(| x + 3 | > 3\)
- \(| 2x - 4 | > 6\)
- \(| x - 5 | > 3\)
- \(3 - | 2 - x | < 1\)
- \(4 + 3 | x - 1 | < 10\)
- \(3 - 2 | 3x - 1 | \ge -7\)
- \(3 - 2 | x - 5 | \le -15\)
- \(4 - 6 | -6 - 3x | \le -5\)
- \(-2 - 3 | 4 - 2x | \ge -8\)
- \(-3 - 2 | 4x - 5 | \ge 1\)
- \(4 - 5 | -2x - 7 | < -1\)
- \(-2 + 3 | 5 - x | \le 4\)
- \(3 - 2 | 4x - 5 | \ge 1\)
- \(-2 - 3 | - 3x - 5| \ge -5\)
- \(-5 - 2 | 3x - 6 | < -8\)
- \(6 - 3 | 1 - 4x | < -3\)
- \(4 - 4 | -2x + 6 | > -4\)

