99 11.1 Function Notation
There is a special classification of mathematical relationships known as functions. So far, you will have unknowingly worked with many functions, where the defining characteristic is that functions have at most one output for any input. Properties of addition, subtraction, multiplication or division all bear the needed traits of being functions. For instance, 2 × 3 will always be 6. Formally, functions are defined in equations in terms of \(x\) and \(y\), where there will only be one \(y\) output for any single \(x\) input. An equation is not considered a function if more than one \(y\) variable can be found for any \(x\) variable.
This means that the definition of a function, in terms of equations in \(x\) and \(y\), is that, for any \(x\)-value, there is at most one \(y\)-value that corresponds with it.
One way to use this definition to see if an equation represents a function is to look at its graph. This is done by looking at any \(x\)-value to see if there exists more than one corresponding \(y\)-value. The name for this check is the vertical line test. The vertical line test is defined by trying to find if any vertical drawn line will intersect more than one \(y\)-value. If you can find any instance of this on the graph, then the equation drawn is not a function. For instance:
Example 11.1.1
Are all the mathematical relationships shown below functions?
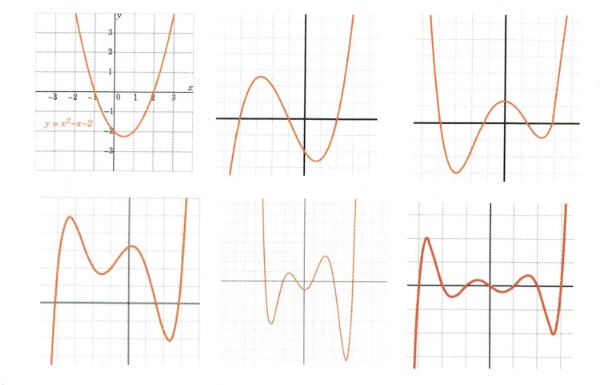
Solution: All of these are functions, since it is impossible to find any vertical line to cross more than one \(y\)-value.
Example 11.1.2
Are any of the mathematical relationships shown below functions?
Solution: None of these are functions, since vertical lines can easily be drawn that will have 2 or more \(y\)-values for a single \(x\)-value.
Deciding if equations are functions requires more effort than using the vertical line test. The easiest method is to isolate the \(y\)-variable and see if it results in two potential \(x\)-values.
Example 11.1.3
Is the equation \(0 = 2x^2 - y - 7\) a function?
First, you need to isolate the \(y\)-variable:
\[\begin{array}{rrrrrrr}
0&=&2x^2&-&y&-&7 \\
+y&&&+&y&& \\
\hline
y&=&2x^2&-&7&&
\end{array}\]
There is only one solution for \(y\) for any given value of \(x\). Therefore, this equation is a function.
The next example shows an equation that is not a function, since there are two \(y\)-values for every given \(x\)-value.
Example 11.1.4
Is the equation \(0 = y^2 - 5x - 7\) a function?
First, you need to isolate the \(y\)-variable:
\[\begin{array}{rrrrrrr}
0&=&y^2&-&5x^2&-&7 \\
-y^2&&-y^2&&&& \\
\hline
-y^2&=&-5x^2&-&7&&
\end{array}\]
Next, we remove the negatives by multiplying the entire equation by −1:
\[y^2=5x^2+7\]
To reduce the square, take the square root of both sides:
\[y=\pm (5x^2+7)^{\frac{1}{2}}\]
We are left with two solutions for any single \(x\)-variable. Therefore, this equation is not a function.
Example 11.1.5
Is the equation \(x = | y - 5 |\) a function?
Solving for \(y\) yields \(y - 5 = x\) and \(y - 5 = -x\).
Isolating for \(y\) yields \(y = x + 5\) and \(y = -x + 5\).
You are left with the same type of solution as you did when taking the square root, except in this case, \(y = \pm x + 5\).
We are left with two solutions for any single \(x\) variable. Therefore, this equation is not a function
Excluded Values and Domains of a Function
When working with functions, one needs to identify what values of \(x\) cannot be used. These \(x\)-values are termed the excluded values and are useful in defining the domain of a function. The logic of excluded values is the extension of a property from arithmetic:
\[\text{You cannot divide by zero, or Never divide by zero}\]
Example 11.1.6
Find the excluded values of the following function:
\[y=\dfrac{2x^2-3}{(x-2)(x+3)(x-1)}\]
In this example, there will be 3 excluded values:
\[(x - 2) \neq 0\hspace{0.25in} (x + 3) \neq 0\hspace{0.25in} (x - 1) \neq 0\]
Since these terms are all in the denominator of this function, any value that can make one of them equal zero must be excluded.
For these terms, those excluded values are \(x \neq 2, x \neq -3\) and \(x \neq 1\).
Interpreting this means that the domain of \(x\) is any real number except for the excluded values.
You write this as:
domain of \(x\) = all real numbers except 2, −3, 1
More formally:
\[\text{domain} = \{x | x \in \mathbb{R} , x \neq 2, -3, 1\}\]
Finding the domains of radicals can lead to an inequality as a solution, since any real solution of an even-valued radical is restricted in that the value inside the radical cannot be negative.
Example 11.1.7
Find the excluded values of the following function: \(y = \sqrt{2x - 3}\).
Since its impossible to take any real root of a negative inside a radical, the value inside the radical must always be zero or larger. This means:
\[\begin{array}{rrrrr}
2x&-&3&\ge &0 \\
&+&3& &+3 \\
\hline
&&\dfrac{2x}{2}&\ge &\dfrac{3}{2} \\ \\
&&x&\ge &\dfrac{3}{2}
\end{array}\]
The domain for \(x\) is such that \(x\) must always be greater than or equal to \(\dfrac{3}{2}\).
Function Notation
The earliest written usage of function notation \(f(x)\) appears in the works of Leonhard Euler in the early 1700s. If you have an equation that is found to be a function, such as \(y = 2x^2 - 3x + 2\), it can also be written as \(f(x) = 2x^2 - 3x + 2\). It can be useful to write a function equation in this form.
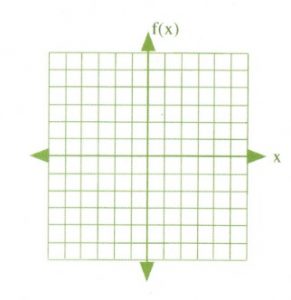 You should quickly notice that, in graphing these functions, the \(y\)-variable is replaced by the function notation \(f(x)\) for the \(y\)-axis. That \(f(x)\) replaces \(y\) is the main change.
You should quickly notice that, in graphing these functions, the \(y\)-variable is replaced by the function notation \(f(x)\) for the \(y\)-axis. That \(f(x)\) replaces \(y\) is the main change.
When drawing a graph of the function, \(f(x)\) is treated as if it is the \(y\)-variable.
Evaluating Functions
One of the features of function notation is the way it identifies values of the function for given \(x\) inputs. For instance, suppose you are given the function \(f(x) = 3x^2 - 5\) and you are asked to find the value of the \(f(x)\) when \(x = 7\). This would be written as \(f(7)\) and you would be asked to evaluate \(f(7) = 3x^2 - 5\). The following examples illustrate this process.
Example 11.1.8
Evaluate the function \(f(x) = 3x^2 - 2x + 5\) for \(f(4)\).
First, you need to replace all values of \(x\) with the value 4. This looks like:
\[\begin{array}{rrl}
f(4)&=&3(4)^2-2(4)+5 \\
f(4)&=&3(16)-8+5 \\
f(4)&=&48-8+5 \\
f(4)&=&45
\end{array}\]
Functions can be written using other letters outside of the standard \(f\). In fact, just about any letter will suffice. For instance, for the equation \(y = 3x^4 - 8\), this can be written in function notation as \(f(x) = 3x^4 - 8\), \(g(x) = 3x^4 - 8\), \(h(x) = 3x^4 - 8\), \(k(x) = 3x^4 - 8\), \(p(x) = 3x^4 - 8\), and so on.
Example 11.1.9
Evaluate the function \(h(t) = 3t^2 + 7t + 2\) for \(h(-1)\).
First, you need to replace all values of \(t\) with the value −1. This looks like:
\(h(-1) = 3(-1)^2 + 7(-1) + 2\), which simplifies to \(h(-1) = -2\)
Questions
- Which of the following are functions?
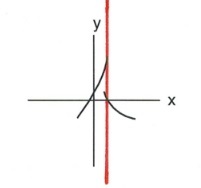
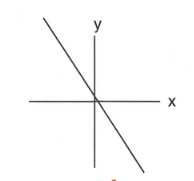
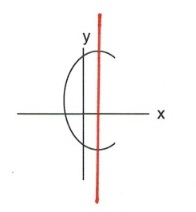
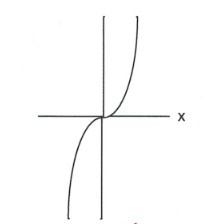
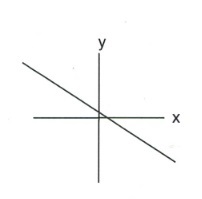
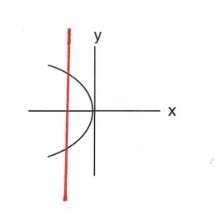
- \(y = 3x - 7\)
- \(y^2 - x^2 = 1\)
- \(\sqrt{y} + x = 2\)
- \(x^2 + y^2 = 1\)
Specify the domain of each of the following functions.
- \(f(x) = -5x + 1\)
- \(f(x) = \sqrt{5 - 4x}\)
- \(s(t) = \dfrac{1}{t^2}\)
- \(f(x) = x^2 - 3x - 4\)
- \(s(t) = \dfrac{1}{t^2+1}\)
- \(f(x) = \sqrt{x - 16}\)
- \(f(x) = \dfrac{-2}{x^2 - 3x - 4}\)
- \(h(x) = \dfrac{\sqrt{3x - 12}}{x^2 - 25}\)
Evaluate each of the following functions.
- \(g(x) = 4x - 4\text{ for } g(0)\)
- \(g(n) = -3 \cdot 5^{-n}\text{ for }g(2)\)
- \(f(x) = x^2 + 4\text{ for }f(-9)\)
- \(f(n) = n - 3\text{ for }f(10)\)
- \(f(t) = 3^t - 2\text{ for } f(-2)\)
- \(f(a) -3^{a - 1} - 3\text{ for }f(2)\)
- \(k(x)=-2\cdot 4^{2x-2}\text{ for }k(2)\)
- \(p(t)=-2\cdot 4^{2t+1}+1\text{ for }p(-2)\)
- \(h(x)=x^3+2\text{ for }h(-4x)\)
- \(h(n)=4n+2\text{ for }h(n+2)\)
- \(h(x)=3x+2\text{ for }h(-1+x)\)
- \(h(a)=-3\cdot 2^{a+3}\text{ for }h\left(\dfrac{1}{3}\right)\)
- \(h(x)=x^2+1\text{ for }h(x^4)\)
- \(h(t)=t^2+t\text{ for }h(t^2)\)
- \(f(x)=|3x+1|+1\text{ for }f(0)\)
- \(f(n)=-2|-n-2|+1\text{ for }f(-6)\)
- \(f(t)=|t+3|\text{ for }f(10)\)
- \(p(x)=-|x|+1\text{ for }p(5)\)

