Midterm 2: Version E Answer Key

[latexpage]

1. \(x-y=-3\)

   \(x\)	\(y\)
   0	3
   −3	0

   \(x+2y=3\)

   \(x\)	\(y\)
   3	0
   0	\(\dfrac{3}{2}\)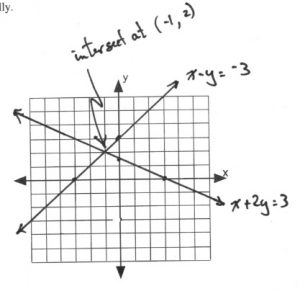

   

2. \(\begin{array}{rrrrrl}
   \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
   &(2x&-&5y&=&-2)(-3) \\
   &(3x&-&4y&=&\phantom{-}4)(2) \\ \\
   &-6x&+&15y&=&6 \\
   +&6x&-&8y&=&8 \\
   \midrule
   &&&7y&=&14 \\
   &&&y&=&2 \\ \\
   &2x&-&5(2)&=&-2 \\
   &2x&-&10&=&-2 \\
   &&+&10&&+10 \\
   \midrule
   &&&2x&=&8 \\
   &&&x&=&4
   \end{array}\)
   \((4,2)\)
3. \(\begin{array}{rrrrrl}
   \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
   &(4x&+&3y&=&-29)(-2) \\
   &(3x&+&2y&=&-21)(3) \\ \\
   &-8x&-&6y&=&\phantom{-}58 \\
   +&9x&+&6y&=&-63 \\
   \midrule
   &&&x&=&-5 \\ \\
   &3(-5)&+&2y&=&-21 \\
   &-15&+&2y&=&-21 \\
   +&15&&&&+15 \\
   \midrule
   &&&2y&=&-6 \\
   &&&y&=&-3
   \end{array}\)
   \((-5,-3)\)
4. \(\begin{array}{ll}
   \begin{array}{rrrrrrrl}
   \\ \\ \\ \\ \\ \\ \\ \\
   &(x&+&y&-&3z&=&0)(-2) \\ \\
   &-2x&-&2y&+&6z&=&0 \\
   +&2x&-&3y&&&=&16 \\
   \midrule
   &&&-5y&+&6z&=&16 \\ \\
   &&&(2y&-&2z&=&-12)(3) \\ \\
   &&&6y&-&6z&=&-36 \\
   +&&&-5y&+&6z&=&\phantom{-}16 \\
   \midrule
   &&&&&y&=&-20
   \end{array}
   & \hspace{0.25in}
   \begin{array}{rrrrr}
   \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
   2x&-&3y&=&16 \\
   2x&-&3(-20)&=&16 \\
   2x&+&60&=&16 \\
   &&-60&&-60 \\
   \midrule
   &&2x&=&-44 \\
   &&x&=&-22 \\ \\
   2y&-&2z&=&-12 \\
   2(-20)&-&2z&=&-12 \\
   -40&-&2z&=&-12 \\
   +40&&&&+40 \\
   \midrule
   &&-2z&=&28 \\
   &&z&=&-14
   \end{array}
   \end{array}\)
   \((-22,-20,-14)\)
5. \(5-4\left[2x-2\cancel{(6x-5)^0}1-(7-2x)\right]\)
   \(5-4\left[2x-2(1)-7+2x\right]\)
   \(5-4\left[4x-9\right]\)
   \(5-16x+36\)
   \(-16x+41\)
6. \(3ab^4(a^2-25)\)
   \(3a^3b^4-75ab^4\)
7. \(\begin{array}{rrrrrlrrrr}
   \\ \\ \\ \\ \\ \\
   &x^2&+&3x&-&6&&&& \\
   \times &x^2&+&3x&-&6&&&& \\
   \midrule
   &x^4&+&3x^3&-&6x^2&&&& \\
   &&&3x^3&+&9x^2&-&18x&& \\
   +&&&&-&6x^2&-&18x&+&36 \\
   \midrule
   &x^4&+&6x^3&-&3x^2&-&36x&+&36
   \end{array}\)
8. \(\polylongdiv{3x^3+18+7x^2}{x+3}\)
9. \(x^2-3z+7x-21\)
   \(x(x-3)+7(x-3)\)
   \((x-3)(x+7)\)
10. \(4x^2(x+1)-9(x+1)\)
    \((x+1)(4x^2-9)\)
    \((x+1)(2x-3)(2x+3)\)
11. \((2x)^3-(3y)^3\)
    \((2x-3y)(4x^2+6xy+9y^2)\)
12. \(x^4-625x^2+x^2-625\)
    \(x^2(x^2-625)+1(x^2-625)\)
    \((x^2+1)(x^2-625)\)
    \((x^2+1)(x-25)(x+25)\)
13. \(\phantom{1}\)
    \(B+G=20\Rightarrow B=20-G \\ \)
    \(\begin{array}{rrrrrrrrrl}
    &G&-&4&=&2(B&-&4)&& \\
    &G&-&4&=&2B&-&8&& \\ \\
    &G&-&4&=&2(20&-&G)&-&8 \\
    &G&-&4&=&40&-&2G&-&8 \\
    &G&-&4&=&32&-&2G&& \\
    +&2G&+&4&&4&+&2G&& \\
    \midrule
    &&&3G&=&36&&&& \\
    &&&G&=&12&&&& \\ \\
    &&&B&=&20&-&G&& \\
    &&&B&=&20&-&12&=&8 \\
    \end{array}\)
14. \(\phantom{1}\)
    \(x=16\%\text{ solution} \\ \)
    \(\begin{array}{rrrrrrrr}
    &16x&+&6(20)&=&12(x&+&20) \\
    &16x&+&120&=&12x&+&240 \\
    -&12x&-&120&&-12x&-&120 \\
    \midrule
    &&&4x&=&120&& \\ \\
    &&&x&=&\dfrac{120}{4}&=&30\text{ ml} \\
    \end{array}\)
15. \(\begin{array}{rrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    &(C&+&R&=&60)(-3.40) \\ \\
    &-3.40C&-&3.40R&=&-204 \\
    +&3.40C&+&3.90R&=&\phantom{-}213\\
    \midrule
    &&&0.50R&=&\phantom{-}9 \\ \\
    &&&R&=&\dfrac{9}{0.50}\text{ or 18 kg} \\ \\
    &C&+&R&=&\phantom{-}60 \\
    &C&+&18&=&\phantom{-}60 \\
    &&-&18&&-18 \\
    \midrule
    &&&C&=&\phantom{-}42\text{ kg}
    \end{array}\)