Midterm 1: Version A Answer Key
- \(\begin{array}{l}
\\ \\ \\ \\ \\ \\ \\ \\
-(-3)-\sqrt{(-3)^2-4(4)(-1)} \\ \\
3-\sqrt{9+16} \\ \\
3-\sqrt{25} \\ \\
3-5 \\ \\
-2
\end{array}\) - \(\begin{array}{rrrrrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\
&2x&-&10&-&85&=&3&-&9x&-&54 \\
+&9x&+&10&+&85&&&+&9x&+&3 \\
&&&&&&&&&&+&85 \\
&&&&&&&&&&+&10 \\
\hline
&&&&&\dfrac{11x}{11}&=&\dfrac{44}{11}&&&& \\ \\
&&&&&x&=&4&&&&
\end{array}\) - \(\begin{array}{rrl}
\\ \\ \\ \\ \\
A(B-b)&=&h \\ \\
B-b&=&\dfrac{h}{A} \\ \\
-b&=&\dfrac{h}{A}-B
\end{array}\) - \(\phantom{1}\)
\(\left(\dfrac{x+1}{4}-\dfrac{5}{8}=\dfrac{x-1}{8}\right)(8) \\ \)
\(\begin{array}{rrrrrrrrr}
2(x&+&1)&-&5&=&x&-&1 \\
2x&+&2&-&5&=&x&-&1 \\
-x&-&2&+&5&&-x&+&5 \\
&&&&&&&-&2 \\
\hline
&&&&x&=&2&&
\end{array}\) 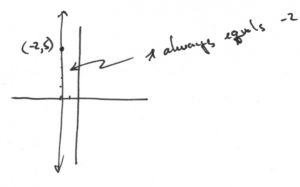
\(x=-2\)- \(\begin{array}{ll}
\\ \\ \\
\begin{array}{rrl}
m&=&\dfrac{\Delta y}{\Delta x} \\ \\
\dfrac{2}{5}&=&\dfrac{y--2}{x--1}
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrrrrrl}
\\ \\ \\
&&2(x&+&1)&=&5(y&+&2) \\
&&2x&+&2&=&5y&+&10 \\
&&-5y&-&10&&-5y&-&10 \\
\hline
2x&-&5y&-&8&=&0&& \\
&&&&0&=&2x&-&5y-8 \\ \\
&&&&y&=&\dfrac{2}{5}x&-&\dfrac{8}{5}
\end{array}
\end{array}\) - \(\begin{array}{ll}
\\ \\ \\ \\ \\ \\ \\
\begin{array}{rrl}
\text{1st slope} && \\
m&=&\dfrac{\Delta y}{\Delta x} \\ \\
m&=&\dfrac{4-0}{6--2} \\ \\
m&=&\dfrac{4}{8}\text{ or }\dfrac{1}{2}
\end{array}
& \hspace{0.25in}
\begin{array}{rrl}
\\ \\ \\ \\
\text{Now:} && \\
m&=&\dfrac{\Delta y}{\Delta x} \\ \\
\dfrac{1}{2}&=&\dfrac{y-0}{x--2} \\ \\
1(x+2) &=&2(y-0) \\
x+2&=&2y \\ \\
\therefore y&=&\dfrac{1}{2}+1 \\ \\
\text{or }x-2y+2&=&0
\end{array}
\end{array}\) 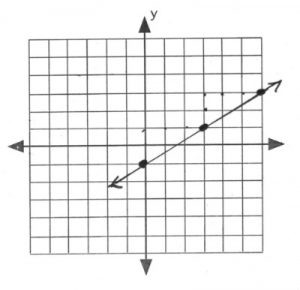
- \(\begin{array}{rrrrrrr}
\\ \\ \\ \\ \\
6x&-&5&-&30x&>&67 \\
&+&5&&&&+5 \\
\hline
&&&&\dfrac{-24x}{-24}&>&\dfrac{72}{-24} \\ \\
&&&&x&<&-3
\end{array}\)
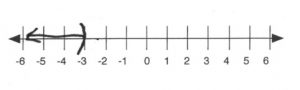
- \(\begin{array}{rrrcrrr}
\\ \\ \\ \\ \\
-10&\le &4x&-&2&\le &14 \\
+2&&&+&2&&+2 \\
\hline
\dfrac{-8}{4}&\le &&\dfrac{4x}{4}&&\le &\dfrac{16}{4} \\ \\
-2&\le &&x&&\le &4
\end{array}\)
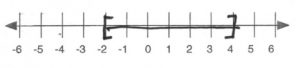
- \(\begin{array}{ll}
\begin{array}{rrl}
\dfrac{3x+2}{5}&=& 2 \\ \\
3x+2&=&10 \\
-2&&-2 \\
\hline
\dfrac{3x}{3}&=&\dfrac{8}{3} \\ \\
x&=&\dfrac{8}{3}
\end{array}
& \hspace{0.25in}
\begin{array}{rrl}
\dfrac{3x+2}{5}&=& -2 \\ \\
3x+2 &=&-10 \\
-2&&-2 \\
\hline
\dfrac{3x}{3}&=&\dfrac{-12}{3} \\ \\
x&=&-4
\end{array}
\end{array}\)
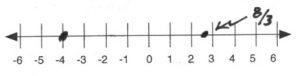
-
\(5x+2y<15\) \(x\) \(y\) 0 7.5 3 0 1 5 5 −5 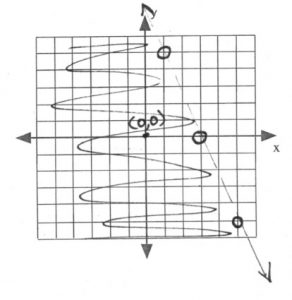
- \(\begin{array}{rrrrrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&(5L&+&3S&=&47)(2) \\
&(4L&-&2S&=&20)(3) \\ \\
&10L&+&6S&=&94 \\
+&12L&-&6S&=&60 \\
\hline
&&&\dfrac{22L}{22}&=&\dfrac{154}{22} \\ \\
&&&L&=&7 \\ \\
\therefore &4L&-&2S&=&\phantom{-}20 \\
&4(7)&-&2S&=&\phantom{-}20 \\
&28&-&2S&=&\phantom{-}20 \\
-&28&&&&-28 \\
\hline
&&&\dfrac{-2S}{-2}&=&\dfrac{-8}{-2} \\ \\
&&&S&=&4
\end{array}\) - \(\begin{array}{rrl}
\\ \\ \\ \\ \\ \\
36\text{ cm}&=&5x+x \\
36\text{ cm}&=&6x \\ \\
x&=&\dfrac{36\text{ cm}}{6} \\ \\
x&=&6\text{ cm} \\
5x&=&5(6)=30 \text{ cm}
\end{array}\) - \[
\begin{aligned}
\text{1st:} \quad y &= \frac{k m n}{d^2} \\[2mm]
\text{2nd:} \quad
y &= 3 \\
k &= \text{find} \\
m &= 2 \\
n &= 8 \\
d &= 4 \\
y &= \frac{k m n}{d^2} \\
3 &= \frac{k \cdot 2 \cdot 8}{4^2} \\
k &= \frac{3 \cdot 16}{16} \\
k &= 3
\end{aligned}
\quad\quad
\begin{aligned}
\text{3rd:} \quad
y &= \text{find} \\
k &= 3 \\
m &= 15 \\
n &= 10 \\
d &= 5 \\
y &= \frac{k m n}{d^2} \\
y &= \frac{3 \cdot 15 \cdot 10}{5^2} \\
y &= 18
\end{aligned}
\]

