Answer Key 4.5
- \(L=2W-3 \text{ and } P=2L+2W \Rightarrow 54=2(2W-3)+2W\)
- \(L=2W-8 \text{ and } P=2L+2W \Rightarrow 64=2(2W-8)+2W\)
- \(L=2W+4 \text{ and } P=2L+2W \Rightarrow 32=2(2W+4)+2W\)
- \(A_1=2A_2, A_1=10^{\circ}+A_3, A_1+A_2+A_3=180^{\circ} \Rightarrow\)
\(A_1+\dfrac{A_1}{2}+A_1- 10^{\circ}=180^{\circ}\) - \(A_1=\dfrac{1}{2}A_2, A_1=20^{\circ}+A_3, A_1+A_2+A_3=180^{\circ} \Rightarrow\)
\(A_1+2A_1+A_1-20^{\circ}=180^{\circ}\) - \(A_1+A_2=\dfrac{1}{2}A_3, A_1+A_2+A_3=180^{\circ} \Rightarrow\)
\(\dfrac{3}{2}A_3=180^{\circ}\hspace{0.34in} A_1 \text{ and } A_2?\) - \(x_1+x_2=140, x_1=5x_2 \Rightarrow 5x_2+x_2=140\)
- \(x_1+x_2=48, x_2=5+x_1 \Rightarrow x_1+5+x_1=48\)
- \(\begin{array}{rrrrrrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
A_2&=&A_1&&&&&&&&&& \\
A_3&=&A_1&+&12&&&&&&&& \\ \\
A_1&+&A_2&+&A_3&&&=&180&&&& \\
A_1&+&A_1&+&A_1&+&12&=&180&&&& \\
&&&&&-&12&&-12&&&& \\
\hline
&&&&&&3A_1&=&168&&&& \\ \\
&&&&&&A_1&=&\dfrac{168}{3}&=&56&& \\
A_1&=&56^{\circ}&&&&&&&&&& \\
A_2&=&56^{\circ}&&&&&&&&&& \\
A_3&=&56^{\circ}&+&12^{\circ}&=&68^{\circ}&&&&&&
\end{array}\) - \(\begin{array}{rrrrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
A_1&=&A_2&&&&&&&& \\
A_3&=&A_1&-&12&&&&&& \\ \\
A_1&+&A_2&+&A_3&&&=&180&& \\
A_1&+&A_1&+&A_1&-&12&=&180&& \\
&&&&&+&12&&+12&& \\
\hline
&&&&&&3A_1&=&192&& \\ \\
&&&&&&A_1&=&\dfrac{192}{3}&=&64 \\
A_1&=&64^{\circ}&&&&&&&& \\
A_2&=&64^{\circ}&&&&&&&& \\
A_3&=&64^{\circ}&-&12^{\circ}&=&52^{\circ}&&&&
\end{array}\) - \(\begin{array}{rrlrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
A_1&=&A_2&&&&&&&& \\
A_3&=&3A_1&&&&&&&& \\ \\
A_1&+&A_2&+&A_3&=&180&&&& \\
A_1&+&A_1&+&3A_1&=&180&&&& \\
&&&&5A_1&=&180&&&& \\ \\
&&&&A_1&=&\dfrac{180}{5}&=&36&& \\
A_1&=&36^{\circ}&&&&&&&& \\
A_2&=&36^{\circ}&&&&&&&& \\
A_3&=&3(36^{\circ})&=&108^{\circ}&&&&&&
\end{array}\) - \(\begin{array}{rrrcrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
A_2&=&2A_1&&&&&&&& \\
A_3&=&A_1&+&20&&&&&& \\ \\
A_1&+&A_2&+&A_3&&&=&180&& \\
A_1&+&2A_1&+&A_1&+&20&=&180&& \\
&&&&&-&20&=&-20&& \\
\hline
&&&&&&4A_1&=&160&& \\ \\
&&&&&&A_1&=&\dfrac{160}{4}&=&40 \\
A_1&=&40^{\circ}&&&&&&&& \\
A_2&=&2(40^{\circ})&=&80^{\circ}&&&&&& \\
A_3&=&20^{\circ}&+&40^{\circ}&=&60^{\circ}&&&&
\end{array}\) - \(\begin{array}{rrlllrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
^{\text{1}}L&=&W&+&15&& \\ \\
^{\text{2}}P&=&2L&+&2W&& \\
150&=&2(W&+&15)&+&2W \\
150&=&2W&+&30&+&2W \\
-30&&&-&30&& \\
\hline
120&=&4W&&&& \\ \\
W&=&\dfrac{120}{4}&=&30\text{ cm}&& \\ \\
^{\text{3}}L&=&30&+&15&& \\
L&=&45\text{ cm}&&&& \\
\end{array}\) - \(\begin{array}{rrlllrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
^{\text{1}}L&=&W&+&40&& \\ \\
^{\text{2}}P&=&2L&+&2W&& \\
304&=&2(W&+&40)&+&2W \\
304&=&2W&+&80&+&2W \\
-80&&&-&80&& \\
\hline
224&=&4W&&&& \\ \\
W&=&\dfrac{224}{4}&=&56\text{ cm}&& \\ \\
^{\text{3}}L&=&56&+&40&& \\
L&=&96\text{ cm}&&&& \\
\end{array}\) - \(\begin{array}{rrlllrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
^{\text{1}}W&=&L&-&22&& \\ \\
^{\text{2}}P&=&2L&+&2W&& \\
152&=&2L&+&2(L&-&22) \\
152&=&2L&+&2L&-&44 \\
+44&&&&&+&44 \\
\hline
196&=&4L&&&& \\ \\
L&=&\dfrac{196}{4}&=&49\text{ m}&& \\ \\
^{\text{3}}W&=&49&-&22&& \\
L&=&27\text{ m}&&&& \\
\end{array}\) - \(\begin{array}{rrlllrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
^{\text{1}}W&=&L&-&26&& \\ \\
^{\text{2}}P&=&2L&+&2W&& \\
280&=&2L&+&2(L&-&26) \\
280&=&2L&+&2L&-&52 \\
+52&&&&&+&52 \\
\hline
332&=&4L&&&& \\ \\
L&=&\dfrac{332}{4}&=&83\text{ m}&& \\ \\
^{\text{3}}W&=&83&-&26&& \\
L&=&57\text{ m}&&&& \\
\end{array}\) - \(\begin{array}{rrrrrrrr}
\\ \\ \\ \\ \\
x&+&2x&=&12&&& \\
&&3x&=&12&&& \\ \\
&&x&=&\dfrac{12}{3}&=&4\text{ cm}& \\ \\
&\therefore &2x&=&2(4)&=&8\text{ cm}& \\
\end{array}\)\(\text{Pieces are 4 cm and 8 cm}\)
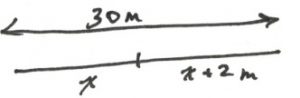
- \(\begin{array}{rrrrrrrrcrr}
\\ \\ \\ \\ \\ \\ \\
x&+&x&+&2&=&30&&&& \\
&&&-&2&&-2&&&& \\
\hline
&&&&2x&=&28&&&& \\ \\
&&&&x&=&\dfrac{28}{2}&=&14\text{ m}&& \\ \\
&\therefore &x&+&2&=&14&+&2&=&16 \text{ m}
\end{array}\)\(\text{Pieces are 14 m and 16 m}\)