"

Answer Key 4.3

  1. \(\begin{array}{rrcrrr}
    -3& <& x& <& 3& \hspace{0.25in} \text{Interval notation: } (-3,3)
    \end{array}\) (-3,3)
  2. \(\begin{array}{rrcrrr}
    -8& \le& x& \le& 8 & \hspace{0.25in} \text{Interval notation: } [-8,8]
    \end{array}\) Numberline (-3,3)
  3. \(\begin{array}{rrcrrr}
    \\ \\ \\
    \dfrac{-6}{2}&<&\dfrac{2x}{2}&<&\dfrac{6}{2}& \\ \\
    -3&<&x&<&3& \hspace{0.25in} \text{Interval notation: } (-3,3)
    \end{array}\) Numerline (-8,8)
  4. \(\begin{array}{rrrcrrrr}
    \\ \\
    -4&<&x&+&3&<&4& \\
    -3&&&-&3&&-3& \\
    \hline
    -7&<&&x&&<&1& \hspace{0.25in} \text{Interval notation: } (-7,1)
    \end{array}\)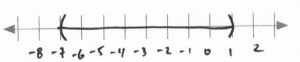 Numberline (-7,1)
  5. \(\begin{array}{rrrcrrrr}
    \\ \\
    -6&<&x&-&2&<&6& \\
    +2&&&+&2&&+2& \\
    \hline
    -4&<&&x&&<&8& \hspace{0.25in} \text{Interval notation: } (-4,8)
    \end{array}\) Numberline (-4,8)
  6. \(\begin{array}{rrrcrrrr}
    \\ \\
    -12&<&x&-&8&<&12& \\
    +8&&&+&8&&+8& \\
    \hline
    -4&<&&x&&<&20& \hspace{0.25in} \text{Interval notation: } (-4,20)
    \end{array}\) Numberline (-4, 20)
  7. \(\begin{array}{rrrcrrrr}
    \\ \\
    -3&<&x&-&7&<&3& \\
    +7&&&+&7&&+7& \\
    \hline
    4&<&&x&&<&10& \hspace{0.25in} \text{Interval notation: } (4,10)
    \end{array}\)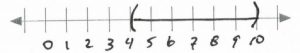 Numberline (4,10)
  8. \(\begin{array}{rrrcrrrr}
    \\ \\
    -4&\le &x&+&3&\le &4& \\
    -3&&&-&3&&-3& \\
    \hline
    -7&\le &&x&&\le &1& \hspace{0.25in} \text{Interval notation: } [-7,1]
    \end{array}\)  Numberline (-9, 1)
  9. \(\begin{array}{rrrcrrrr}
    \\ \\ \\ \\ \\
    -9&<&3x&-&2&<&9& \\
    +2&&&+&2&&+2& \\
    \hline
    \dfrac{-7}{3}&<&&\dfrac{3x}{3}&&<&\dfrac{11}{3}&\\ \\
    -\dfrac{7}{3}&<&&x&&<&\dfrac{11}{3}& \hspace{0.25in} \text{Interval notation: } (-\dfrac{7}{3},\dfrac{11}{3})
    \end{array}\)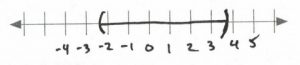  Numberline (-2.25, 3.75)
  10. \(\begin{array}{rrrcrrrr}
    \\ \\ \\ \\ \\
    -9&<&2x&+&5&<&9& \\
    -5&&&-&5&&-5& \\
    \hline
    \dfrac{-14}{2}&<&&\dfrac{2x}{2}&&<&\dfrac{4}{2}&\\ \\
    -7&<&&x&&<&2& \hspace{0.25in} \text{Interval notation: } (-7,2)
    \end{array}\) Numberline (-7,2)
  11. \(\begin{array}{rrrcrrrr}
    \\ \\ \\ \\ \\ \\ \\ \\
    1&+&2|x&-&1|&\le & 9 \\
    -1&&&&&&-1 \\
    \hline
    &&\dfrac{2}{2}|x&-&1|&\le & \dfrac{8}{2} \\ \\
    &&|x&-&1|&\le & 4 \\
    -4&\le &x&-&1&\le & 4 \\
    +1&&&+&1&\le &+1 \\
    \hline
    -3&\le &&x&&\le &5& \hspace{0.25in} \text{Interval notation: } [-3,5]
    \end{array}\) Numberline (-3,5)
  12. \(\begin{array}{rrrcrrrr}
    \\ \\ \\ \\ \\ \\ \\ \\
    10&-&3|x&-&2|&\ge & 4 \\
    -10&&&&&&-10 \\
    \hline
    &&\dfrac{-3}{-3}|x&-&2|&\ge & \dfrac{-6}{-3} \\ \\
    &&|x&-&2|&\le & 2 \\
    -2&\le &x&-&2&\le & 2 \\
    +2&&&+&2&&+2 \\
    \hline
    0&\le &&x&&\le &4& \hspace{0.25in} \text{Interval notation: } [0,4]
    \end{array}\)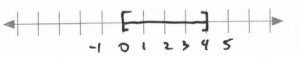 Numberline (0,4)
  13. \(\begin{array}{rrrcrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\
    6&-&|2x&-&5|&>&3& \\
    -6&&&&&&-6& \\
    \hline
    &&(-|2x&-&5|&>&-3)&(-1) \\
    &&|2x&-&5|&<&3& \\
    -3&<&2x&-&5&<&3& \\
    +5&&&+&5&&+5& \\
    \hline
    \dfrac{2}{2}&<&&\dfrac{2x}{2}&&<&\dfrac{8}{2}& \\ \\
    1&<&&x&&<&4& \hspace{0.25in} \text{Interval notation: } (1,4)&
    \end{array}\) Numberline (1,4)
  14. \(\begin{array}{rrcrrrrrr}
    x& <&-5&\text{or}&5&<&x& \hspace{0.25in} \text{Interval notation: } (-\infty,-5)\cup (5, \infty)
    \end{array}\) Numberline (- infinity, -5) or (5, infinity)
  15. \(\begin{array}{rrrrrrrr}
    \\ \\ \\
    \dfrac{3x}{3}&<&\dfrac{-5}{3}&\text{or}&\dfrac{5}{3}&<&\dfrac{3x}{3}& \\ \\
    x&<&-\dfrac{5}{3}&\text{or}&\dfrac{5}{3}&<&x&\text{Interval notation: } (-\infty, -\dfrac{5}{3})\cup (\dfrac{5}{3}, \infty) \\
    \end{array}\)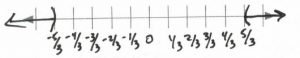 (- infinity, -5/3) or (5/3, infinity)
  16. \(\begin{array}{rrrrrrrrrrrr}
    \\ \\
    x&-&4&<&-5&\text{or}&5&<&x&-&4& \\
    &+&4&&+4&\text{or}&+4&&&+&4& \\
    \hline
    &&x&<&-1&\text{or}&9&<&x&&&\text{Interval notation: } (-\infty, -1)\cup (9, \infty)\\
    \end{array}\)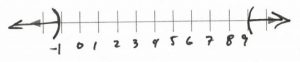 (- infinity, -1) or (9, infinity)
  17. \(\begin{array}{rrrrrrrrrrrr}
    \\ \\
    x&+&3&<&-3&\text{or}&3&<&x&+&3& \\
    &-&3&&-3&\text{or}&-3&&&-&3& \\
    \hline
    &&x&<&-6&\text{or}&0&<&x&&&\text{Interval notation: } (-\infty, -6)\cup (0, \infty)\\
    \end{array}\) (- infinity, -6) or (0, infinity)
  18. \(\begin{array}{rrrrrrrrrrrr}
    \\ \\ \\ \\
    2x&-&4&<&-6&\text{or}&6&<&2x&-&4& \\
    &+&4&&+4&&+4&&&+&4& \\
    \hline
    &&\dfrac{2x}{2}&<&\dfrac{-2}{2}&&\dfrac{10}{2}&<&\dfrac{2x}{2}&&& \\ \\
    &&x&<&-1&\text{or}&5&<&x&&&\text{Interval notation: } (-\infty, -1)\cup (5, \infty)\\
    \end{array}\) (negative infinity, -1) or (5, infinity)
  19. \(\begin{array}{rrrrrrrrrrrr}
    \\ \\ \\
    x&-&5&<&-3&\text{or}&3&<&x&-&5& \\
    &+&5&&+5&&+5&&&+&5& \\
    \hline
    &&x&<&2&\text{or}&8&<&x&&&\text{Interval notation: } (-\infty, 2)\cup (8, \infty)\\
    \end{array}\)  HAVE TO ADD 2   2  etc.
     (1, negative infinity) or (4, infinity)
  20. \(\begin{array}{rrrrrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\
    3&-|2&-&x|&<&1&&&&&\\
    -3&&&&&-3&&&&&\\
    \hline
    &(-|2&-&x|&<&-2)&(-1)&&&&\\
    &|2&-&x|&>&2&&&&&\\ \\
    2&-&x&<&-2&\text{or}&2&<&2&-&x\\
    -2&&&&-2&&-2&&-2&&\\
    \hline
    &&-x&<&-4&\text{or}&0&<&-x&&\\
    &&x&>&4&\text{or}&0&>&x&&\text{Interval notation: } (-\infty, 0)\cup (4, \infty)\\
    \end{array}\)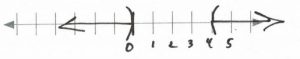 (negative infinty, 0) or (4, infinity)
  21. \(\begin{array}{rrrrrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\
    4&+&3|x&-&1|&<&10&&&&\\
    -4&&&&&&-4&&&&\\
    \hline
    &&\dfrac{3}{3}|x&-&1|&<&\dfrac{6}{3}&&&&\\ \\
    &&|x&-&1|&<&2&&&&\\ \\
    x&-&1&<&-2&\text{or}&2&<&x&-&1\\
    &+&1&&+1&&+1&&&+&1\\
    \hline
    &&x&<&-1&\text{or}&3&<&x&&\text{Interval notation: } (-\infty, -1)\cup (3, \infty)\\
    \end{array}\) (negative infinity, -1) or (3, infinity)
  22. \(\begin{array}{rrrcrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    3&-&2|3x&-&1|&\ge &-7& \\
    -3&&&&&&-3& \\
    \hline
    &&\dfrac{-2}{-2}|3x&-&1|&\ge &\dfrac{-10}{-2}& \\ \\
    &&|3x&-&1|&\le &5& \\ \\ \\
    -5&\le &3x&-&1& \le & 5& \\
    +1&&&+&1&&+1& \\
    \hline
    \dfrac{-4}{3}&\le &&\dfrac{3x}{3}&& \le & \dfrac{6}{3}& \\ \\
    -\dfrac{4}{3}&\le &&x&& \le & 2 &\text{Interval notation: } [-\dfrac{4}{3}, 2]
    \end{array}\)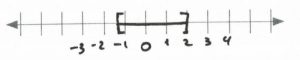 (-4/3, 2)
  23. \(\begin{array}{rrrrrcrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\
    3&-&2|x&-&5|&\le & -15&&&& \\
    -3&&&&&&-3&&&& \\
    \hline
    &&\dfrac{-2}{-2}|x&-&5|&\le & \dfrac{-18}{-2}&&&& \\ \\
    &&|x&-&5|&\ge & 9&&&& \\ \\
    x&-&5&\le &-9&\text{or}&9&\le &x&-&5 \\
    &+&5&&+5&&+5&&&+&5 \\
    \hline
    &&x&\le &-4&\text{or}&14&\le &x&&\text{Interval notation: } (-\infty, -4]\cup [14, \infty)
    \end{array}\) (- ifninity, -4] or [14, infinity)
  24. \(\begin{array}{rrcrrcrrrll}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    4&-&6|-6&-&3x|&\le & -5&&&& \\
    -4&&&&&&-4&&&& \\
    \hline
    &&\dfrac{-6}{-6}|-6&-&3x|&\le &\dfrac{-9}{-6}&&&& \\ \\
    &&|-6&-&3x|&\ge &\dfrac{3}{2}&&&& \\ \\ \\
    -6&-&3x&\le &-\dfrac{3}{2}&\text{or}&\dfrac{3}{2}&\le &-6&-\phantom{0}3x& \\ \\
    +6&&&&+6&&+6&&+6&& \\
    \hline
    &&\dfrac{-3x}{-3}&\le &\dfrac{\dfrac{9}{2}}{-3}&&\dfrac{\dfrac{15}{2}}{-3}&\le &\dfrac{-3x}{-3}&& \\ \\
    &&x&\ge &-\dfrac{3}{2}&\text{or}&-\dfrac{5}{2}&\ge &x&\text{Interval notation: } (-\infty, -\dfrac{5}{2}]\cup [-\dfrac{3}{2}, \infty)& \\
    \end{array}\)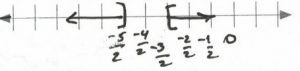 [-5/2, negative infinty) or [-2/3, infinity)
  25. \(\begin{array}{rrrcrrrr}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    -2&-&3|4&-&2x|&\ge & -8& \\
    +2&&&&&&+2& \\
    \hline
    &&\dfrac{-3}{-3}|4&-&2x|&\ge &\dfrac{-6}{-3}& \\ \\
    &&|4&-&2x|&\le &2& \\ \\ \\
    -2&\le &4&-&2x&\le &2& \\
    -4&&-4&&&&-4& \\
    \hline
    \dfrac{-6}{-2}&\le &&\dfrac{-2x}{-2}&&\le &\dfrac{-2}{-2}& \\ \\
    3&\ge &&x&&\ge &1&\text{Interval notation: } [1,3]
    \end{array}\) [1,3]
  26. \(\begin{array}{rrrcrcrr}
    \\ \\ \\ \\ \\ \\ \\
    -3&-&2|4x&-&5|&\ge & 1& \\
    +3&&&&&&+3& \\
    \hline
    &&\dfrac{-2}{-2}|4x&-&5|&\ge &\dfrac{4}{-2}& \\ \\
    &&|4x&-&5|&\le &-2& \\ \\
    &&&&&\uparrow&& \\
    &&&&&\text{Cannot be true.}&&\text{No solution.} \\
    \end{array}\) Numerline no solution
  27. \(\begin{array}{rrrrrrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\
    4&-&5|-2x&-&7|&<&-1&&&&& \\
    -4&&&&&&-4&&&&& \\
    \hline
    &&\dfrac{-5}{-5}|-2x&-&7|&<&\dfrac{-5}{-5}&&&&& \\ \\
    &&|-2x&-&7|&>&1&&&&& \\ \\ \\
    -2x&-&7&<&-1&\text{or}&1&<&-2x&-&7& \\
    &+&7&&+7&&+7&&&+&7& \\
    \hline
    &&\dfrac{-2x}{-2}&<&\dfrac{6}{-2}&&\dfrac{8}{-2}&<&\dfrac{-2x}{-2}&&& \\ \\
    &&x&>&-3&\text{or}&-4&>&x&&&\text{Interval notation: } (-\infty, -4)\cup (-3, \infty)
    \end{array}\)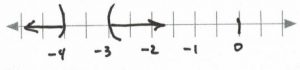 (negative infinity, -4) or (-3, infinity)
  28. \(\begin{array}{rrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    -2&+&3|5&-&x|& \le& 4& \\
    +2&&&&&&+2& \\
    \hline
    &&\dfrac{3}{3}|5&-&x|& \le&\dfrac{6}{3}& \\ \\
    &&|5&-&x|& \le&2& \\ \\
    -2&\le &5&-&x&\le &2& \\
    -5&&-5&&&&-5& \\
    \hline
    (-7&\le &&-x&&\le &-3)&(-1) \\
    7&\ge &&x&&\ge &3&\text{Interval notation: } [3,7]\\
    \end{array}\) [3,7]
  29. \(\begin{array}{rrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    3&-&2|4x&-&5|&\ge &1& \\
    -3&&&&&&-3& \\
    \hline
    &&\dfrac{-2}{-2}|4x&-&5|&\ge &\dfrac{-2}{-2}& \\ \\
    &&|4x&-&5|&\le &1& \\ \\
    -1&\le &4x&-&5&\le &1& \\
    +5&&&+&5&&+5& \\
    \hline
    \dfrac{4}{4}&\le &&\dfrac{4x}{4}&&\le &\dfrac{6}{4}& \\ \\
    1&\le &&x&&\le &\dfrac{3}{2}&\text{Interval notation: } [1, \dfrac{3}{2}]
    \end{array}\) [2/2, 3/2]
  30. \(\begin{array}{rrrcrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    -2&-&3|-3x&-&5|&\ge &-5& \\
    +2&&&&&&+2& \\
    \hline
    &&\dfrac{-3}{-3}|-3x&-&5|&\ge &\dfrac{-3}{-3}& \\ \\
    &&|-3x&-&5|&\le &1& \\ \\
    -1&\le &-3x&-&5&\le &1& \\
    +5&&&+&5&&+5& \\
    \hline
    \dfrac{4}{-3}&\le &&\dfrac{-3x}{-3}&&\le &\dfrac{6}{-3}& \\ \\
    -\dfrac{4}{3}&\ge &&x&&\ge &-2&\text{Interval notation: } [-2, -\dfrac{4}{3}]
    \end{array}\) [-6/3, -4/3]
  31. \(\begin{array}{rrrrrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    -5&-&2|3x&-&6|&<&-8&&&& \\
    +5&&&&&&+5&&&& \\
    \hline
    &&\dfrac{-2}{-2}|3x&-&6|&<&\dfrac{-3}{-2}&&&& \\ \\
    &&|3x&-&6|&>&\dfrac{3}{2}&&&& \\ \\ \\
    3x&-&6&<&-\dfrac{3}{2}&\text{or}&\dfrac{3}{2}&<&3x&-&6 \\ \\
    &+&6&&+6&&+6&&&+&6 \\
    \hline
    &&\dfrac{3x}{3}&<&\dfrac{\dfrac{9}{2}}{3}&&\dfrac{\dfrac{15}{2}}{3}&<&\dfrac{3x}{3}&& \\ \\
    &&x&<&\dfrac{3}{2}&\text{or}&5&<&x&&\text{Interval notation: } (-\infty, \dfrac{3}{2})\cup (5, \infty)
    \end{array}\)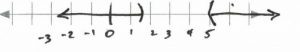 (negative infinity, -1/2) or (5, infinity)
  32. \(\begin{array}{rrrrrrrrrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\
    6&-&3|1&-&4x|&<&-3&&&&& \\
    -6&&&&&&-6&&&&& \\
    \hline
    &&\dfrac{-3}{-3}|1&-&4x|&<&\dfrac{-9}{-3}&&&&& \\ \\
    &&|1&-&4x|&>&3&&&&& \\ \\
    1&-&4x&<&-3&\text{or}&1&-&4x&>&3& \\
    -1&&&&-1&&-1&&&&-1& \\
    \hline
    &&-4x&<&-4&&&&-4x&>&2& \\
    &&x&>&1&&\text{or}&&x&<&-\dfrac{1}{2}&\text{Interval notation: } (-\infty, -\dfrac{1}{2})\cup (1, \infty)
    \end{array}\)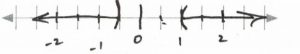 (negative infinity, -1/2) or (1, infinity)
  33. \(\begin{array}{rrrcrrrl}
    \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
    4&-&4|-2x&+&6|&>&-4& \\
    -4&&&&&&-4& \\
    \hline
    &&\dfrac{-4}{-4}|-2x&+&6|&>&\dfrac{-8}{-4}& \\ \\
    &&|-2x&+&6|&<&2& \\ \\
    -2&<&-2x&+&6&<&2& \\
    -6&&&-&6&&-6& \\
    \hline
    \dfrac{-8}{-2}&<&&\dfrac{-2x}{-2}&&<&\dfrac{-4}{-2}& \\ \\
    4&>&&x&&>&2&\text{Interval notation: } (2,4)
    \end{array}\) (2,4)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book