Midterm 2: Prep Answer Key
[latexpage]
Midterm Two Review
-
\(x-2y=-4\) \(x\) \(y\) −4 0 0 2 −2 1 \(x+y=5\) \(x\) \(y\) 0 5 5 0 2 3 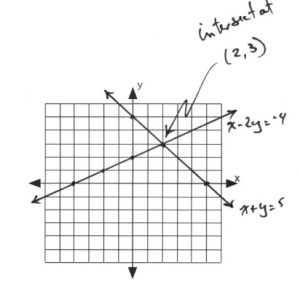
- \(\begin{array}{rrcrlrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\
2x&-&y&=&0&\Rightarrow &y=2x \\
3x&+&4y&=&-22&& \\ \\
\therefore 3x&+&4(2x)&=&-22&& \\
3x&+&8x&=&-22&& \\
&&11x&=&-22&& \\
&&x&=&-2&& \\ \\
&&y&=&2x&& \\
&&y&=&2(-2)&=&-4 \\
\end{array}\)
\((-2,-4)\) - \(\begin{array}{rrrrrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&(2x&-&5y&=&15)(2) \\
&(3x&+&2y&=&13)(5) \\
\midrule
&4x&-&10y&=&30 \\
+&15x&+&10y&=&65 \\
\midrule
&&&19x&=&95 \\
&&&x&=&5 \\ \\
&\therefore 3(5)&+&2y&=&\phantom{-}13 \\
&15&+&2y&=&\phantom{-}13 \\
&-15&&&&-15 \\
\midrule
&&&2y&=&-2 \\
&&&y&=&-1
\end{array}\)
\((5,-1)\) - \(\begin{array}{rr}
\begin{array}{rrrrrrrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&&&(5x&+&6z&=&-4)(-1) \\ \\
&5x&+&y&+&6z&=&-2 \\
+&-5x&&&-&6z&=&\phantom{-}4 \\
\midrule
&&&&&y&=&2 \\ \\
&&&\therefore 2y&-&3z&=&\phantom{-}3 \\
&&&2(2)&-&3z&=&\phantom{-}3 \\
&&&-4&&&&-4 \\
\midrule
&&&&&-3z&=&-1 \\
&&&&&z&=&\dfrac{1}{3} \\
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrr}
\\ \\ \\ \\ \\ \\
5x&+&6z&=&-4 \\
5x&+&6\left(\dfrac{1}{3}\right)&=&-4 \\
5x&+&2&=&-4 \\
&-&2&&-2 \\
\midrule
&&5x&=&-6 \\
&&x&=&-\dfrac{6}{5}
\end{array}
\end{array}\)
\(-\dfrac{6}{5}, 2, \dfrac{1}{3}\) - \(\begin{array}{rrrrrr}
\\ \\ \\
&4a^2&-&9a&+&2 \\
&-a^2&+&4a&+&5 \\
+&3a^2&-&a&+&9 \\
\midrule
&6a^2&-&6a&+&16
\end{array}\) - \(8x^4-12x^2y^2-15x^2y^2-3x^4\Rightarrow 5x^4-27x^2y^2\)
- \(\begin{array}{l}
\\ \\ \\
6-2\left[3x-20x+8-1\right] \\
6-2\left[-17x+7\right] \\
6+34x-14 \\
34x-8
\end{array}\) - \(25a^{-10}b^6\text{ or } \dfrac{25b^6}{a^{10}}\)
- \(\begin{array}{l}
\\
8a^2(a^2+10a+25) \\
8a^4+80a^3+200a^2
\end{array}\) - \(\begin{array}{l}
\\
4ab^2(a^2-4) \\
4a^3b^2-16ab^2
\end{array}\) - \(\begin{array}{rrrrrrrr}
\\ \\ \\ \\ \\
&x^2&-&4x&+&7\phantom{x}&& \\
\times &&&x&-&3\phantom{x}&& \\
\midrule
&x^3&-&4x^2&+&7x&& \\
+&&-&3x^2&+&12x&-&21 \\
\midrule
&x^3&-&7x^2&+&19x&-&21 \\
\end{array}\) - \(\begin{array}{rrrrrrrrrr}
\\ \\ \\ \\ \\ \\
&2x^2&+&x&-&3\phantom{x^2}&&&& \\
\times &2x^2&+&x&-&3\phantom{x^2}&&&& \\
\midrule
&4x^4&+&2x^3&-&6x^2&&&& \\
&&&2x^3&+&x^2&-&3x&& \\
+&&&&&-6x^2&-&3x&+&9 \\
\midrule
&4x^4&+&4x^3&-&11x^2&-&6x&+&9
\end{array}\) - \(\begin{array}{rrrrrrrrrr}
\\ \\ \\ \\ \\ \\
&x^2&+&5x&-&2\phantom{x^2}&&&& \\
\times &2x^2&-&x&+&3\phantom{x^2}&&&& \\
\midrule
&2x^4&+&10x^3&-&4x^2&&&& \\
&&&-x^3&-&5x^2&+&2x&& \\
+&&&&&3x^2&+&15x&-&6 \\
\midrule
&2x^4&+&9x^3&-&6x^2&+&17x&-&6
\end{array}\) - \(\begin{array}{rrrrrrrrrr}
\\ \\ \\ \\ \\
(x+4)(x+4)&\Rightarrow &&x^2&+&8x&+&16&& \\
&&\times&&&x&+&4&& \\
\midrule
&&&x^3&+&8x^2&+&16x&& \\
&&+&&&4x^2&+&32x&+&64 \\
\midrule
&&&x^3&+&12x^2&+&48x&+&64
\end{array}\) - \(r^{-4-3}s^{9+9}\Rightarrow r^{-7}s^{18}\Rightarrow \dfrac{s^{18}}{r^7}\)
\(\dfrac{s^{18}}{r^7}\) - \(\begin{array}{l}
\\ \\
(x^{-2--2}y^{-3-4})^{-1} \\
(1\cancel{x^0}y^{-7})^{-1} \\
y^7
y^7
\end{array}\) - \(\polylongdiv{2x^3-7x^2+15}{x-2}\)
- \(2^3\cdot 11\)
- \(2^5\cdot 3\cdot 7
\left\{
\begin{array}{l}
84=2^2\cdot 3\cdot 7 \\
96=2^5\cdot 3
\end{array}\right.\) - \(x(5y+6z)-3(5y+6z)\)
\((5y+6z)(x-3)\) - \(-12=4\times -3\)
\(1=4+-3 \\ \)
\(x^2+4x-3x-12\)
\(x(x+4)-3(x+4)\)
\((x+4)(x-3)\) - \(x^2(x+1)-4(x+1)\)
\((x+1)(x^2-4)\)
\(x+1)(x-2)(x+2) - \(x^3-(3y)^3\)
\((x-3y)(x^2+3xy+9y^2)\) - \((x^2-36)(x^2+1)\)
\((x-6)(x+6)(x^2+1)\) - \(\begin{array}{lll}
\begin{array}{rrrrl}
(A&+&B&=&70)(-4) \\
4A&+&7B&=&430
\end{array}
& \Rightarrow \hspace{0.25in}
\begin{array}{rrrrrl}
\\ \\ \\ \\
&-4A&-&4B&=&-280 \\
+&4A&+&7B&=&\phantom{-}430 \\
\midrule
&&&3B&=&\phantom{-}150 \\ \\
&&&B&=&\dfrac{150}{3}\text{ or }50
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrr}
\\ \\ \\
\therefore A&+&B&=&70 \\ \\
A&+&50&=&70 \\
&&-50&&-50 \\
\midrule
&&A&=&20
\end{array}
\end{array}\) - \(\begin{array}{rrcrrrl}
\\ \\ \\ \\ \\ \\ \\
5x&+&21(2)&=&11(x&+&2) \\ \\
5x&+&42&=&11x&+&22 \\
-5x&-&22&&-5x&-&22 \\
\midrule
&&20&=&6x&& \\ \\
&&x&=&\dfrac{20}{6}&=&3\dfrac{1}{3}\text{ litres} \\
\end{array}\) - \(\phantom{1}\)
\(B+G=16\Rightarrow B=16-G\text{ or }G=16-B \\ \)
\(\begin{array}{ll}
\begin{array}{rrrrrrr}
\\ \\ \\ \\ \\
G&-&4&=&3(B&-&4) \\
16-B&-&4&=&3B&-&12 \\
+B&+&12&&+B&+&12 \\
\midrule
&&24&=&4B&& \\ \\
&&B&=&\dfrac{24}{4}&=&6
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrr}
\\
\therefore G&=&16&-&B \\
G&=&16&-&6 \\
G&=&10&&
\end{array}
\end{array}\)

