Mid Term 1: Review Questions Answer Key
- True
- Undefined
- 15
- 16
- 12
- 19
- True
- −18
- 18
- −16
- 16
- −16
- \(\begin{array}{l}
\\ \\ \\
-(-6) - \sqrt{(-6)^2-4(8)(-2)} \\
6 - \sqrt{36+64} \\
6-10 \\
-4
\end{array}\) - \(\begin{array}{rrrrrrrrrrrr}
\\ \\ \\ \\ \\
&3x&-&12&-&27&=&7&-&5x&-&30 \\
+&5x&+&12&+&27&&&+&5x&+&12 \\
&&&&&&&&&&+&7 \\
&&&&&&&&&&+&27 \\
\hline
&&&&&8x&=&16&&&& \\
&&&&&x&=&2&&&&
\end{array}\) - \(\begin{array}{l}
\\ \\ \\ \\ \\ \\ \\
\left(\dfrac{1}{R} = \dfrac{1}{r_1}+\dfrac{1}{r_2}\right)(Rr_1r_2) \\ \\
r_1r_2 = Rr_2 + Rr_1 \\ \\
r_1r_2 = R(r_2 + r_1) \\ \\
R=\dfrac{r_1r_2}{r_2 + r_1}
\end{array}\) - \(\phantom{1}\)
\(\left(\dfrac{x+3}{8} - \dfrac{3}{4} = \dfrac {x+6}{10}\right)(40) \\ \)
\(\begin{array}{rrrrrcrrrr}
&5(x&+&3)&-&3(10)&=&4(x&+&6) \\
&5x&+&15&-&30&=&4x&+&24 \\
-&4x&-&15&+&30&&-4x&-&15 \\
&&&&&&&&+&30 \\
\hline
&&&&&x&=&39&&
\end{array}\) - Need graph drawn. \(y=5\)
- \(\begin{array}{ll}
\begin{array}{rrl}
\\ \\
m&=&\dfrac {\Delta y}{\Delta x}\\ \\
\dfrac{2}{3}& =& \dfrac{y-2}{x- -1}
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrrrrcl}
\\ \\ \\ \\ \\
&&2(x&+&1)& =& 3(y&-&2) \\
&&2x &+& 2& = &3y& -& 6 \\
&&-3y& + &6 &&-3y &+ &6 \\
\hline
2x&-&3y&+&8&=&0&& \\ \\
&&&&y&=&\dfrac{2}{3}x&+&\dfrac{8}{3}
\end{array}
\end{array}\) - \(\begin{array}{ll}
\begin{array}{rrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&& \text{1st slope} \\ \\
m&=&\dfrac{\Delta y}{\Delta x} \\ \\
m&=&\dfrac{11--1}{2--2} \\ \\
m&=&\dfrac{12}{4} \\ \\
m&=& 3 \\ \\
&& \text{2nd slope} \\ \\
m&=&\dfrac{\Delta y}{\Delta x} \\ \\
3&=&\dfrac{y--1}{x--2}
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\
&&3(x&+&2)&=&y&+&1 \\
&&3x&+&6&=&y&+&1 \\
&&-y&-&1&&-y&-&1 \\
\hline
3x&-&y&+&5&=&0&& \\
&&&&y&=&3x&+&5
\end{array}
\end{array}\) -
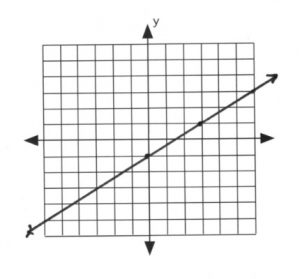
Use slop intercept method. - \(\begin{array}{rrl}
\\ \\ \\
d^2& =& \Delta x^2 + \Delta y^2\\
d^2 &=& (15-7)^2 + (3 - -3)^2\\
d^2& =& 8^2 + 6^2 \\
d&=&10
\end{array}\) - \(\phantom{1}\)
\(x=\dfrac{x_1+x_2}{2}=\dfrac{7+15}{2}=11 \\ \)
\(y=\dfrac{y_1+y_2}{2}=\dfrac{-3+3}{2}=0 \\ \)
\((11,0)\) - True
- True
- \(\{r, s, t\}\)
- True
- \(\begin{array}{rrrrrrr}
\\ \\ \\
3x&-&6&-&36x&>&60 \\
&+&6&&&&+6 \\
\hline
&&&&-33x&>&66 \\
&&&&x&<&-2
\end{array}\)
(−∞, −2) - \(\begin{array}{rrrcrcr}
\\ \\ \\ \\ \\
-18& \le& 4x& - &6& \le& 2\\
+6&&&+&6&&+6\\
\hline
\dfrac{-12}{4}&\le&&\dfrac{4x}{4}&&\le&\dfrac{8}{4}\\ \\
-3&\le&&x&&\le&2
\end{array}\)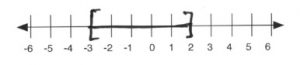
[−3, 2] - \(\begin{array}{ll}
\\ \\ \\ \\ \\
\begin{array}{rrrrr}
2x&-&1&<&-7 \\
&+&1&&+1 \\
\hline
&&\dfrac{2x}{2}&<&\dfrac{-6}{2} \\ \\
&&x&<&-3
\end{array}
& \hspace{0.25in}
\begin{array}{rrrrr}
7&<&2x&-&1 \\
+1&&&+&1 \\
\hline
\dfrac{8}{2}&<&\dfrac{2x}{2}&& \\ \\
4&<&x&&
\end{array}
\end{array}\)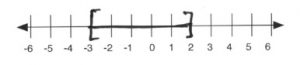
(−∞, −3) or (4, ∞) WRONG IMAGE - \(\phantom{1}\)
\(\left| \dfrac{3x - 4}{5} \right| < 1 \\ \)
\(\left(-1 < \dfrac{3x-4}{5}< 1 \right)(5) \\ \)
\(\begin{array}{rrrrrrr}
-5&<&3x&-&4&<&5 \\
+4&&&+&4&&+4 \\
\hline
\dfrac{-1}{3}&<&&\dfrac{3x}{3}&&<&\dfrac{9}{3} \\ \\
-\dfrac{1}{3}&<&&x&&<&3
\end{array}\)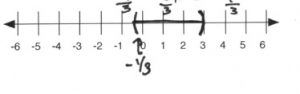
\((-\dfrac{1}{3}, 3)\) - \(\begin{array}{rrrrrrrr}
\\ \\ \\ \\ \\
&3x&-&2y&=&10&& \\
+&-10&+&2y&&-10&+&2y \\
\hline
&\dfrac{3x}{2}&-&\dfrac{10}{2}&=&\dfrac{2y}{2}&& \\ \\
&&&y&=&\dfrac{3}{2}x&-&5
\end{array}\)
Slope intercept method. Check (0, 0): 3(0) − 2(0) < 10. Shade the (0, 0) side. -
\(y=|x-1|-2\) \(x\) \(y\) 4 1 3 0 2 −1 1 −2 0 −1 −1 0 −2 1 - \(\begin{array}{rrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&6L&+&2S&=&38 \\
+&4L&-&2S&=&12 \\
\hline
&&&10L&=&50 \\
&&&L&=&5 \\ \\
\therefore &6(5)&+&2S&=&38 \\
&30&+&2S&=&38 \\
-&30&&&&-30 \\
\hline
&&&2S&=&8 \\
&&&S&=&4
\end{array}\) - Insert diagram.
\(\begin{array}{rrl}
5x+x&=&36 \\
6x&=&36 \\
x&=&6 \\
\therefore 5x&=&30
\end{array}\) - \(\begin{array}{rrrrrl}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
&(d&+&q&=&14)(-10) \\
&10d&+&25q&=&260 \\ \\
&-10d&-&10q&=&-140 \\
+&10d&+&25q&=&\phantom{-}260 \\
\hline
&&&\dfrac{15q}{15}&=&\dfrac{120}{15} \\ \\
&&&q&=&8 \\ \\
\therefore &d&+&8&=&14 \\
&&-&8&&-8 \\
\hline
&&&d&=&6
\end{array}\) - \(\phantom{1}\)
\(x, x+2 \\ \)
\(\begin{array}{rrrrrrrrr}
x&+&x&+&2&=&x&-&10 \\
&&2x&+&2&=&x&-&10 \\
&&-x&-&2&&-x&-&2 \\
\hline
&&&&x&=&-12&& \\
\end{array}\)
\(\phantom{1}\) -
\[
\text{1st: } y = \frac{kmn^2}{d}
\]\[
\text{2nd: }
\begin{aligned}
y &= 12 \\
k &= \text{find} \\
m &= 3 \\
n &= 4 \\
d &= 8 \\[1em]
12 &= \frac{k (3) (4)^2}{8} \\
k &= \frac{12 \cdot 8}{3 \cdot 16} \\
k &= 2
\end{aligned}
\]\[
\text{3rd: }
\begin{aligned}
y &= \text{find} \\
k &= 2 \\
m &= -3 \\
n &= 3 \\
d &= 6 \\[1em]
y &= \frac{(2)(-3)(3)^2}{6} \\
y &= -9
\end{aligned}
\]

