Structure Features of Allyl System

In the structure of allyl carbocation, both double carbons are in sp² hybridization, with an unhybridized 2p orbital perpendicular to the hybrid orbitals as shown in Fig. 3.1a. There is one electron in the 2p orbital for each of the double-bond carbon. The carbon that bears a positive charge is also in sp² hybridization, with the same set of orbitals, however the 2p orbital is empty. So there are a total of two π electrons in allyl carbocation.

When there is at least one atom with p orbital adjacent to at least one π bond, the whole system is a conjugated system. The allyl carbocation, with three p orbitals in total, fits in the definition and is an example of the simplest conjugated system, the allyl system.

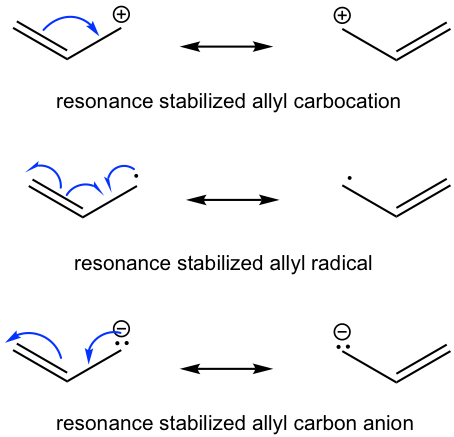
Besides the allyl carbocation, the allyl system also includes allyl radical and allyl carbon anion. Each of the allyl species has three p orbitals, but the number of π electrons is different. There are two π electrons in allyl carbocation, three π electrons in allyl radical, and four π electrons in allyl carbon anion.

The understanding of the special stability of the allyl system species can be achieved in two ways: resonance stabilization effect theory or molecular orbital theory.

Resonance Stabilization Effect Theory for Allylic System

The stability a species gains from having charge delocalization through resonance contributors is called the resonance stabilization effect (refer to section 1.3 in Book I). All the allyl species have two equivalent resonance structures, and the actual structure is a hybrid of the two. Charges (or single electrons) can be delocalized to the other carbon as well, instead of just staying on one spot, therefore the whole allyl species has special stability.

Molecular Orbital Theory for Allyl System

Molecular orbital (MO) theory focuses on the combination of atomic orbitals to form new molecular orbitals. When atomic orbitals combine to form molecular orbitals, the number of MOs always equals the number of atomic orbitals that combine. When atomic orbitals combine with the same phase, a bonding molecular orbital is formed; and the overlap of two atomic orbitals with opposite phases results in the antibonding molecular orbital. The energy of electrons in a bonding MO is less than that in the separate atomic orbital, and the energy of electrons in an antibonding MO is greater than that in the atomic orbital. The nonbonding MO is in the same energy level as the atomic orbital. All the rules for assigning electrons to atomic orbitals also apply to molecular orbitals.

For allyl systems, we will just consider the p molecular orbitals that arise from the combination of p atomic orbitals. Since each carbon atom has one 2p orbital, there total of three 2p orbitals. The combination of them results in three π molecular orbitals, that is bonding, nonbonding, and antibonding orbitals (Fig. 3.1d). The nonbonding π MO has a node (nodal plane) at the middle carbon, and the antibonding π MO has two nodes (nodal planes) that separate the opposite phases of the lobes. The simplified sketching of the π MOs is shown in the diagram below.

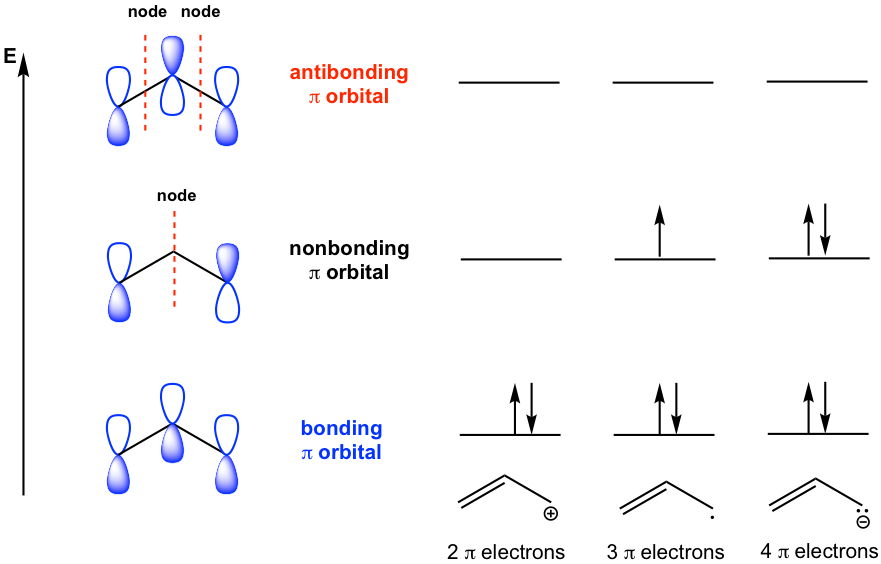
It is important to know the number of π electrons for each allyl species, which is indicated in the structure of each species. For all the allyl species, the lowest bonding π MO is always filled up with two electrons. The nonbonding MO has none, one or two electrons for different species. However, since there is no electron in the antibonding MO, the energy of each allyl system is lowered overall (and thus stabilized), regardless of cation, radical, or anion.