4.4 2D Inequality and Absolute Value Graphs
Graphing a 2D Inequality
To graph an inequality, borrow the strategy used to draw a line graph in 2D. To do this, replace the inequality with an equal sign.
Example 4.4.1
Consider the following inequalities:
\[\begin{array}{rrrrr}
3x&+&2y&<&12 \\
3x&+&2y&\le &12 \\
3x&+&2y&>&12 \\
3x&+&2y&\ge &12
\end{array}\]
All can be changed to [latex]3x + 2y = 12[/latex] by replacing the inequality sign with =.
It is then possible to create a data table using the new equation.
Create a data table of values for the equation [latex]3x + 2y = 12.[/latex]
| [latex]x[/latex] | [latex]y[/latex] |
|---|---|
| 0 | 6 |
| 2 | 3 |
| 4 | 0 |
| 6 | −3 |
Using these values, plot the data points on a graph.
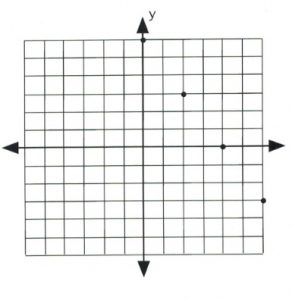
Once the data points are plotted, draw a line that connects them all. The type of line drawn depends on the original inequality that was replaced.
If the inequality had ≤ or ≥, then draw a solid line to represent data points that are on the line.
![]()
If the inequality had < or >, then draw a dashed line instead to indicate that some data points are excluded.
![]()
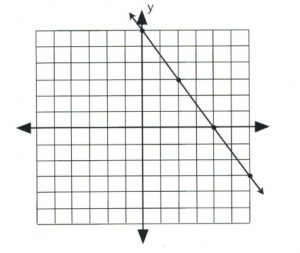
If the inequality is either [latex]3x + 2y \le 12[/latex] or [latex]3x + 2y \ge 12[/latex], then draw its graph using a solid line and solid dots.
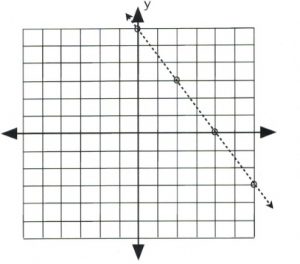
If the inequality is either [latex]3x + 2y < 12[/latex] or [latex]3x + 2y > 12[/latex], then draw its graph using a dashed line and hollow dots.
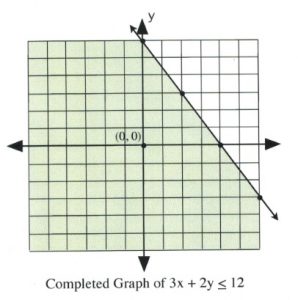
There remains only one step to complete this graph: finding which side of the line makes the inequality true and shading it. The easiest way to do this is to choose the data point [latex](0, 0)[/latex].
It is evident that, for [latex]3(0) + 2(0) \le 12[/latex] and [latex]3(0) + 2(0) < 12[/latex], the data point [latex](0, 0)[/latex] is true for the inequality. In this case, shade the side of the line that contains the data point [latex](0, 0)[/latex].
It is also clear that, for [latex]3(0) + 2(0) \ge 12[/latex] and [latex]3(0) + 2(0) > 12[/latex], the data point [latex](0, 0)[/latex] is false for the inequality. In this case, shade the side of the line that does not contain the data point [latex](0, 0)[/latex].
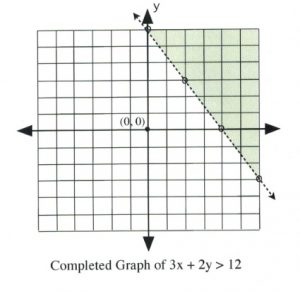 12. The side without (0, 0) is shaded." width="300" height="292">
12. The side without (0, 0) is shaded." width="300" height="292">
Graphing an Absolute Value Function
To graph an absolute value function, first create a data table using the absolute value part of the equation.
The data point that is started with is the one that makes the absolute value equal to 0 (this is the [latex]x[/latex]-value of the vertex). Calculating the value of this point is quite simple.
For example, for [latex]| x - 3 |[/latex], the value [latex]x = 3[/latex] makes the absolute value equal to 0.
Examples of others are:
\[\begin{array}{rrrrrrrrr}
|x&+&2|&=&0&\text{when}&x&=&-2 \\
|x&-&11|&=&0&\text{when}&x&=&11 \\
|x&+&9|&=&0&\text{when}&x&=&-9 \\
\end{array}\]
The graph of an absolute value equation will be a V-shape that opens upward for any positive absolute function and opens downward for any negative absolute value function.
Example 4.4.2
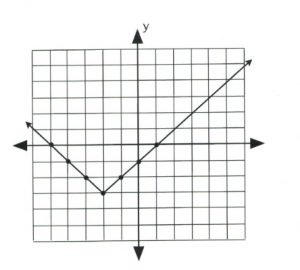
Plot the graph of [latex]y = | x + 2 | - 3.[/latex]
The data point that gives the [latex]x[/latex]-value of the vertex is [latex]| x + 2 | = 0,[/latex] in which [latex]x = -2.[/latex] This is the first value.
For [latex]x = -2, y = | -2 + 2 | - 3,[/latex] which yields [latex]y = -3.[/latex]
Now pick [latex]x[/latex]-values that are larger and less than −2 to get three data points on both sides of the vertex, [latex](-2, -3).[/latex]
| [latex]x[/latex] | [latex]y[/latex] |
|---|---|
| 1 | 0 |
| 0 | −1 |
| −1 | −2 |
| −2 | −3 |
| −3 | −2 |
| −4 | −1 |
| −5 | 0 |
Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.
Example 4.4.3
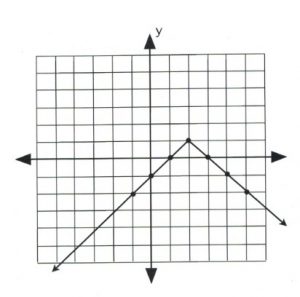
Plot the graph of [latex]y = -| x - 2 | + 1.[/latex]
The data point that gives the [latex]x[/latex]-value of the vertex is [latex]| x - 2 | = 0,[/latex] in which [latex]x = 2.[/latex] This is the first value.
For [latex]x = 2, y = -| 2 - 2 | + 1,[/latex] which yields [latex]y = 1.[/latex]
Now pick [latex]x[/latex]-values that are larger and less than 2 to get three data points on both sides of the vertex, [latex](2, 1).[/latex]
| [latex]x[/latex] | [latex]y[/latex] |
|---|---|
| 5 | −2 |
| 4 | −1 |
| 3 | 0 |
| 2 | 1 |
| 1 | 0 |
| 0 | −1 |
| −1 | −2 |
Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.
Questions
For questions 1 to 8, graph each linear inequality.
- [latex]y > 3x + 2[/latex]
- [latex]3x - 4y > 12[/latex]
- [latex]2y \ge 3x + 6[/latex]
- [latex]3x - 2y \ge 6[/latex]
- [latex]2y > 5x + 10[/latex]
- [latex]5x + 4y > -20[/latex]
- [latex]4y \ge 5x + 20[/latex]
- [latex]5x + 2y \ge -10[/latex]
For questions 9 to 16, graph each absolute value equation.
- [latex]y=|x-4|[/latex]
- [latex]y=|x-3|+3[/latex]
- [latex]y=|x-2|[/latex]
- [latex]y=|x-2|+2[/latex]
- [latex]y=-|x-2|[/latex]
- [latex]y=-|x-2|+2[/latex]
- [latex]y=-|x+2|[/latex]
- [latex]y=-|x+2|+2[/latex]

