11.8 Sine and Cosine Laws
Right angle trigonometry is generally limited to triangles that contain a right angle. It is possible to use trigonometry with non-right triangles using two laws: the sine law and the cosine law.
The Law of Sines
The sine law is a ratio of sines and opposite sides. The law takes the following form:
\[\dfrac{a}{\text{sin }A}\hspace{0.25in} =\hspace{0.25in} \dfrac{b}{\text{sin }B}\hspace{0.25in} =\hspace{0.25in} \dfrac{c}{\text{sin }C}\]
Sometimes, it is written and used as the reciprocal of the above:
\[\dfrac{\text{sin }A}{a}\hspace{0.25in} =\hspace{0.25in} \dfrac{\text{sin }B}{b}\hspace{0.25in} =\hspace{0.25in} \dfrac{\text{sin }C}{c}\]
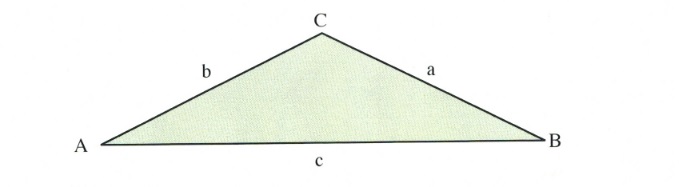
The law of sine is used when either two sides and one opposite angle of one of the sides are known, or when there are two angles and one side of one of the angles. If there are two given angles of a triangle, then all three angles are known, since [latex]A^{\circ} + B^{\circ} + C^{\circ} = 180^{\circ}.[/latex]
The sine law is a very useful law with one caveat in that it is possible to sometimes have two triangles (one larger and one smaller) that generate the same result. This is termed the ambiguous case and is described later in this section.
There are also textbook errors where the data given for the triangle is impossible to create. For instance:
Example 11.8.1
Can the following triangle exist?
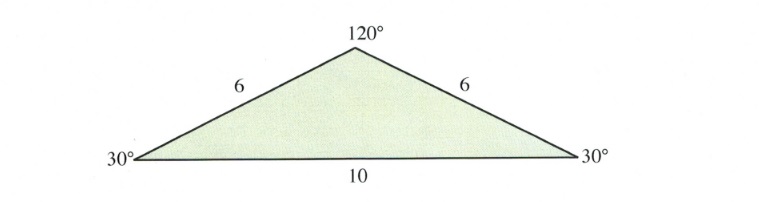
If this triangle can exist, then the ratio of sines for the angles to the opposite sides should equate.
\[\dfrac{6}{\text{sin }30^{\circ}}\hspace{0.25in} = \hspace{0.25in} \dfrac{6}{\text{sin }30^{\circ}}\hspace{0.25in} = \hspace{0.25in} \dfrac{10}{\text{sin }120^{\circ}}\]
Reducing this yields:
\[\dfrac{6}{0.5} \hspace{0.25in} = \hspace{0.25in}\dfrac{6}{0.5} \hspace{0.25in} = \hspace{0.25in} \dfrac{10}{0.866}\]
In checking this out, we find that 12 = 12 ≠ 11.55.
This means that this triangle cannot exist.
Example 11.8.2
Find the correct length of the side opposite 120° in the triangle shown below.
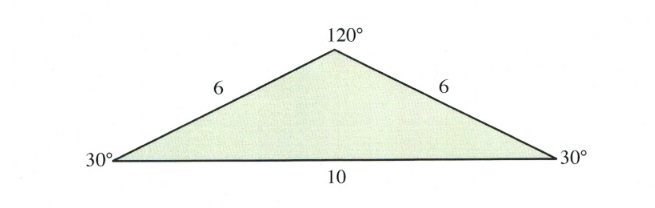
For this triangle, the ratio to solve is:
\[\dfrac{6}{\text{sin }30^{\circ}}\hspace{0.25in}=\hspace{0.25in}\dfrac{6}{\text{sin }30^{\circ}} \hspace{0.25in}=\hspace{0.25in}\dfrac{x}{\text{sin }120^{\circ}} \]
We only need to use one portion of this, so:
\[\dfrac{6}{\text{sin }30^{\circ}}\hspace{0.25in}=\hspace{0.25in}\dfrac{x}{\text{sin }120^{\circ}}\]
Multiplying both sides of this by sin 120°, we are left with:
\[x=\dfrac{6\text{ sin }120^{\circ}}{\text{sin }30^{\circ}}\]
This leaves us with [latex]x = 10.29[/latex].
Example 11.8.3
Find the correct length of the side opposite 120° in the triangle shown below.
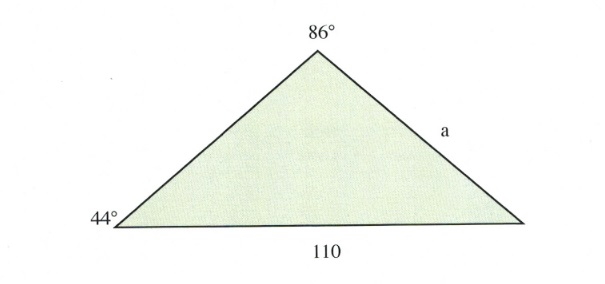
For this triangle, the ratio to solve is:
\[\dfrac{a}{\text{sin }44^{\circ}}\hspace{0.25in}=\hspace{0.25in}\dfrac{110}{\text{sin }86^{\circ}}\]
Multiplying both sides by sin 44° leaves us with:
\[a=\dfrac{110\text{ sin }44^{\circ}}{\text{sin }86^{\circ}}\]
Example 11.8.4
Find the unknown angle shown in the triangle shown below.
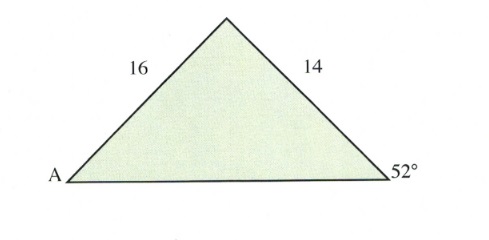
For this triangle, the ratio to solve is:
\[\dfrac{14}{\text{sin }A}\hspace{0.25in}=\hspace{0.25in}\dfrac{16}{\text{sin }52^{\circ}}\]
Isolating sin A yields:
\[\text{sin }A=\dfrac{14\text{ sin }52^{\circ}}{16}\]
We now need to take the inverse sin of both sides to solve for A:
\[\begin{array}{l}
A=\text{sin}^{-1}\left(\dfrac{14\text{ sin }52^{\circ}}{16}\right) \\ \\
A=43.6^{\circ}
\end{array}\]
The Ambiguous Case
It is possible, when given the right data, to create two different triangles.
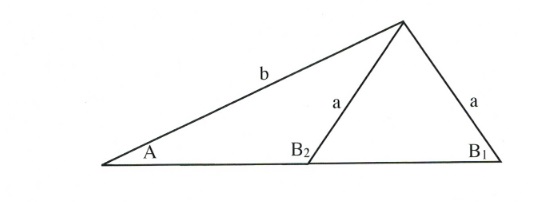
You can see from the triangle shown above that it is possible to have two angles, B1 and B2, for side [latex]b[/latex]. Using the sine law, you will always end up solving for B1, the angle for the largest triangle. If you are trying to solve for the smaller triangle, then you only need to subtract B1 from 180°.
For example, if B1 = 50°, then B2 = 180° − B1. This means B2 = 180° − 50° or 130°.
If the angle you solve for when using the sine law is smaller than it should be, then correct for it as we just did above.
The Law of Cosines
The Law of Cosines is the generalized law of the Pythagorean Theorem [latex](a^2 + b^2 = c^2).[/latex]
The Law of Cosines is generally written in three different forms, which are as follows:
\[\begin{array}{l}
a^2 = b^2 + c^2 – 2bc\text{ cos }A \\
b^2 = a^2 + c^2 – 2ac\text{ cos }B \\
c^2 = a^2 + b^2 – 2ab\text{ cos }C
\end{array}\]
All forms revert back to one of the three regular forms of the Pythagorean theorem [latex](a^2 = b^2 + c^2, b^2 = a^2 + c^2, c^2 = a^2 + b^2)[/latex] if [latex]A, B[/latex] or [latex]C[/latex] is 90°, since [latex]\text{cos }90^{\circ} = 0.[/latex] The following examples illustrate the usage of the cosine law in trigonometry
Example 11.8.5
Find the unknown angle shown in the triangle shown below.
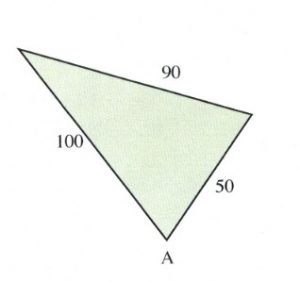
For this triangle:
\[\begin{array}{l}
A=\text{find} \\ \\
a=90 \\ \\
b=50 \\ \\
c=100
\end{array}\]
Note that [latex]b[/latex] and [latex]c[/latex] could be switched around. Now, to solve:
[latex]\begin{array}{rrlllll} a^2 &= &\phantom{-}b^2 &+ &c^2 &-& 2bc\text{ cos }A \\ \\ 90^2 &= &\phantom{-}50^2 &+ &100^2 &- &2(50)(100)\text{ cos } A \\ 8100& =&\phantom{-}2500 &+ &10000& - &10000\text{ cos }A \\ -2500&&-2500&-&10000&& \\ \hline -4400& =&-10000&\text{ cos }&A&& \\ \\ \text{ cos }A& =&\dfrac{-4400}{-10000}&&&& \\ \\ B& =&\text{cos}^{-1}0.44&&&& \\ \\ B&=&63.9^{\circ}&&&& \end{array}[/latex]
Example 11.8.6
Find the unknown side shown in the triangle shown below.
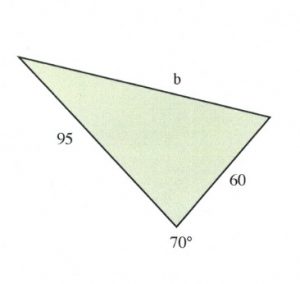For this triangle:
\[\begin{array}{l}
B=70^{\circ} \\ \\
a=95 \\ \\
b=\text{find} \\ \\
c=60
\end{array}\]
Note that [latex]b[/latex] and [latex]c[/latex] could be switched around. Now, to solve:
\[\begin{array}{l}
b^2=a^2+c^2-2ac\text{ cos }B \\ \\
b^2=95^2+60^2-2(95)(60)\text{ cos }70^{\circ} \\
b^2=9025+3600-11400(0.34202) \\
b^2=12625 – 3899 \\
b^2=8726 \\ \\
b=\sqrt{8726} \\
b=93.4
\end{array}\]
Unlike with the law of sines, there should be no ambiguous cases with the law of cosines.
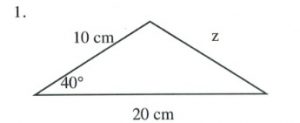
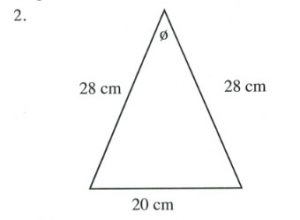
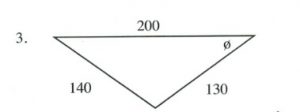
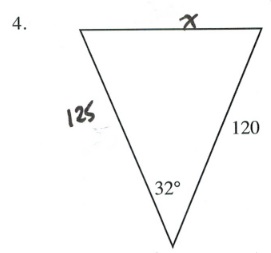
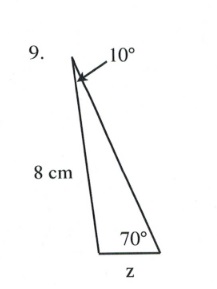
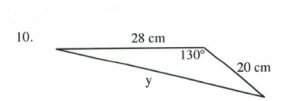
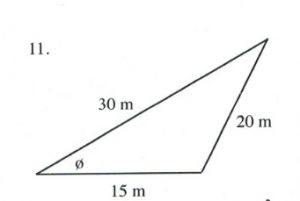
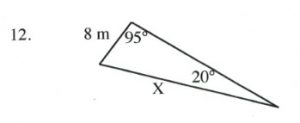
Questions
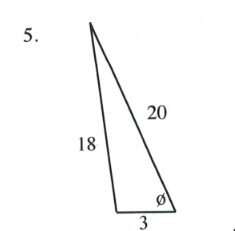
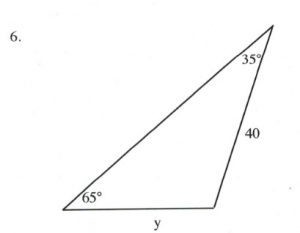
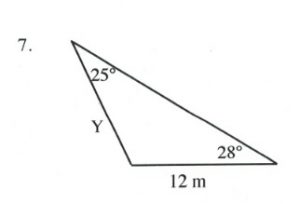
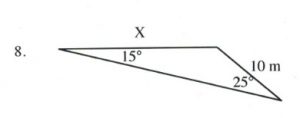
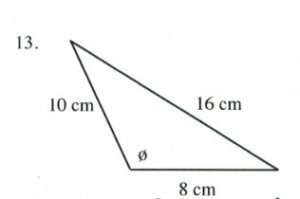
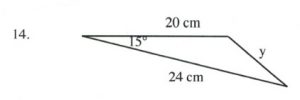
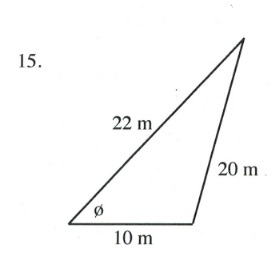
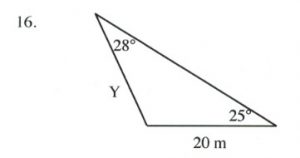
Solve all unknowns in the following non-right triangles using either the law of sines or cosines.
