Midterm 2: Version A Answer Key
-
[latex]x+2y=-5[/latex] [latex]x[/latex] [latex]y[/latex] 0 [latex]-\dfrac{5}{2}[/latex] −5 0 [latex]x-y=-2[/latex] [latex]x[/latex] [latex]y[/latex] 0 2 −2 0 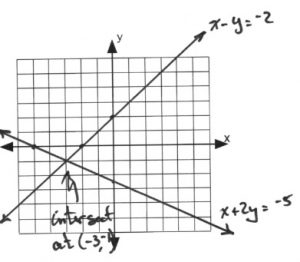
- [latex]\begin{array}{ll} \\ \\ \\ \\ \\ \\ \\ \\ \begin{array}{rrrrrl} &(4x&-&3y&=&13)(2) \\ &(5x&-&2y&=&\phantom{1}4)(-3) \\ \\ &8x&-&6y&=&\phantom{-}26 \\ +&-15x&+&6y&=&-12 \\ \hline &&&-7x&=&\phantom{-}14 \\ \\ &&&x&=&\dfrac{14}{-7}\text{ or }-2 \end{array} & \hspace{0.25in} \begin{array}{rrcrl} \\ 5x&-&2y&=&\phantom{+1}4 \\ 5(-2)&-&2y&=&\phantom{+1}4 \\ -10&-&2y&=&\phantom{+1}4 \\ +10&&&&+10 \\ \hline &&-2y&=&\phantom{+}14 \\ \\ &&y&=&\dfrac{14}{-2}\text{ or }-7 \end{array} \end{array}[/latex]
[latex](-2,-7)[/latex] - [latex]\begin{array}{rrrrrl} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ &x&-&2y&=&-5 \\ &(2x&+&y&=&\phantom{-}5)(2) \\ \\ &x&-&2y&=&-5 \\ +&4x&+&2y&=&10 \\ \hline &&&5x&=&5 \\ &&&x&=&1 \\ \\ \therefore &2(1)&+&y&=&\phantom{-}5 \\ &-2&&&&-2 \\ \hline &&&y&=&\phantom{-}3 \end{array}[/latex]
- [latex]\begin{array}{ll} \\ \\ \\ \\ \\ \\ \\ \begin{array}{rrrrrrrl} \\ \\ \\ \\ \\ \\ &(x&+&y&+&2z&=&0)(-2) \\ \\ &-2x&-&2y&-&4z&=&0 \\ +&2x&&&+&z&=&1 \\ \hline &&&-2y&-&3z&=&1 \\ \\ &&&(-2y&-&3z&=&1)(3) \\ &&&(3y&+&4z&=&0)(2) \\ \\ &&&-6y&-&9z&=&3 \\ &&+&6y&+&8z&=&0 \\ \hline &&&&&-z&=&3 \\ &&&&&z&=&-3 \\ \end{array} & \hspace{0.25in} \begin{array}{rrcrl} \\ \\ 3y&+&4z&=&0 \\ 3y&+&4(-3)&=&0 \\ 3y&-&12&=&0 \\ &&3y&=&12 \\ &&y&=&4 \\ \\ 2x&+&z&=&1 \\ 2x&+&(-3)&=&1 \\ &&2x&=&4 \\ &&x&=&2 \\ \end{array} \end{array}[/latex]
[latex](2,4,-3)[/latex] - [latex]28-\{5x-\cancel{\left[6x-3(5-2x)\right]^0}1\}+5x^2[/latex]
[latex]28-\{5x-1\}+5x^2[/latex]
[latex]28-5x+1+5x^2[/latex]
[latex]5x^2-5x+29[/latex] - [latex]\begin{array}{rrrcrl} \\ \\ \\ \\ \\ \\ \\ \\ \\ &a&-&3&& \\ \times &a&-&3&& \\ \hline &a^2&-&3a&& \\ +&&-&3a&+&9 \\ \hline &a^2&-&6a&+&9 \\ \\ &a^2&-&6a&+&9 \\ \times&&&&&4a^2 \\ \hline &4a^4&-&24a^3&+&36a^2 \\ \end{array}[/latex]
- [latex]\begin{array}{rrrrrlrrrr} \\ \\ \\ \\ \\ \\ &x^2&+&2x&+&3&&&& \\ \times&x^2&+&2x&+&3&&&& \\ \hline &x^4&+&2x^3&+&3x^2&&&& \\ &&&2x^3&+&4x^2&+&6x&& \\ +&&&&&3x^2&+&6x&+&9 \\ \hline &x^4&+&4x^3&+&10x^2&+&12x&+&9 \end{array}[/latex]
- [latex]\polylongdiv{2x^3-7x^2+15}{x-2}[/latex]
- [latex]a(2b+3c)-2(2b+3c)[/latex]
[latex](2b+3c)(a-2)[/latex] - [latex]a^2-5ab+3ab-15b^2[/latex]
[latex]a(a-5b)+3b(a-5b)[/latex]
[latex](a-5b)(a+3b)[/latex] - [latex]x^2(x+1)-9(x+1)[/latex]
[latex](x^2-9)(x+1)[/latex]
[latex](x+3)(x-3)(x+1)[/latex] - [latex](x)^3-(4y)^3[/latex]
[latex](x-4y)(x^2+4xy+16y^2)[/latex] - [latex]\phantom{1}[/latex]
[latex]B+S=35\Rightarrow B=35-S \\[/latex]
[latex]\begin{array}{ll} \begin{array}{rrrrrrrr} &B&-&10&=&2(S&-&10) \\ &35-S&-&10&=&2S&-&20 \\ &25&-&S&=&2S&-&20 \\ +&20&+&S&&S&+&20 \\ \hline &&&45&=&3S&& \end{array} & \hspace{0.25in} \begin{array}{rrl} S&=&\dfrac{45}{3}\text{ or }15 \\ \\ \therefore B&=&35-S \\ B&=&35-15 \\ B&=&20 \\ \end{array} \end{array}[/latex] - [latex]\phantom{1}[/latex]
[latex]D+Q=20\Rightarrow Q=20-D \\[/latex]
[latex]\begin{array}{ll} \begin{array}{rrlrr} 10D&+&25Q&=&275 \\ 10D&+&25(20-D)&=&275 \\ 10D&+&500-25D&=&275 \\ &-&500&&-500 \\ \hline &&\phantom{500}-15D&=&-225 \end{array} & \hspace{0.25in} \begin{array}{rrl} D&=&\dfrac{-225}{-15}\text{ or }15 \\ \\ \therefore Q&=&20-D \\ Q&=&20-15 \\ Q&=&5 \\ \end{array} \end{array}[/latex] - [latex]\phantom{1}[/latex]
[latex]A+B=50\Rightarrow A=50-B \\[/latex]
[latex]\begin{array}{rrrrrrl} (3.95A&+&3.70(50&-&A)&=&191.25)(100) \\ \\ 395A&+&370(50&-&A)&=&19125 \\ 395A&+&18500&-&370A&=&19125 \\ &-&18500&&&&-18500 \\ \hline &&&&25A&=&625 \\ \\ &&&&A&=&\dfrac{625}{25}\text{ or 25 kg} \\ \\ &&&&B&=&50-25 \\ &&&&B&=&25 \text{ kg} \\ \end{array}[/latex]

