Answer Key 4.2

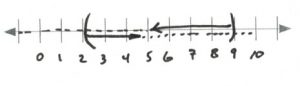
  1. [latex]\begin{array}{rrrrrrrr} \\ \\ (3)&(\dfrac{n}{3}&<&3)&\text{or}&\dfrac{-5n}{-5}&<&\dfrac{-10}{-5} \\ \\ &n&<&9&\text{or}&n&>&2 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, \infty)[/latex]  Number line with positive infinity and negative inifinty
  2. [latex]\begin{array}{rrrrrrrrr} \\ \\ \dfrac{6m}{6}&\ge & \dfrac{-24}{6}& \text{or}&m&-&7&<&-12 \\ &&&&&+&7&<&+7 \\ \hline m&\ge & -4& \text{or}&&&m&<&-5 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -5) \cup [-4, \infty)[/latex]  Numberline with (-5, infinity), (-4, infinity)
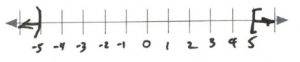
  3. [latex]\begin{array}{rrrrrrrrr} \\ \\ x&+&7& \ge& 12& \text{or}& \dfrac{9x}{9}&<&\dfrac{-45}{9} \\ &-&7&&-7&&&& \\ \hline &&x& \ge&5& \text{or}&x&<&-5 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -5) \cup [5, \infty)[/latex] Numberline (-5, infinity) ((5, positive infinity)
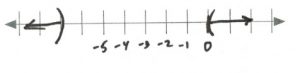
  4. [latex]\begin{array}{rrrrrrrrr} \\ \\ \dfrac{10r}{10}&>&\dfrac{0}{10}&\text{or}&r&-&5&<&-12 \\ &&&&&+&5&&+5 \\ \hline r&>&0&\text{or}&&&r&<&-7 \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -7) \cup (0, \infty)[/latex]  Number line with (- infinity, -7), (0, positive infinity)
  5. [latex]\begin{array}{rrrrrrrrr} \\ \\ x&-&6&<&-13&\text{or}&\dfrac{6x}{6}&<&\dfrac{-60}{6} \\ &+&6&&+6&&&& \\ \hline &&x&<&-7&&x&<&-10 \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -7)[/latex] Numberline (- 7, - infinity)
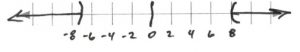
  6. [latex]\begin{array}{rrrrrrrrr} \\ \\ 9&+&n&<&2&\text{or}&\dfrac{5n}{5}&>&\dfrac{40}{5} \\ -9&&&&-9&&&& \\ \hline &&n&<&-7&\text{or}&n&>&8 \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -7)\cup (8, \infty)[/latex] Numberline (- infinity, -7) or (8, positive infinity)
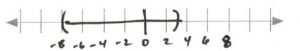
  7. [latex]\begin{array}{rrrrcrrrrr} \\ \\ (8)&(\dfrac{v}{8}&>&-1)&\text{and}&v&-&2&<&1 \\ &&&&&&+&2&&+2 \\ \hline &v&>&-8&\text{and}&&&v&<&3 \\ \\ &&-8&<&v&<&3&&& \end{array}[/latex][latex]\text{Interval notation: } [latex](-8, 3)[/latex] Numberline (-8,3)
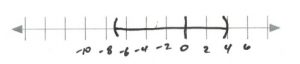
  8. [latex]\begin{array}{rrrcrrrr} \\ \\ \\ \dfrac{-9x}{-9}&<&\dfrac{63}{-9}&\text{and}&(\dfrac{x}{4}&<&1)&(4) \\ \\ x&>&-7&\text{and}&x&<&4& \\ \\ &-7&<&x&<&4&& \end{array}[/latex][latex]\text{Interval notation: } (-7, 4)[/latex]  Numberline (-7,4)
  9. [latex]\begin{array}{rrrrrrrrr} \\ \\ -8&+&b&<&-3&\text{and}&\dfrac{4b}{4}&<&\dfrac{20}{4} \\ +8&&&&+8&&&& \\ \hline &&b&<&5&&b&<&5 \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 5)[/latex] Numberline (- infinity, 5)
  10. [latex]\begin{array}{rrrcrrrr} \\ \\ \\ \\ \dfrac{-6n}{-6}&<&\dfrac{12}{-6}&\text{and}&(\dfrac{n}{3}&<&2)&(3) \\ \\ n&>&-2&\text{and}&n&<&6& \\ \\ &-2&<&n&<&6&& \end{array}[/latex][latex]\text{Interval notation: } (-2, 6)[/latex] Numberline (-2, 6)
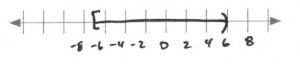
  11. [latex]\begin{array}{rrrrrcrrr} \\ \\ \\ a&+&10&\ge &3&\text{and}&\dfrac{8a}{8}&<&\dfrac{48}{8} \\ &-&10&&-10&&&& \\ \hline &&a&\ge &-7&\text{and}&a&<&6 \\ \\ &&&-7&\le &a&<&6& \end{array}[/latex][latex]\text{Interval notation: } [-7, 6)[/latex] Numberline (-7,6)
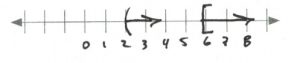
  12. [latex]\begin{array}{rrrrrcrrr} \\ \\ -6&+&v&\ge &0&\text{and}&\dfrac{2v}{2}&>&\dfrac{4}{2} \\ +6&&&&+6&&&& \\ \hline &&v&\ge &6&\text{and}&v&>&2 \end{array}[/latex][latex]\text{Interval notation: } [6, \infty)[/latex] Numberline [6, positive infinity)
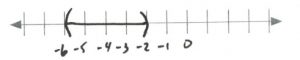
  13. [latex]\begin{array}{rrrcrrr} \\ \\ 3&<&9&+&x&<&7 \\ -9&&-9&&&&-9 \\ \hline -6&<&&x&&<&-2 \\ \end{array}[/latex][latex]\text{Interval notation: } (-6, -2)[/latex] Numberline (-6,-2)
  14. [latex]\begin{array}{rrrrrr} \\ \\ (0&\ge & \dfrac{x}{9} & \ge & -1)&(9) \\ \\ 0&\ge & x& \ge & -9& \\ \\ \end{array}[/latex][latex]\text{Interval notation: } [-9, 0][/latex] Numberline [-9,0]
  15. [latex]\begin{array}{rrrcrrr} \\ \\ \\ 11&<&8&+&k&<&12 \\ -8&&-8&&&&-8 \\ \hline 3&<&&k&&<&4 \\ \\ \end{array}[/latex][latex]\text{Interval notation: } (3, 4)[/latex] Numberline (3,4)
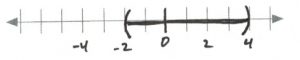
  16. [latex]\begin{array}{rrrcrrr} \\ \\ \\ -11&<&n&-&9&<&-5 \\ +9&&&+&9&&+9 \\ \hline -2&<&&n&&<&4 \\ \\ \end{array}[/latex][latex]\text{Interval notation: } (-2, 4)[/latex] Numberline (-2,4)
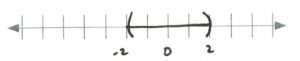
  17. [latex]\begin{array}{rrrcrrr} \\ \\ \\ -3&<&x&-&1&<&1 \\ +1&&&+&1&&+1 \\ \hline -2&<&&x&&<&2 \\ \\ \end{array}[/latex][latex]\text{Interval notation: } (-2, 2)[/latex] Numberline (-2,2)
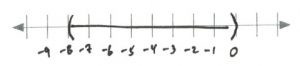
  18. [latex]\begin{array}{rrrrrr} \\ \\ \\ (-1&< & \dfrac{p}{8} & <& 0)&(8) \\ \\ -8&< & p& < & 0& \\ \\ \end{array}[/latex][latex]\text{Interval notation: } (-8, 0)[/latex] Numberline (-8,0)
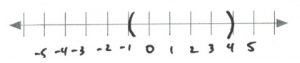
  19. [latex]\begin{array}{rrrcrrr} \\ \\ \\ \\ \\ -4&<&8&-&3m&<&11 \\ -8&&-8&&&&-8 \\ \hline \dfrac{-12}{-3}&<&&\dfrac{-3m}{-3}&&<&\dfrac{3}{-3} \\ \\ 4&>&&m&&>&-1 \end{array}[/latex][latex]\text{Interval notation: } (-1, 4)[/latex]  Numberline (-1,4)
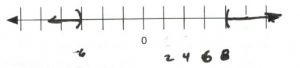
  20. [latex]\begin{array}{rrrrrcrrrrr} \\ \\ \\ \\ \\ 3&+&7r&>&59&\text{or} &-6r&-&3&>&33 \\ -3&&&&-3&&&+&3&>&+3 \\ \hline &&\dfrac{7r}{7}&>&\dfrac{56}{7}&\text{or} &&&\dfrac{-6r}{-6}&>&\dfrac{36}{-6} \\ \\ &&r&>&8&\text{or} &&&r&<&-6 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -6) \cup (8, \infty)[/latex] Numberline (- infinity, -6) or (6, inifinity)
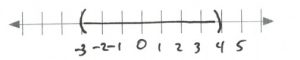
  21. [latex]\begin{array}{rrrcrrr} \\ \\ \\ \\ \\ -16&<&2n&-&10&<&-2 \\ +10&&&+&10&&+10 \\ \hline \dfrac{-6}{2}&<&&\dfrac{2n}{2}&&<&\dfrac{8}{2} \\ \\ -3&<&&n&&<&4 \end{array}[/latex][latex]\text{Interval notation: } (-3, 4)[/latex] Numberline (-3,4)
  22. [latex]\begin{array}{rrrrrcrrrrr} \\ \\ \\ \\ \\ -6&-&8x&\ge &-6&\text{or} &2&+&10x&>&82 \\ +6&&&&+6&&-2&&&>&-2 \\ \hline &&\dfrac{-8x}{-8}&\ge&\dfrac{0}{-8}&&&&\dfrac{10x}{10}&>&\dfrac{80}{10} \\ \\ &&x&\le &0&&\text{or}&&x&>&8 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 0] \cup (8, \infty)[/latex] Numberline (- infinity,0) or (8, infinity)
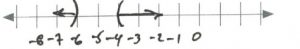
  23. [latex]\begin{array}{rrrrrcrrrrr} \\ \\ \\ \\ \\ -5b&+&10&<&30&\text{and} &7b&+&2&<&-40 \\ &&-10&&-10&&&-&2&&-2 \\ \hline &&\dfrac{-5b}{-5}&<&\dfrac{20}{-5}&&&&\dfrac{7b}{7}&<&\dfrac{-42}{7} \\ \\ &&b&>&-4&&\text{and}&&b&<&-6 \end{array}[/latex]∴ [latex]\text{No solution}[/latex] No solution
  24. [latex]\begin{array}{rrrrrcrrrrr} \\ \\ \\ \\ \\ n&+&10&\ge &15&\text{or} &4n&-&5&<&-1 \\ &-&10&&-10&&&+&5&&+5 \\ \hline &&n&\ge&5&&&&\dfrac{4n}{4}&<&\dfrac{4}{4} \\ \\ &&n&\ge &5&&\text{or}&&n&<&1 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 1) \cup [5, \infty)[/latex]  Numberline (negative infinity, 1) or (5 positive inifinity)
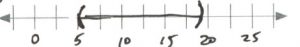
  25. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ 3x&-&9&<&2x&+&10&\text{and}&5&+&7x&<&10x&-&10 \\ -2x&+&9&&-2x&+&9&&-5&-&10x&&-10x&-&5 \\ \hline &&x&<&19&&&&&&\dfrac{-3x}{-3}&<&\dfrac{-15}{-3}&& \\ \\ &&x&<&19&&&\text{and}&&&x&>&5&& \\ \\ &&&&&5&<&x&<&19&&&&& \end{array}[/latex][latex]\text{Interval notation: } (5, 19)[/latex] Numberline(5,19)
  26. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ 4n&+&8&<&3n&-&6&\text{or}&10n&-&8&\ge &9&+&9n \\ -3n&-&8&&-3n&-&8&&-9n&+&8&&+8&-&9n \\ \hline &&n&<&-14&&&\text{or}&&&n&\ge &17&& \\ \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -14) \cup [17, \infty)[/latex] Numerline (- infinity, -14), or (16, positive infinity)
  27. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ -8&-&6v&<&8&-&8v&\text{and}&7v&+&9&<&6&+&10v \\ +8&+&8v&&+8&+&8v&&-10v&-&9&&-9&-&10v \\ \hline &&\dfrac{2v}{2}&<&\dfrac{16}{2}&&&&&&\dfrac{-3v}{-3}&<&\dfrac{-3}{-3}&& \\ \\ &&v&<&8&&&\text{and}&&&v&>&1&& \\ \\ &&&&&1&<&v&<&8&&&&& \end{array}[/latex][latex]\text{Interval notation: } (1, 8)[/latex] Numberline (1,8)
  28. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ 5&-&2a&\ge &2a&+&1&\text{or}&10a&-&10&\ge &9a&+&9 \\ -5&-&2a&&-2a&-&5&&-9a&+&10&&-9a&+&10 \\ \hline &&\dfrac{-4a}{-4}&\ge &\dfrac{-4}{-4}&&&&&&a&\ge&19&& \\ \\ &&a&\le &1&&&\text{or}&&&a&\ge &19&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 1] \cup [19, \infty)[/latex] Numberline (- infinity, 1) or (19, positive infinity)
  29. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ 1&+&5k&\ge &7k&-&3&\text{or}&k&-&10&>&2k&+&10 \\ -1&-&7k&&-7k&-&1&&-2k&+&10&&-2k&+&10 \\ \hline &&\dfrac{-2k}{-2}&\ge &\dfrac{-4}{-2}&&&&&&-k&>&20&& \\ \\ &&k&\le &2&&&\text{or}&&&k&<&-20&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 2][/latex] Numberline (-2, negative infinity]
  30. [latex]\begin{array}{rrrrrrrcrrrrrrl} \\ \\ \\ 8&-&10r&<&8&+&4r&\text{or}&-6&+&8r&<&2&+&8r \\ -8&-&4r&&-8&-&4r&&+6&-&8r&&+6&-&8r \\ \hline &&\dfrac{-14r}{-14}&<&\dfrac{0}{-14}&&&&&&0&<&8&\leftarrow &\text{This is always true} \\ \\ &&r&>&0&&&\text{or}&&&r&\in &\mathbb{R} && \end{array}[/latex][latex]\text{Interval notation: } (-\infty, \infty)[/latex] Numberline (negative infinity, positive infinity)
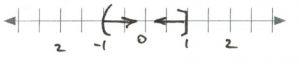
  31. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ 2x&+&9&\ge &10x&+&1&\text{and}&3x&-&2&<&7x&+&2 \\ -10x&-&9&&-10x&-&9&&-7x&+&2&&-7x&+&2 \\ \hline &&\dfrac{-8x}{-8}&\ge &\dfrac{-8}{-8}&&&&&&\dfrac{-4x}{-4}&<&\dfrac{4}{-4}&& \\ \\ &&x&\le &1&&&\text{and}&&&x&>&-1&& \\ \\ &&&&&-1&<&x&\le &1&&&&& \end{array}[/latex][latex]\text{Interval notation: } (-1, 1][/latex] Numberlin (-1,1)
  32. [latex]\begin{array}{rrrrrrrcrrrrrrr} \\ \\ \\ \\ \\ -9m&+&2&< &-10&-&6m&\text{or}&-m&+&5&\ge &10&+&4m \\ +6m&-&2&&-2&+&6m&&-4m&-&5&&-5&-&4m \\ \hline &&\dfrac{-3m}{-3}&<&\dfrac{-12}{-3}&&&&&&\dfrac{-5m}{-5}&\ge &\dfrac{5}{-5}&& \\ \\ &&m&>&4&&&\text{or}&&&m&\le &-1&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -1] \cup (4, \infty)[/latex] Numberline (- infinity, -1) or (4, infinity)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate Algebra (Convert to MathJax) Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book