Answer Key 4.1

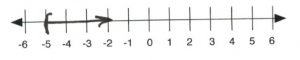
  1. [latex](-5, \infty)[/latex]     -5, infinity
  2. [latex](4, \infty)[/latex]       4, inifinity
  3. [latex](-2, \infty)[/latex]   -2, inifinity
  4. [latex](-\infty, 1][/latex]     - infinity, 1
  5. [latex](-\infty, 5][/latex]    - infinity, 5
  6. [latex](-5, \infty)[/latex]     -5, inifinity
  7. [latex]x>-5\hspace{0.25in} (-5, \infty)[/latex]     image -5, -5, inifinity” width=”367″ height=”71″>
  8. [latex]x>0\hspace{0.25in} (0, \infty)[/latex]        image 0), 0, inifinity ” width=”382″ height=”65″>
  9. [latex]x\ge -3 \hspace{0.25in} [-3, \infty)[/latex]     image or equal to -3, (-3, inifinity)” width=”388″ height=”57″>
  10. [latex]x\le 6 \hspace{0.25in} (-\infty, 6][/latex]     x < 6, - infinity, 6
  11. [latex]x\le -1 \hspace{0.25in} (-\infty, -1][/latex]     x < or equal to -1, (-1, - inifinity)
  12. [latex]x < 6 \hspace{0.25in} (-\infty, 6)[/latex]      x < 6 , (-infinity, 6)
  13. [latex]\begin{array}{rrrl} \\ \\ (\dfrac{x}{11}&\ge &10)&(11) \\ \\ x& \ge & 110 & \end{array}[/latex][latex]\text{Interval notation: } [110,\infty)[/latex]  Number line
  14. [latex]\begin{array}{rrrl} \\ \\ (-2 &\le & \dfrac{n}{13})&(13) \\ \\ -26& \le & n & \end{array}[/latex][latex]\text{Interval notation: } [-26, \infty)[/latex] Number line
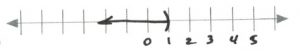
  15. [latex]\begin{array}{rrrlr} \\ \\ 2 &+ & r&<&3 \\ -2&&&& -2 \\ \hline &&r&<&1 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 1)[/latex] Number line
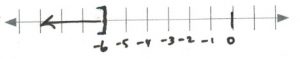
  16. [latex]\begin{array}{rrrl} \\ \\ (\dfrac{m}{5} &\le & -\dfrac{6}{5})&(5) \\ \\ m& \le & -6 & \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -6][/latex] Number line
  17. [latex]\begin{array}{rrrrrr} \\ \\ \\ \\ \\ 8&+&\dfrac{n}{3}&\ge & 6 & \\ -8&&&&-8 & \\ \hline &&(\dfrac{n}{3} &\ge & -2)& (3) \\ \\ &&n & \ge & -6 & \end{array}[/latex][latex]\text{Interval notation: } [-6, \infty)[/latex] Number line
  18. [latex]\begin{array}{rrrrr} \\ \\ \\ \\ \\ 11&>&8&+ & \dfrac{x}{2} \\ -8&&-8&& \\ \hline (3 &> & \dfrac{x}{2})& (2)& \\ \\ 6 & > & x && \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 6)[/latex] Number line
  19. [latex]\left(2>\dfrac{(a-2)}{5}\right)(5)[/latex][latex]\begin{array}{rrrrr} 10&>&a&-&2 \\ +2&&&+&2 \\ \hline 12&>&a&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 12)[/latex] Number line
  20. [latex]\left(\dfrac{(v-9)}{-4}\le 2 \right)(-4)[/latex][latex]\begin{array}{rrrrr} v&-&9&\ge &-8 \\ &+&9&&+9 \\ \hline &&v&\ge &1 \end{array}[/latex][latex]\text{Interval notation: } [1, \infty)[/latex]  Number line
  21. [latex]\begin{array}{rrrrl} \\ \\ \\ \\ \\ -47&\ge &8&-& 5x \\ -8&&-8&& \\ \hline \dfrac{-55}{-5}&\ge &\dfrac{-5x}{-5} && \\ \\ 11& \le & x && \end{array}[/latex][latex]\text{Interval notation: } [11, \infty)[/latex]  Number line
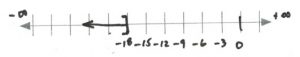
  22. [latex]\left(\dfrac{(6+x)}{12}\le -1 \right)(12)[/latex][latex]\begin{array}{rrrrr} 6&+&x&\le &-12 \\ -6&&&&-6 \\ \hline &&x&\le &-18 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -18][/latex] Number line
  23. [latex]\begin{array}{rrrrl} \\ \\ \\ \\ \\ \dfrac{-2}{-2}(3&+ &k)&<& \dfrac{-44}{-2} \\ \\ 3&+ &k &>&22 \\ -3&&&&-3 \\ \hline && k&>&19 \end{array}[/latex][latex]\text{Interval notation: } (19, \infty)[/latex] Number line
  24. [latex]\begin{array}{rrrrr} \\ \\ \\ \\ \\ -7n&- &10&\ge &60 \\ &+&10&&+10 \\ \hline &&\dfrac{-7n}{-7}&\ge & \dfrac{70}{-7} \\ \\ &&n&\le &-10 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -10][/latex] Number line
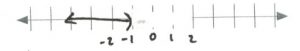
  25. [latex]\begin{array}{rrrrl} \\ \\ \\ \\ \\ \dfrac{18}{-2}&<&\dfrac{-2}{-2}(-8&+&p) \\ \\ -9&>&-8&+&p \\ +8&&+8&& \\ \hline -1&>&p&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -1)[/latex]  Number line
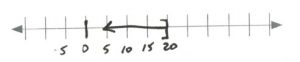
  26. [latex]\left(5> \dfrac{x}{5}+1 \right)(5)[/latex][latex]\begin{array}{rrrrr} 25&\ge &x&+ &5 \\ -5&&&&-5 \\ \hline 20&\ge &x& & \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 20][/latex]  Number line
  27. [latex]\begin{array}{rrrrr} \\ \\ \\ \\ \\ \dfrac{24}{-6}&\ge &\dfrac{-6}{-6}(m&-&6) \\ \\ -4&\le &m&-&6 \\ +6&&&+&6 \\ \hline 2&\le &m&& \end{array}[/latex][latex]\text{Interval notation: } [2, \infty)[/latex] 
  28. [latex]\begin{array}{rrrrr} \\ \\ \\ \\ \\ \dfrac{-8}{-8}(n&-&5)&\ge &\dfrac{0}{-8} \\ \\ n&-&5&\le &0 \\ &+&5&&+5 \\ \hline &&n&\le &5 \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 5][/latex] 
  29. [latex]\begin{array}{rrrrrrl} \\ \\ \\ \\ \\ \\ -r&-&5(r&-&6)&<&-18 \\ -r&-&5r&+&30&<&-18 \\ &&&-&30&&-30 \\ \hline &&&&\dfrac{-6r}{-6}&<&\dfrac{-48}{-6} \\ \\ &&&&r&>&8 \\ \end{array}[/latex][latex]\text{Interval notation: } (8, \infty)[/latex] 
  30. [latex]\begin{array}{rrlrr} \\ \\ \\ \\ \\ \\ \dfrac{-60}{-4}&\ge &\dfrac{-4}{-4}(-6x&-&3) \\ \\ 15&\le &-6x&-&3 \\ +3&&&+&3 \\ \hline \dfrac{18}{-6}&\le&\dfrac{-6x}{-6}&& \\ \\ -3&\ge &x && \end{array}[/latex][latex]\text{Interval notation: } (-\infty, -3][/latex] Number line
  31. [latex]\begin{array}{rrrrrrr} \\ \\ \\ \\ \\ \\ \\ &&\dfrac{24+4b}{4}&<&\dfrac{4}{4}(1&+&6b) \\ \\ 6&+&b&<&1&+&6b \\ -1&-&b&&-1&-&b \\ \hline &&\dfrac{5}{5}&<&\dfrac{5b}{5}&& \\ \\ &&b&>&1&& \end{array}[/latex][latex]\text{Interval notation: } (1, \infty)[/latex] Number line
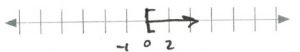
  32. [latex]\begin{array}{rrrrrrr} \\ \\ \\ -8(2&-&2n)&\ge &-16&+&n \\ -16&+&16n& \ge & -16 & + & n\\ +16&-&n&&+16 &-& n\\ \hline &&15n& \ge &0 &&\\ &&n& \ge &0 &&\\ \end{array}[/latex][latex]\text{Interval notation: } [0, \infty)[/latex] Number line
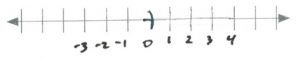
  33. [latex]\begin{array}{rrrrrrr} \\ \\ \\ \\ \\ \\ \\ &&\dfrac{-5v-5}{-5}&<&\dfrac{-5}{-5}(4v&+&1) \\ \\ v&+&1&>&4v&+&1 \\ -v&-&1&&-v&-&1 \\ \hline &&\dfrac{0}{3}&>&\dfrac{3v}{3}&& \\ \\ &&v&<&0&& \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 0)[/latex] Number line
  34. [latex]\begin{array}{rrrrrrrrr} \\ \\ \\ \\ \\ -36&+&6x&>&-8(x&+&2)&+&4x \\ -36&+&6x&>&-8x&-&16&+&4x \\ +16&-&6x&&-6x&+&16&& \\ \hline &&\dfrac{-20}{-10}&>&\dfrac{-10x}{-10}&&&& \\ \\ &&x&>&2&&&& \\ \end{array}[/latex][latex]\text{Interval notation: } (2, \infty)[/latex] Number line
  35. [latex]\begin{array}{rrrrrrrrl} \\ \\ \\ \\ 4&+&2(a&+&5)&<&-2(-a&-&4) \\ 4&+&2a&+&10&<&2a&+&8 \\ -4&-&2a&-&10&&-2a&-&10-4 \\ \hline &&0&<&-6&&&& \end{array}[/latex][latex]\text{False. No solution.}[/latex] Number line
  36. [latex]\begin{array}{rrrrrrrrrrrrr} \\ \\ \\ \\ \\ 3(n&+&3)&+&7(8&-&8n)&<&5n&+&5&+&2 \\ 3n&+&9&+&56&-&56n&<&5n&+&7&& \\ &&&&-53n&+&65&<&5n&+&7&& \\ &&&&-5n&-&65&&-5n&-&65&& \\ \hline &&&&&&-58n&<&-58&&&& \\ &&&&&&n&>&1&&&& \\ \end{array}[/latex][latex]\text{Interval notation: } (1, \infty)[/latex]
  37. [latex]\begin{array}{rrrrrrr} \\ \\ \\ -(k&-&2)&>&-k&-&20 \\ -k&+&2&>&-k&-&20 \\ +k&-&2&&+k&-&2 \\ \hline &&0&>&-22&& \\ \end{array}[/latex][latex]\text{Always true. Solution is all real numbers:} (-\infty, \infty)[/latex] Number line
  38. [latex]\begin{array}{rrrrrrrrl} \\ \\ \\ \\ -(4&-&5p)&+&3&\ge &-2(8&-&5p) \\ -4&+&5p&+&3&\ge &-16&+&10p \\ &&-1&+&5p&\ge &-16&+&10p \\ &&+1&-&10p&&+1&-&10p \\ \hline &&&&\dfrac{-5p}{-5}&\ge &\dfrac{-15}{-5}&& \\ \\ &&&&p&\le &3&& \\ \end{array}[/latex][latex]\text{Interval notation: } (-\infty, 3][/latex] Number line

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intermediate Algebra (Convert to MathJax) Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book