A rule of thumb about factoring: after spending several minutes trying to factor an equation, if its taking to long, use the quadratic equation to generate solutions instead.

Look at the equation [latex]ax^2 + bx + c = 0[/latex], the values of [latex]x[/latex] that make this equation equal to zero can be found by:

\[x=\dfrac{-b\pm (b^2-4ac)^{\frac{1}{2}}}{2a}\]

One of the key factors here is the value found from [latex](b^2 - 4ac)^{\frac{1}{2}}[/latex]. The interior of this radical [latex]b^2 - 4ac[/latex] can have three possible values: negative, positive, or zero.

[latex]b^2 - 4ac[/latex] is called the discriminant, and it defines how many solutions of [latex]x[/latex] there will be and what type of solutions they are.

If [latex]b^2 - 4ac = 0[/latex], then there is exactly one solution:

\[x=\dfrac{-b\pm 0}{2a}=\dfrac{-b}{2a}\]

The meaning of this is that the parabolic curve that can be drawn from the equation will only touch the [latex]x[/latex]-axis at one spot, and so there is only one solution for that quadratic. This can be seen from the image to the right: the quadratic curve touches the [latex]x[/latex]-axis at only one position, which means that there is only one solution for [latex]x[/latex].

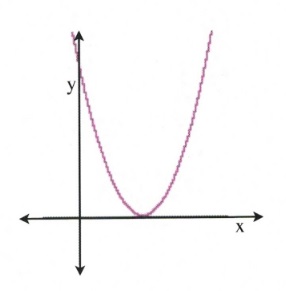
For example, the equation [latex]4x^2 + 4x + 1 = 0[/latex] has one solution. Check:

\[\begin{array}{rrrrrlll}
a=4\hspace{0.5in}&b^2&-&4ac&=&(4)^2&-&4(4)(1) \\
b=4\hspace{0.5in}&&&&=&16&-&16 \\
c=1\hspace{0.5in}&&&&=&0&&
\end{array}\]

The solution ends up being [latex]x = \dfrac{-(4)}{2(4)}[/latex] or [latex]x =-\dfrac{1}{2}[/latex].

If [latex]b^2 - 4ac =[/latex] any positive value, then there are exactly two solutions:

[latex]x=\dfrac{-b\pm \text{some positive number}}{2a}[/latex]

[latex]\text{or simply}[/latex]

[latex]\dfrac{-b+\text{some positive number}}{2a}\hspace{0.25in} \text{ and }\hspace{0.25in} \dfrac{-b-\text{ some positive number}}{2a}[/latex]

The meaning of this is that the parabolic curve that can be drawn from the equation will now touch (and cross) the [latex]x[/latex]-axis at two positions, and so there are now two solutions for the quadratic. This can be seen from the image to the right: the quadratic curve crosses the [latex]x[/latex]-axis at two positions, which means that there are now two solutions for [latex]x[/latex].

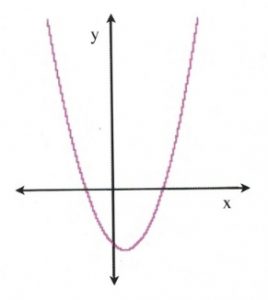
For example, the equation [latex]3x^2 + 4x + 1 = 0[/latex] has two solutions. Check:

\[\begin{array}{rrrrrlll}
a=3\hspace{0.5in}&b^2&-&4ac&=&(4)^2&-&4(3)(1) \\
b=4\hspace{0.5in}&&&&=&16&-&12 \\
c=1\hspace{0.5in}&&&&=&4&&
\end{array}\]

When 4 is put back into the quadratic equation and root 4 is taken, the solution now becomes ±2.

For this quadratic:

\[x=\dfrac{-4\pm 2}{2(3)}=\dfrac{-4\pm 2}{6}\]

The solutions are [latex]x = \dfrac{-6}{6}=-1[/latex] and [latex]x = \dfrac{-2}{6}=-\dfrac{1}{3}[/latex].

There exists one last possible solution for a quadratic, which happens when [latex]b^2 - 4ac =[/latex] any negative value. When this occurs, there are exactly two solutions, which are defined as imaginary roots or solutions or, more properly, complex roots, since the solution involves taking the root of a negative value.

The example provided shows that the quadratic never touches or crosses the [latex]x[/latex]-axis, yet it is possible to generate a solution if using imaginary numbers when solving a negative radical discriminant [latex]b^2 - 4ac[/latex].

For example, the equation [latex]5x^2 + 2x + 1 = 0[/latex] has two complex or imaginary solutions. Check:

\[\begin{array}{rrrrrcll}
a=5\hspace{0.5in}&b^2&-&4ac&=&(2)^2&-&4(5)(1) \\
b=2\hspace{0.5in}&&&&=&4&-&20 \\
c=1\hspace{0.5in}&&&&=&-16&&
\end{array}\]

When −16 is put back into the quadratic equation and the root of −16 is taken, the solution becomes [latex]\pm 4i[/latex].

For this quadratic:

\[x=\dfrac{-2\pm 4i}{2(5)}=\dfrac{-2\pm 4i}{10}\]

The solutions are [latex]x = \dfrac{-1+2i}{5}[/latex] and [latex]x = \dfrac{-1-2i}{5}[/latex].

Note: these solutions are complex conjugates of each other.

It is often useful to check the discriminants of a quadratic equation to define the nature of the roots for the quadratic before proceeding to a full solution.

In case you are curious:

How to Derive the Quadratic Formula

[latex]\begin{array}{rl} ax^2+bx+c=0&\text{Separate constant from variables} \\ -c-c& \text{Subtract }c\text{ from both sides} \\ \dfrac{ax^2}{a}+\dfrac{bx}{a}=\dfrac{-c}{a}&\text{Divide each term by }a \\ \\ x^2+\dfrac{b}{a}x=\dfrac{-c}{a}& \text{Find the number that completes the square}\\ \\ \left(\dfrac{1}{2}\cdot \dfrac{b}{a}\right)^2=\left(\dfrac{b}{2a}\right)^2=\dfrac{b^2}{4a^2}&\text{Add to both sides} \\ \\ \dfrac{b^2}{4a^2}-\dfrac{c}{a}\left(\dfrac{4a}{4a}\right)=\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}=\dfrac{b^2-4ac}{4a^2}&\text{Get the common denominator on the right} \\ \\ x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}=\dfrac{b^2-4ac}{4a^2}&\text{Factor} \\ \\ \left(x+\dfrac{b}{2a}\right)^2=\dfrac{b^2-4ac}{4a^2}&\text{Solve using the even root property} \\ \\ \sqrt{\left(x+\dfrac{b}{2a}\right)^2}=\pm \sqrt{\dfrac{b^2-4ac}{4a^2}}&\text{Simplify roots} \\ \\ x+\dfrac{b}{2a}=\dfrac{\pm \sqrt{b^2-4ac}}{2a}&\text{Subtract }\dfrac{b}{2a}\text{ from both sides} \\ \\ x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}&\text{Our solution} \end{array}[/latex]

Questions

Use the quadratic discriminant to determine the nature of the roots.

1. [latex]4x^2+2x-5=0[/latex]
2. [latex]9x^2-6x+1=0[/latex]
3. [latex]2x^2+3x-5=0[/latex]
4. [latex]3x^2+5x=3[/latex]
5. [latex]3x^2+5x=2[/latex]
6. [latex]x^2-8x+16=0[/latex]
7. [latex]a^2-56=-10a[/latex]
8. [latex]x^2+4=4x[/latex]
9. [latex]5x^2=-26+10x[/latex]
10. [latex]n^2=-21+10n[/latex]

Solve each of the following using the quadratic equation.

1. [latex]4a^2+3a-6=0[/latex]
2. [latex]3k^2+2k-3=0[/latex]
3. [latex]2x^2-8x-2=0[/latex]
4. [latex]6n^2+8n-1=0[/latex]
5. [latex]2m^2-3m+6=0[/latex]
6. [latex]5p^2+2p+6=0[/latex]
7. [latex]3r^2-2r-1=0[/latex]
8. [latex]2x^2-2x-15=0[/latex]
9. [latex]4n^2-3n+10=0[/latex]
10. [latex]b^2+6b+9=0[/latex]
11. [latex]v^2-4v-5=-8[/latex]
12. [latex]x^2+2x+6=4[/latex]

Answer Key 10.4